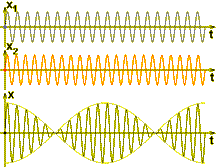
261. Dva harmonickΘ kmitavΘ pohyby blφzkych frekvenciφ sa skladaj· do v²slednΘho pohybu, ktor² sa vyznaΦuje 5 rßzmi za sekundu. Akß je frekvencia druhΘho z t²chto pohybov, ke∩ prv² mß frekvenciu f1 = 40 s-1?
 |
|
fr = 5 s-1, f1 = 40 s-1, f2 = ? |
|
Pre jednoduchos¥ budeme uva₧ova¥ kmitavΘ pohyby s rovnak²mi amplit·dami x0 a fßzov²mi konÜtantami pohybu j . Pre v²chylky z rovnovß₧nych pol⌠h pohybov platφ:
,
(1)
.
(2)
Vyu₧itφm vlastnostφ goniometrick²ch funkciφ pre v²chylku v²slednΘho pohyb x zlo₧enΘho z dvoch kmitav²ch pohybov x1 a x2 dostaneme:
,
(3)
priΦom prvß Φas¥ v²slednΘho vz¥ahu charakterizuje amplit·du pohybu a druhß Φas¥ predstavuje fßzu pohybu. Pre peri≤du v²slednΘho pohybu m⌠₧eme teda pφsa¥:
.
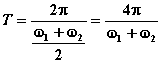(4)
Amplit·da v²slednΘho pohybu sa s Φasom menφ periodicky a pre peri≤du jej zmeny platφ:
.
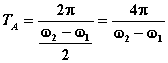(5)
Ke∩₧e za jednu peri≤du zmeny amplit·dy vznikn· dve zosilnenia a dve zoslabenia, t.j. rßzy, pre peri≤du rßzov platφ:
(6)
a pre v²sledn· frekvenciu rßzov m⌠₧eme teda pφsa¥:
(7)
Pre h╛adan· frekvenciu f2 teda platφ:
(8)
.
Vzh╛adom k vlastnostiam funkcie kosφnus m⌠₧e ma¥ ·loha aj druhΘ rieÜenie. Ke∩₧e je kosφnus pßrna funkcia a platφ:
(9)
m⌠₧e nasta¥ aj situßcie, ₧e frekvencia druhΘho z pohybov bude menÜia ako frekvencia prvΘho. Potom analogickou ·pravou predchßdzaj·cich vz¥ahov by sme sa dopracovali aj k ∩alÜiemu rieÜeniu:
(10)
a pre h╛adan· frekvenciu f2 by platilo:
(11)
.
Frekvencia druhΘho z t²chto pohybov je 45 s-1 (35 s-1).
Pohyb
hmotnΘho bodu po kru₧nici
