|

|
|
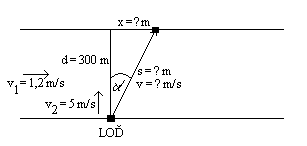
59. V rieke širokej 300 metrov tečie voda rýchlosťou
veľkosti 1,2 m/s. Loď sa pohybuje vzhľadom na vodu rýchlosťou veľkosti
5 m/s. V akom smere sa má pohybovať loď, keď sa má dostať na druhý
breh za najkratší čas a aký je tento čas? O koľko sa odkloní od svojho
pôvodného smeru?
|
|
| |
|
|
|
|
|
|
|
|
d
= 300 m
v1
= 1,2 m/s
v2
= 5 m/s
t
= ? s, a
= ? °
|
 |
|
|
| |
|
Celkový
pohyb lode vzhľadom k vzťažnej sústave spojenej so Zemou je zložený
z dvoch pohybov – z vlastného pohybu lode a z unášavého
pohybu vody. Keby
sa loď pohybovala v nehybnej vode, musela by ísť od jedného brehu po
druhý kolmo na breh, aby jej to trvalo najkratší čas. Dráhu
d = 300 m by prešla za čas t
:
|
|
| |
|
|
t
= d / v
t
= 300 m / (5 m/s)
t
= 60 s .
|
(1)
|
|
| |
|
Keďže
sa loď pohybuje v prúdiacej rieke a poznáme obe zložky jej celkovej
rýchlosti v, využitím Pytagorovej vety dostaneme veľkosť
rýchlosti v lode vzhľadom na breh:
|
|
| |
|
|
v =
(v12 + v22)1/2
.
|
(2)
|
|
| |
|
Uhol
odklonu lode od pôvodného smeru zistíme pomocou goniometrických funkcií:
|
|
| |
|
|
tga
= v1 / v2 =
x / d
tga
= 0,24
a
= 13,5 ° .
|
|
|
| |
|
Pre dráhu x
platí:
|
|
|
|
| |
|
|
x
= tga
d
.
|
|
|
| |
|
Celkovú
prejdenú dráhu s lode vypočítame pomocou Pytagorovej
vety:
|
|
| |
|
|
s
= (d2 + x2)1/2 .
|
(3)
|
|
| |
|
Využitím
vzťahu pre veľkosť dráhy rovnomerného priamočiareho pohybu zistíme čas
t, za ktorý sa loď skutočne dostane na druhý breh:
|
|
| |
|
|
s
= vt
t
= s / v
t
= (3002 + 722)1/2 m /
(1,22 + 52)1/2 m/s
t
= 308,52 m / 5,14 m/s
t
= 60 s .
|
(4)
|
|
| |
|
Zistili
sme, že ide o rovnaký čas ako v prípade nehybnej vody, lebo je to najkratší
možný čas, za ktorý sa loď dostane na druhý breh.
|
|
| |
|
|
|
| |
|
Loď
sa má pohybovať v smere kolmom na prúd rieky. Vtedy jej pohyb bude
trvať 60 sekúnd a od pôvodného smeru sa odkloní o 13,5 °.
|
|
| |
|
|
|
| |
|
 Zvislý
vrh nahor a nadol Zvislý
vrh nahor a nadol
 Balistické
kyvadlo Balistické
kyvadlo
 Koeficient
tlmenia Koeficient
tlmenia
|
|
| |
|
|
|
 |
|

|
 |