129. - BalistickΘ kyvadlo

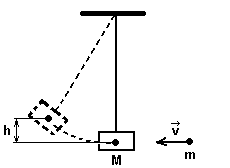
129. Do akej v²Üky sa vych²li balistickΘ kyvadlo hmotnosti 10 kg, ke∩ v ≥om uviazne strela hmotnosti 100 g letiaca r²chlos¥ou 200 m/s ?

M = 10 kg

m = 100 g =>

m = 0,1 kg

v = 200 m.s^-1

g = 9,81 m.s^-2

h = ?

Pri zasiahnutφ kyvadla strelou sa Φas¥ kinetickej energie gu╛⌠Φky premenφ na vn·torn· energiu kyvadla. V tomto prφpade sa nedß pou₧i¥ pre s·stavu strela-kyvadlo zßkon zachovania mechanickej energie (ZZE), preto₧e ve╛kß Φas¥ kinetickej energie strely sa po vniknutφ do kyvadla spotrebuje na teplo, tak₧e nedochßdza tu k premene kinetickej energie strely na polohov· energiu kyvadla. Vyjdeme teda zo zßkona zachovania hybnosti izolovanej s·stavy (ZZH). Zo ZZH vypl²va:

p = p^' ,

(1)

mv = (m + M)v^' ,

priΦom m je hmotnos¥ strely, M hmotnos¥ kyvadla, v je r²chlos¥ strely a v^' je v²slednß r²chlos¥ s·stavy kyvadlo-strela tesne po zrß₧ke. Dostßvame:

v^'= mv / (m + M) .

Ke∩₧e pri pohybe s·stavy kyvadlo-strela u₧ neuva₧ujeme straty energie, m⌠₧eme pou₧i¥ ZZE. Celkovß kinetickß energia s·stavy po zasiahnutφ strelou sa pod╛a zßkona zachovania mechanickej energie musφ rovna¥ celkovej potencißlnej energii s·stavy pri jej maximßlnom vych²lenφ, teda:

1/2 (m + M)v^'2= (m + M)gh

(2)

v^'2= 2gh
m²v²/ (m + M)²= 2gh
m²v²/ 2g(m + M)² = h .

StaΦφ u₧ len dosadi¥ hodnoty zo zadania a dostßvame:

h = 0,2 m .

BalistickΘ kyvadlo sa vych²li do v²Üky 0,2 metra.

Priemernß r²chlos¥ cyklistu

Zvisl² vrh nahor a nadol

Odraz gu╛⌠Φky