291. HomogΘnna ₧eleznß tyΦ s hmotnos¥ou m = 3 kg mß pri teplote 8 ░C dσ₧ku 1 meter. VypoΦφtajte, ako sa zmenφ moment zotrvaΦnosti tejto tyΦe vzh╛adom na os kolm· na smer tyΦe a prechßdzaj·cu jej koncov²m bodom, ke∩ sa zohreje na teplotu 100 ░C.

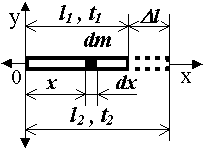
Moment zotrvaΦnosti homogΘnnej tyΦe vzh╛adom na os prechßdzaj·cu jej koncov²m bodom a kolm· na smer tyΦe vypoΦφtame pod╛a vz¥ahu:

J = ≥  x² dm  .

(1)

Ke∩₧e si element hmotnosti m⌠₧eme vyjadri¥ cez element dσ₧ky:

dm = (m / l) dx  ,

(2)

potom pre moment zotrvaΦnosti tyΦe vzh╛adom na dan· os m⌠₧eme pφsa¥: 

J = m / l  ≥  x² dx

J = m / l  [x³ / 3]₀^l

J = 1/3 ml²  .

(3)

Pre zmenu momentu zotrvaΦnosti po predσ₧enφ tyΦe platφ:

DJ=  J₂ û J₁  ,

(4)

kde

J₂ = 1/3 ml₂²  a  J₁ = 1/3 ml₁²  ,

priΦom

l₂ = l₁(1 + a Dt)  .

(5)

Vyu₧itφm dan²ch vz¥ahov pre zmenu momentu zotrvaΦnosti dostaneme:

DJ =  1/3 ml₁² ((1 + a Dt)² û 1)  .

Po dosadenφ hodn⌠t zo zadania dostßvame:

DJ = 1/3 . 3 kg . (1 m)² . ((1 + 12 . 10 ^-6 K^-1 . 92 K)² - 1)  

DJ = 22 . 10^-4 kg.m²  .

Moment zotrvaΦnosti tyΦe vzh╛adom na os kolm· na smer tyΦe a prechßdzaj·cu jej koncov²m bodom sa po jej predσ₧enφ zvΣΦÜφ pribli₧ne o 22 . 10^-4 kg.m².

Stavovß rovnica ideßlneho plynu