|

|
|
27.
Pohyb
bodu je daný v polárnych súradniciach
rovnicami r
= n . t, j
= b . t, kde n a b sú konštanty. Nájdite rovnicu dráhy pohybu a vyjadrite
závislosť rýchlosti a zrýchlenia od času!
|
|
| |
|
|
|
|
|
|
n,
b
r
= n . t
j
= b . t
v
= ?, a = ?
|
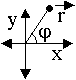
|
|
|
| |
|
|
|
| |
|
Pohyb
bodu je vyjadrený rovnicami:
|
|
| |
|
|
r
= nt ,
|
(1)
|
|
| |
|
|
j
= bt
.
|
(2)
|
|
| |
|
Keď
si z predchádzajúcej rovnice (2) vyjadríme čas t
a dosadíme do rovnice (1), dostaneme rovnicu dráhy pohybu
bodu:
|
|
| |
|
|
r
= n / b j
.
|
(3)
|
|
| |
|
Pohyb
bodu v rovine možno okrem karteziánskych súradníc x, y
opísať aj dvojicou krivočiarych - polárnych súradníc r,
j.
Medzi karteziánskymi a polárnymi súradnicami existuje vzájomne jednoznačné
priradenie vyjadrené rovnicami:
|
|
| |
|
|
x
= r cos j
,
|
(4)
|
|
| |
|
|
y
= r sin j
,
|
(5)
|
|
| |
|
pričom
|
|
| |
|
|
r
= (x2 + y2)1/2 .
|
(6)
|
|
| |
|
Dosadením
pôvodných vzťahov r = nt, j
= bt do
predchádzajúcich rovníc (4) a (5) dostávame
súradnice polohy bodu v čase t:
|
|
| |
|
|
x
= nt cos bt ,
|
(7)
|
|
| |
|
|
y =
nt sin bt .
|
(8)
|
|
| |
|
Zderivovaním
vzťahov (7), (8) podľa času dostaneme rovnice
rýchlosti vx a vy:
|
|
| |
|
|
vx
= dx / dt = n cos bt + nt (-sin bt)
b ,
|
(9)
|
|
| |
|
|
vy
= dy / dt = n sin bt + nt cos bt b
.
|
(10)
|
|
| |
|
Druhou deriváciou
polohy bodu podľa času dostaneme vzťahy pre zrýchlenia ax,
ay v daných smeroch:
|
|
| |
|
ax
= d2x / dt2 = n (-sin bt)
b + n (-sin bt) b - nt cos bt b2
,
(11)
|
|
| |
|
ax
= -2n sin bt b - nt cos bt b2
,
(12)
|
|
| |
|
ay
= d2y
/ dt2 = n
cos bt b + n cos bt b + nt (-sin bt) b2
,
(13)
|
|
| |
|
ay
= 2n cos bt b - nt sin bt b2
.
(14)
|
|
| |
|
Pre hodnotu celkovej
rýchlosti v hmotného bodu platí:
|
|
| |
|
|
v
= {vx2 + vy2}1/2
|
(15)
|
|
| |
|
v
= {[n cos bt - nt sin bt b]2 + [n sin
bt + nt cos bt b]2}1/2 =
=
{(n cos
bt)2 - 2n cos bt nt sin bt b + (nt sin
bt b)2 +
+
(n sin bt)2 + 2n sin bt nt cos bt b
+ (nt cos bt b)2}1/2
=
=
{(n cos bt)2 + (nt sin bt b)2 +
(n sin bt)2 + (nt cos bt b)2}1/2=
=
{n2[cos2 bt
+ sin2 bt
] + n2t2b2[sin2
bt + cos2 bt
]}1/2
=
=
{n2
+ n2t2b2}1/2 =
{n2(1+ t2b2)}1/2 =
n{1+ t2b2}1/2
.
|
|
| |
|
|
v
=
n {1 + t2b2}1/2
.
|
(16)
|
|
| |
|
Pre celkové zrýchlenie a platí:
|
|
| |
|
|
a
= {ax2 + ay2}1/2
|
(17)
|
|
| |
|
a
= {[-2n sin
bt b - nt cos bt b2]2 + [2n cos
bt b - nt sin bt b2]2}1/2=
=
{4n2 sin2 bt b2 + 4n sin
bt bnt cos bt b2 +
n2t2
cos2 bt
b4 +
+ 4n2 cos2 bt b2
- 4n cos bt bnt sin bt b2 + n2t2
sin2 bt
b4}1/2 =
=
{4n2b2[cos2
bt + sin2
bt] + n2t2b4[cos2
bt + sin2
bt]}1/2 =
=
{ 4n2b2 + n2t2b4}1/2
= {n2b2(4
+ t2b2)}1/2 =
nb{4 + t2b2}1/2
|
|
| |
|
|
a
=
nb
{4 + t2b2}1/2
.
|
(18)
|
|
| |
|
|
|
| |
|
Dráha
je Archimedova špirála s rovnicou:
r = ( n /
b ) j
.
Rýchlosť
bodu je
v = n (1 + t2b2)1/2 a jeho
zrýchlenie a = nb
(4 + t2b2)1/2.
|
|
| |
|
|
|
| |
|
 Druhá
kozmická rýchlosť Druhá
kozmická rýchlosť
 Balistické
kyvadlo Balistické
kyvadlo
 Dopplerov
princíp Dopplerov
princíp
|
|
| |
|
|
|
 |
|

|
 |