Iterßtory II. Bez koncept∙ ani rßnu...

Prvnφ dφl mßme za sebou, tΘmatem dne jsou koncepty. Probereme si koncepty iterßtor∙ pou₧itΘ ve standardnφ knihovn∞ STL jazyka C++.

Motivace

R∙znΘ kontejnery poskytujφ iterßtory r∙znΘ kvality. Nap°. klasickΘ pole nebo t°φda vector umo₧≥ujφ snadno, v konstantnφm Φase, zφskat iterßtor na libovoln² prvek û staΦφ znßt jeho index. U seznamu (t°φda list) je situace slo₧it∞jÜφ. Kdy₧ chceme k-t² prvek, musφme jφt na zaΦßtek seznamu a provΘst k iteracφ, abychom se k n∞mu dostali.

To samΘ platφ pro algoritmy: r∙znΘ algoritmy vy₧adujφ iterßtory r∙znΘ kvality. Vezm∞me si t°eba jednoduch² v²poΦet aritmetickΘho pr∙m∞ru a sm∞rodatnΘ odchylky.

 

template <typename ITERATOR>

double prumer(ITERATOR prvni, ITERATOR posledni)

{

áá double avg = 0.0;

 

áá std::size_t pocet = 0;

áá while ( prvni != posledni )

áá {

ááááá avg += *prvni++;

ááááá ++pocet;

áá }

 

áá if ( pocet > 0 )

áá {

ááááá avg /= static_cast<double>(pocet);

áá }

 

áá return avg;

}

 

Jak je vid∞t, staΦφ nßm jeden pr∙chod p°es zadan² rozsah. To znamenß, ₧e vstupnφ data mohou pochßzet jak z pole, vektoru, seznamu, tak i t°eba ze vstupnφho datovΘho proudu (nap°. vstup z p°φkazovΘ °ßdky). Nynφ jak vypadß sm∞rodatnß odchylka

 

template <typename ITERATOR>

double odchylka(ITERATOR prvni, ITERATOR posledni)

{

áá double avg = 0.0;

áá double var = 0.0;

áá ITERATOR i(prvni);á // ulo₧it prvni

 

áá // prvnφ pr∙chod

áá std::size_t pocet = 0;

áá while ( prvni != posledni )

áá {

ááááá avg += *prvni++;

ááááá ++pocet;

áá }

 

áá if ( pocet > 0 )

áá {

ááááá avg /= static_cast<double>(pocet);

ááááá double sum = 0.0;

 

ááááá // druh² pr∙chod

ááááá while ( i != posledni )

ááááá {

áááááááá double tmp = *i++ - avg;

áááááááá sum += tmp;

áááááááá var += tmp * tmp;

ááááá }

 

ááááá // korekce :

ááááá var = (var - sum * sum /

áááááááááááá static_cast<double>(pocet)) / (pocet - 1);

áá }

 

áá return sqrt(var);

}

 

Tento algoritmus je u₧ dvoupr∙chodov²: v prvnφm pr∙chodu p°es zadan² rozsah se spoΦte aritmetick² pr∙m∞r a ten je pak pou₧it v druhΘm pr∙chodu k v²poΦtu standardnφ odchylky. To znamenß, ₧e tento algoritmus vy₧aduje vφc od äsvΘhoô iterßtoru (konkrΘtn∞ mo₧nost vφce pr∙chod∙ p°es zadan² rozsah). Tak₧e u₧ nejde pou₧φt vstup p°φmo z p°φkazovΘ °ßdky, proto₧e tento je pouze jednopr∙chodov² (jako data na pßsce, kterß se posunuje jen jednφm sm∞rem û dovnit°).

DalÜφm zajφmav²m momentem je t°φd∞nφ. T°φdit lze i s  vφcepr∙chodov²mi ukazateli, ale nemusφ to b²t efektivnφ. T∞₧ko si lze p°edstavit algoritmus quicksort, kter² by pro ka₧d² p°φstup k jakΘmukoliv prvku musel jφt na zaΦßtek rozsahu a odpoΦφtat pot°ebn² poΦet iteracφ k danΘmu prvku (p°φstup ke k-tΘmu prvku by vy₧adoval k iteracφ, zde by bylo na mφst∞ spφÜe pojmenovßnφ slowsort). ╪eÜφ to dodateΦnΘ po₧adavky na iterßtor: pokud iterßtor umo₧≥uje nßhodn² p°φstup (p°φstup ke k-tΘmu prvku v konstantnφm Φase), m∙₧e b²t t°φd∞nφ implementovßno velmi efektivn∞. Zde se st°etßvajφ dv∞ pravidla:

Pokud pou₧ijeme obecn∞jÜφ vφcepr∙chodov² iterßtor, nebude t°φd∞nφ efektivnφ. A naopak, p°i pou₧itφ iterßtor∙ s nßhodn²m p°φstupem bude t°φd∞nφ efektivnφ, ale nedokß₧u set°φdit vÜechno, proto₧e ne vÜechny kontejnery poskytujφ iterßtory s nßhodn²m p°φstupem. Vφt∞zφ efektivita û t°φdφcφ algoritmy vy₧adujφ iterßtory s nßhodn²m p°φstupem. A kdy₧ to nejde jinak, je v₧dy mo₧no doprogramovat t°φd∞nφ pro obecn∞jÜφ iterßtory bez nßhodnΘho p°φstupu. Proto takΘ t°φda list kterΘ se to t²kß, mß vlastnφ optimalizovanou metodu pro set°φd∞nφ dat.

Co z toho vÜeho plyne? Iterßtory je mo₧nΘ kategorizovat podle toho, jak p°istupujφ k prvk∙m, jestli jsou jednopr∙chodovΘ nebo vφcepr∙chodovΘ, nebo nap°. jestli je mo₧nΘ iterovat jen jednφm sm∞rem nebo i zpßtky.

Na Obr. 1 vidφme hierarchii koncept∙ iterßtor∙ v STL. èipky naznaΦujφ zjemn∞nφ konceptu. Analogicky jako p°i d∞d∞nφ v duchu OOP: Tam, kde se oΦekßvß n∞jak² koncept, funguje i jeho zjemn∞nφ.

 

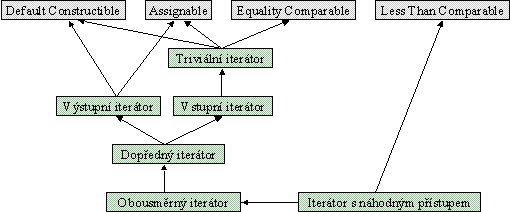
Obr. 1 Hierarchie koncept∙

Primitivnφ koncepty

Nejd°φve si pro ·plnost vysv∞tlφme v²znam Φty° primitivnφch koncept∙, kterΘ jsou na Obr. 1 barevn∞ odliÜeny od koncept∙ iterßtor∙.

Default Constructible

Typy umo₧≥ujφcφ implicitnφ inicializaci, tj. jak²koliv vestav∞n² typ nebo t°φda s ve°ejn∞ p°φstupn²m implicitnφm konstruktorem. Tato inicializace nemusφ objektu p°i°adit ₧ßdnou konkrΘtnφ hodnotu. V p°φpad∞ iterßtor∙ jde o vytvo°enφ singulßrnφ hodnoty (neinicializovan² iterßtor).

Assignable

Typy, jejich₧ instance se chovajφ jako (ΦφselnΘ) hodnoty. Instance je mo₧nΘ kopφrovat (kopφrovacφ konstruktor) a p°i°azovat (operßtor =). Pat°φ sem samoz°ejm∞ takΘ vÜechny vestav∞nΘ typy.

Equality Comparable

Typy, jejich₧ instance lze porovnßvat operßtory == a !=. SΘmantika by m∞la odpovφdat relacφm rovnosti a nerovnosti znßm²m ze zßkladnφho kurzu matematiky.

Less Than Comparable

Typy, pro n∞₧ jsou definovßny relaΦnφ operßtory <, >, <=, >=, od kter²ch se oΦekßvß stejnß sΘmantika, jako u odpovφdajφcφch relacφ, kterΘ znßte ze zßkladnφ v²uky matematiky.

Trivißlnφ iterßtor

ZjednoduÜen∞ °eΦeno, trivißlnφ iterßtor je takov² iterßtor, kter² odkazuje na n∞jak² prvek, ale neumo₧≥uje p°echod na jin² prvek. Tento koncept je vφcemΘn∞ teoretickß zßle₧itost, nebo¥ generickΘ algoritmy pracujφ v₧dy s n∞jak²m rozsahem prvk∙ a pou₧φvajφ iterßtory pro pohyb mezi prvky.

Modelem m∙₧e b²t nap°φklad ukazatel na objekt, kter² nenφ souΦßstφ pole. Z pohledu C++ vÜak nedokß₧eme rozliÜit, jestli ukazatel ukazuje na prvek v poli, nebo na osamocen² prvek mimo pole

 

int * prvek = new int (0);á // osamocen² prvek

int * pole = new int [20];á // pole

 

int neco = prvek[0];á // tohle projde i kdy₧ nejde o pole

int takyneco = *pole;á // tohle je b∞₧nß konstrukce

 

Trivißlnφ iterßtor podporuje vÜechny operace äzd∞d∞nΘô od koncept∙, kterΘ zjem≥uje, a navφc jeÜt∞ podporuje dereferencovßnφ operßtorem *, zm∞nu prvku a p°φstup ke slo₧kßm prvku (pokud je prvek instance n∞jakΘ t°φdy) pomocφ operßtoru ->, viz tabulka 1. U trivißlnφho iterßtoru mß smysl mluvit o typu prvku.

 

operace

zßpis

poznßmky

dereferencovßnφ

*i

i je dereferencovatelnß hodnota.

zm∞na prvku

*i = b

i je dereferencovatelnß hodnota a nekonstantnφ iterßtor; b je hodnota (instance) stejnΘho typu jako typ prvku iterßtoru i.

p°φstup ke slo₧kßm prvku

i->slozka

Pokud je odkazovan² prvek t°φda je mo₧nΘ p°istupovat k jeho slo₧kßm pomocφ p°etφ₧enΘho operßtoru ->. Ekvivalentnφ zßpis je (*i).slozka. i je dereferencovatelnß hodnota

 

Tab. 1 Trivißlnφ iterßtor û co p°idßvß k zjem≥ovan²m primitivnφm koncept∙m. VÜechny tyto operace majφ konstantnφ Φasovou slo₧itost.

Vstupnφ iterßtor

NejjednoduÜÜφm äb∞₧n²mô iterßtorem, je tzv. vstupnφ iterßtor. Jednß se o zjemn∞nφ konceptu trivißlnφho iterßtoru. Zjemn∞nφ se t²kß nßsledujφcφch vlastnostφ:

NejjednoduÜÜφm modelem je samoz°ejm∞ klasick² ukazatel do pole prvk∙. Ukß₧eme si dßle, ₧e klasickΘ ukazatele podporujφ mnohem vφce, ne₧ jen koncept vstupnφho iterßtoru.

Jin²m modelem, kter² nenφ v∙bec zalo₧en na pou₧itφ ukazatele, je iterßtor na vstupnφm datovΘm proudu istream_iterator (o n∞m si povφme vφce p°φÜt∞). Tento iterßtor je, narozdφl od ukazatele, nanejv²Ü vstupnφ a nenφ modelem ₧ßdnΘho dalÜφho zjemn∞nφ, nap°. dop°ednΘho iterßtoru.

Ke vstupnφmu iterßtoru pat°φ typ prvku a typ rozdφlu (vzdßlenost mezi iterßtory nebo poΦet prvk∙ v rozsahu).

 

operace

zßpis

poznßmky

p°echod na dalÜφ prvek

++i

i je dereferencovatelnß hodnota; v²sledkem m∙₧e b²t iterßtor na prvnφ (neexistujφcφ) prvek za koncem kontejneru.

p°echod na dalÜφ prvek

i++

i je dereferencovatelnß hodnota, ekvivalentnφ s ++i

p°φstup k prvku a p°echod na dalÜφ prvek

*i++

i je dereferencovatelnß hodnota. Ekvivalentnφ s

{ TYP a = *i; ++i; return a; }.

 

Tab. 2 Operace, kterΘ zavßdφ vstupnφ iterßtor. VÜechny tyto operace majφ konstantnφ Φasovou slo₧itost.

 

Kdy₧ se vrßtφme k ·vodnφ funkci pro v²poΦet aritmetickΘho pr∙m∞ru, je jist∞ jasnΘ, ₧e v²stupnφ iterßtor je tφm nejobecn∞jÜφm iterßtorem, pro kter² lze danou funkci napsat (ani₧ by utrp∞la efektivita algoritmu). Jedinou mo₧nostφ, jak v C++ tuto skuteΦnost vyjßd°it, je pojmenovßnφ ÜablonovΘho parametru, nap°φklad takto

 

template <typename VSTUPNI_ITERATOR>

double prumer(VSTUPNI_ITERATOR prvni, VSTUPNI_ITERATOR posledni);

 

nebo ve stylu STL takto

 

template <typename InputIterator>

double prumer(InputIterator prvni, InputIterator posledni);

V²stupnφ iterßtor

Zdßlo by se, ₧e v²stupnφ iterßtor je opakem vstupnφho iterßtoru, ale situace je pon∞kud slo₧it∞jÜφ. Jak nßzev napovφdß, v²stupnφ iterßtor je urΦen pro uklßdßnφ sekvencφ hodnot än∞kamô. Nemusφ vÜak podporovat p°φstup k t∞mto hodnotßm, tj. ani p°φstup k jejich slo₧kßm pomocφ operßtoru ->, a ani relaci rovnosti (iterßtor∙). Proto tento koncept neznß typ prvku ani typ rozdφlu. Umφ vÜak p°echod na dalÜφ prvek.

Zkuste si to p°edstavit nap°φklad jako magnetick² pßsek (kontejner) a zapisovacφ hlavu (iterßtor). M∙₧eme zapsat data a posunout pßsek na dalÜφ volnou pozici, ale nem∙₧eme ty data z pßsku Φφst ani se vrßtit zpßtky (p°evinout pßsku zp∞t). P°esn∞ tato p°edstava odpovφdß jednomu konkrΘtnφmu modelu, iterßtoru na v²stupnφm proudu û t°φd∞ ostream_iterator.

Klasick² ukazatel je rovn∞₧ modelem v²stupnφho iterßtoru (i kdy₧ toho umφ mnohem vφc).

 

operace

zßpis

poznßmky

dereference a ulo₧enφ prvku

*i = a

i je dereferencovatelnß hodnota, a je hodnota n∞jakΘho (vhodnΘho) typu. Mezi dv∞ma t∞mito operacemi musφ prob∞hnout p°echod na dalÜφ prvek.

p°echod na mφsto k ulo₧enφ dalÜφho prvku

++i

i je dereferencovatelnß hodnota. P°edtφm muselo prob∞hnout p°i°azenφ do *i.

p°echod na mφsto k ulo₧enφ dalÜφho prvku

i++

i je dereferencovatelnß hodnota. P°edtφm muselo prob∞hnout p°i°azenφ do *i.

ulo₧enφ prvku a p°echod na mφsto k ulo₧enφ dalÜφho prvku

*i++ = a

i je dereferencovatelnß hodnota, a je hodnota n∞jakΘho (vhodnΘho) typu. Ekvivalentnφ s

{ *i = a; ++i; }.

 

Tab. 3 Operace, kterΘ zavßdφ v²stupnφ iterßtor. VÜechny majφ konstantnφ Φasovou slo₧itost.

 

JeÜt∞ n∞kolik d∙le₧it²ch poznßmek k p°i°azenφ *i = a. Za prvΘ, konstantnφ Φasovß slo₧itost je vzta₧ena k operaci s iterßtorem, vlastnφ ulo₧enφ prvku m∙₧e mφt jinou Φasovou slo₧itost. Za druhΘ, operßtor p°i°azenφ lze ve v²stupnφm iterßtoru p°etφ₧it tak, aby vracel proxy, neboli zßstupnou t°φdu, kterß rovn∞₧ musφ mφt p°etφ₧en² operßtor p°i°azenφ. Ptßte se, k Φemu je to dobrΘ? Vypadß to jako zbyteΦnß komplikace, ale je v tom skryt velmi siln² aparßt. Kdy₧ toti₧ v proxy p°etφ₧φme operßtor p°i°azenφ pro r∙znΘ typy nebo dokonce vytvo°φme Φlenskou Üablonu operßtoru p°i°azenφ parametrizovanou typem v²stupnφ hodnoty, m∙₧eme pomocφ v²stupnφho iterßtoru s proxy uklßdat hodnoty vφce typ∙. To proto nemß smysl uva₧ovat (pevn²) typ prvku pro v²stupnφ iterßtory. O v²stupnφch iterßtorech a proxy toho jeÜt∞ hodn∞ uslyÜφte.

NemΘn∞ d∙le₧itou vlastnostφ je vztah p°i°azenφ a p°echodu na dalÜφ prvek. Nelze dvakrßt zapsat na jedno mφsto. Mezi dv∞ma zßpisy musφ prob∞hnout p°echod na dalÜφ prvek. Po p°echodu na dalÜφ prvek m∙₧e nßsledovat zßpis (p°i°azenφ) ale nikoli dalÜφ p°echod.

 

// Koncept: Vystupni iterator

*i = 1; ++i; *i = 2;áááá // OK

*i++ = 1; *i++ = 2;áááá // OK

*i = 1; *i = 2;áááá // !! Nelze

*i++ = 1; ++i; *i=2;áááá // !! Nelze

 

Takhle n∞jak se chovß t°φda ostream_iterator. KlasickΘ ukazatele vßm sice umo₧nφ provΘst vÜechny Φty°i °ßdky, ale to je tφm, ₧e ukazatel je rovn∞₧ modelem mnohem pokroΦilejÜφho konceptu, ne₧ je v²stupnφ iterßtor.

Dop°edn² iterßtor

KoneΦn∞ jsme dosp∞li k prvnφmu änormßlnφmuô iterßtoru. Dop°edn² iterßtor umo₧≥uje Φφst i zapisovat prvky, prochßzet mezi prvky (pouze v jednom sm∞ru) a navφc je zaruΦena mo₧nost opakovanΘho pr∙chodu (to vstupnφ ani v²stupnφ iterßtor negarantujφ). Je tedy mo₧nΘ ulo₧it si kopii iterßtoru, nap°. na zaΦßtek rozsahu, a projφt dan² rozsah jeÜt∞ jednou.

Koncept dop°ednΘho iterßtoru je zjemn∞nφm koncept∙ vstupnφho a v²stupnφho iterßtoru. Nezavßdφ vÜak dalÜφ novΘ operace; pouze odstra≥uje n∞kterß omezenφ. Nap°φklad p°i p°echodu z i do ++i mß iterßtor i zaruΦenu platnost. Je tedy mo₧nΘ se do tohoto mφsta vrßtit a znovu jφm projφt. To je zßkladnφ p°edpoklad pro vφcepr∙chodovΘ algoritmy. Navφc pokud i == j, pak ++i == ++j (To v p°φpad∞ vstupnφch a v²stupnφch iterßtor∙ neplatilo).

Modelem je zcela jist∞ klasick² ukazatel. DalÜφm modelem m∙₧e b²t t°eba iterßtor na seznamu (list<T>::iterator), vektoru a jin²ch STL kontejnerech.

Pokud se vrßtφme na zaΦßtek k funkci odchylka, zjistφme, ₧e dop°edn² iterßtor je p°esn∞ to, co pot°ebujeme. Vyjßd°φme tuto skuteΦnost pojmenovßnφm ÜablonovΘho parametru

 

template <typename DOPREDNY_ITERATOR>

double odchylka(DOPREDNY_ITERATOR prvni, DOPREDNY_ITERATOR posledni);

 

nebo ve stylu STL

 

template <typename ForwardIterator>

double odchylka(ForwardIterator prvni, ForwardIterator posledni);

Obousm∞rn² iterßtor

Nastal Φas p°idat zp∞tn² chod, tj. umo₧nit iterßtoru p°ejφt jak na nßsledujφcφ, tak na p°edchßzejφcφ prvek. Koncept obousm∞rnΘho iterßtoru zjem≥uje koncept dop°ednΘho iterßtoru. P°idßvß jen p°etφ₧en² operßtor -- pro zp∞tn² chod. P°itom operace ++ a -- musφ b²t symetrickΘ, tj. ob∞ dv∞ nßsledujφcφ sekvence

 

++i; --i;

--i; ++i;

 

p°edstavujφ nulovou operace, tj. äjako by se nic nestaloô.

Modelem je op∞t klasick² ukazatel, iterßtor na seznamu (standardnφ t°φda list je implementovßna jako obousm∞rn² seznam), nebo iterßtor na vektoru.

 

operace

zßpis

poznßmky

p°echod na p°edchozφ prvek

--i

i je dereferencovatelnß hodnota.

p°echod na p°edchozφ prvek

i--

i je dereferencovatelnß hodnota, ekvivalentnφ s { TYP tmp = i; --i; return tmp }, kde TYP je typ iterßtoru.

 

Tab. 4 Operace pro zp∞tn² chod u obousm∞rnΘho iterßtoru (op∞t konstantnφ slo₧itost).

Iterßtor s nßhodn²m p°φstupem

Dostßvßme se k nejpokroΦilejÜφmu konceptu iterßtoru. Iterßtor s nßhodn²m p°φstupem umφ vÜe co obousm∞rn² iterßtor a navφc garantuje p°φstup v konstantnφm Φase k jakΘmukoliv prvku v danΘm rozsahu. Tφm pßdem umo₧≥uje v konstantnφm Φase posuny vp°ed a vzad o libovoln² poΦet krok∙. Obousm∞rn² iterßtor na to pot°ebuje lineßrnφ Φas (lineßrn∞ ·m∞rn² poΦtu krok∙). To je takΘ jeden z hlavnφch d∙vod∙ zavedenφ tohoto konceptu. Dφky p°φstupu k libovolnΘmu prvku v konstantnφm Φase m∙₧eme velmi efektivn∞ implementovat t°φdφcφ algoritmy.

V tabulce 5 je uvedeno, ₧e iterßtor s nßhodn²m p°φstupem podporuje operaci <. Pokud se ale nad tφm trochu zamyslφte, zjistφte, ₧e jsou podporovßny vÜechny relace: ==, !=, <, >, <=, >=. Rovnost a nerovnost najdeme v konceptu Equality Comparable, kter² je iterßtorem s nßhodn²m p°φstupem zjem≥ovßn. Operace < je zavedena v iterßtoru s nßhodn²m p°φstupem. Ostatnφ operace je mo₧nΘ pomocφ nich realizovat

 

(i > j) prßv∞ tehdy, kdy₧ (!(i < j) && (i != j))á neboli takΘ (j < i)

(i <= j) prßv∞ tehdy, kdy₧ ((i < j) || (i == j))

(i >= j) prßv∞ tehdy, kdy₧ !(i < j)

 

Modelem iterßtoru s nßhodn²m p°φstupem je klasick² ukazatel a stejn∞ tak i iterßtory na STL kontejnerech, t°φdßch vector a deque. Iterßtor na STL kontejneru list sem u₧ nepat°φ. Pokud jde o klasick² ukazatel, asi vßm ji₧ doÜlo, podle Φeho byl vytvo°en koncept iterßtoru s nßhodn²m p°φstupem. Pojem ärychlß iterßtorovß aritmetikaô v tabulce 5 je parafrßzφ rychlΘ adresovΘ aritmetiky klasick²ch ukazatel∙.

Pro zajφmavost: KlasickΘ ukazatele umφ o troÜiΦku vφc ne₧ po₧aduje koncept iterßtoru s nßhodn²m p°φstupem. Jazyk C i C++ toti₧ umo₧≥ujφ napsat:

 

int pole[20];

15[pole] = 3;á // !

 

╪ßdek oznaΦen² vyk°iΦnφkem znamenß totΘ₧ co pole[15] = 3; Jde tedy jen o jinou, alternativnφ syntaxi pro p°φstup k prvk∙m. Osobn∞ jsem se s tφm setkal pouze v uΦebnicφch jazyk∙ C a C++ a manußlech p°ekladaΦ∙, nikdy v reßlnΘm k≤du.

 

operace

zßpis

poznßmky

pohyb vp°ed

i += n

Jestli₧e n > 0 je efekt stejn² jako p°i n‑nßsobnΘm pou₧itφ ++i; jestli₧e n < 0,á je efekt stejn² jako p°i n‑nßsobnΘm pou₧itφ --i; pro n == 0 jde o nulovou operaci. i je nesingulßrnφ, stejn∞ jako n pozic dan²m sm∞rem (podle znamΘnka n).

ärychlß iterßtorovß aritmetikaô

i + n,
n + i

Oba dva zßpisy znamenajφ totΘ₧:
{ TYP tmp = i; return tmp += n; }, kde TYP je typ iterßtoru.

pohyb vzad

i -= n

TotΘ₧ co i += (-n)

ärychlß iterßtorovß aritmetikaô

i û n

TotΘ₧ co i + (-n)

Φtenφ libovolnΘho prvku

i[n]

i + n musφ b²t dereferencovatelnß hodnota, ekvivalentnφ s *(i + n).

zßpis do libovolnΘho prvku

i[n] = a

i + n musφ b²t dereferencovatelnß hodnota, ekvivalentnφ s *(i + n) = a.

rozdφl iterßtor∙

j û i

j musφ b²t dosa₧itelnΘ z i. V²sledkem je hodnota n (typu rozdφlu) takovß, ₧e j == i + n.

porovnßnφ

i < j

j je dosa₧itelnΘ z i, nebo j je dosa₧itelnΘ z i, nebo obojφ. Relace < je ostrΘ slabΘ uspo°ßdßnφ.

 

Tab. 5 Operace iterßtoru s nßhodn²m p°φstupem, vÜechny s konstantnφ Φasovou slo₧itostφ. DalÜφ, zde neuvedenΘ operace jsou shodnΘ s t∞mi od obousm∞rnΘmu iterßtoru.

 

objekt

koncept iterßtoru

klasickΘ pole

Nßhodn² p°φstup

vector

Nßhodn² p°φstup

deque

Nßhodn² p°φstup

string

Nßhodn² p°φstup

list

Nßhodn² p°φstup

set, multiset

Obousm∞rn² iterßtor

map, multimap

Obousm∞rn² iterßtor

vstupnφ datov² proud (istream)

Vstupnφ iterßtor

v²stupnφ datov² proud (ostream)

V²stupnφ iterßtor

 

Tab. 6 JakΘ iterßtory nabφzφ (nejenom) STL kontejnery.

Co nßs jeÜt∞ Φekß

V dalÜφch pokraΦovßnφch nßs Φekajφ modely iterßtor∙ (tj. iterßtory jako typy jazyka C++), podpora knihovny STL pro vytvß°enφ vlastnφch iterßtor∙ a zjiÜ¥ovßnφ vlastnostφ iterßtor∙. VÜimneme si takΘ specialit v podob∞ adaptΘr∙, proxy a iterßtor∙ na vstupn∞/v²stupnφch datov²ch proudech.

Jaroslav Fran∞k

Infotipy
[1] Dokumentace STL od SGI: www.sgi.com\technology\stl
[2] J. Fran∞k, Nebojte se STL, Chip 12/01
[3] J. Fran∞k, Iterßtory I, Chip 01/03
[4] D. Musser et al., STL Tutorial and Reference Guide, 2001
[5] N. Josuttis, The C++ Standard Library, 1999
[6] E. Gamma et al., Design Patterns, 1995
[7] zdrojov² k≤d v rubrice Chip Plus na Chip CD