Iterßtory III. ZnaΦky, rysy, adaptΘry...

Minule jsme si p°edstavili koncepty (metatypy) iterßtor∙. Dnes se budeme bavit p°evß₧n∞ o modelech t∞chto koncept∙, tedy z pohledu C++ o typech a jejich vlastnostech.

ZnaΦkovßnφ iterßtor∙

Iterßtorem m∙₧e b²t klasick² ukazatel a stejn∞ tak i t°φda, kterß implementuje po₧adovanΘ rozhrannφ (s po₧adovanou sΘmantikou). Prost°edky C++ vÜak neumo₧≥ujφ pracovat p°φmo s koncepty; nßzev konceptu lze pou₧φt jako jmΘno ÜablonovΘho parametru a tφm to konΦφ (JeÜt∞ lze s pomocφ jist²ch trik∙ testovat, zda dan² typ je modelem konceptu, ale pouze na syntaktickΘ ·rovni).

Pokud tedy chceme v∞d∞t, zda dan² iterßtor (typ) je vstupnφ, dop°edn² Φi s nßhodn²m p°φstupem musφme si je oznaΦkovat. Ka₧dΘmu iterßtoru p°i°adφme prßv∞ jednu znaΦku, kterß bude oznaΦovat ten nejlepÜφ koncept, jeho₧ je iterßtor modelem. ZnaΦky nebudou nic jinΘho, ne₧ prßzdnΘ C++ t°φdy. Jednomu konceptu odpovφdß jeden datov² typ.

V STL jsou tyto znaΦky definovßny v hlaviΦkovΘm souboru <iterator>. Objektovß hierarchie t∞chto znaΦek odpovφdß p°ibli₧n∞ hierarchii p°φsluÜn²ch koncept∙, viz Obr. 1. Vlastnφ definice t∞chto znaΦek vypadajφ takto (jeden p°φklad za vÜechny)

 

class forward_iterator_tag

áá : public input_iterator_tag

{};

 

 

 

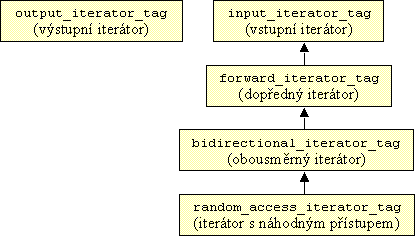
Obr. 1 Objektovß hierarchie znaΦek iterßtor∙.

 

K Φemu je znaΦkovßnφ dobrΘ? StaΦφ si uv∞domit, ₧e n∞kterΘ algoritmy fungujφ efektivn∞ji, kdy₧ majφ k dispozici mocn∞jÜφ iterßtory. Nap°φklad minule zmi≥ovanΘ t°φd∞nφ by fungovalo i s dop°edn²mi iterßtory, ale teprve kdy₧ pou₧ijeme iterßtory s nßhodn²m p°φstupem dostaneme efektivnφ algoritmus. Kdy₧ tohle spojφme s p°et∞₧ovßnφm funkcφ, m∙₧eme dßt t°φdφcφ funkci na v²b∞r mezi obecn∞jÜφm iterßtorem a mßlo efektivnφm algoritmem nebo specializovan²m iterßtorem a efektivnφm algoritmem.

NejlΘpe bude uvΘst si konkrΘtnφ p°φklad. Tentokrßt p∙jde o obrßcenφ po°adφ prvk∙ v posloupnosti (prvnφ bude poslednφ atd.). Zde je mo₧nΘ pou₧φt obousm∞rnΘ iterßtory, ale iterßtory s nßhodn²m p°φstupem dßvajφ efektivn∞jÜφ algoritmus. Nejprve napφÜeme funkci pro obousm∞rnΘ iterßtory a pak pro iterßtory s nßhodn²m p°φstupem:

 

template <typename BidirectionalIterator>

void obrat_poradi(BidirectionalIterator prvni,

ááááá BidirectionalIterator posledni,

ááááá bidirectional_iterator_tag)

{

áá while (true)

áá {

ááááá if ( (prvni == posledni) || (prvni == --posledni) )

áááááááá return;

ááááá else

áááááááá std::iter_swap(prvni++, posledni);

áá }

}

 

template <typename RandomAccessIterator>

void obrat_poradi(RandomAccessIterator prvni,

ááááá RandomAccessIterator posledni,

ááááá random_access_iterator_tag)

{

áá while (prvni < posledni) std::iter_swap(prvni++, --posledni);

 

}

 

Poslednφ t°etφ parametr p°edstavuje znaΦku iterßtoru. Je nepojmenovan², proto₧e jeho instance se v t∞le funkce v∙bec nepou₧ije. Slou₧φ pouze p°ekladaΦi p°i hledßnφ vhodnΘ p°etφ₧enΘ funkce. Na dopln∞nou: STL funkce iter_swap, le₧φcφ v prostoru jmen std, provede prohozenφ hodnot, na n∞₧ odkazujφ jejφ dva parametry û iterßtory.

Po°ßd tomu jeÜt∞ n∞co chybφ û dispeΦer, tedy °φdφcφ funkce, kterß se postarß o zavolßnφ jednΘ z p°edchozφch funkcφ podle toho, jakΘ iterßtory dostane na vstupu. A co chybφ dispeΦerovi? Mo₧nost zeptat se libovolnΘho iterßtoru na jeho znaΦku. Pot°ebujeme tedy t°φdu rys∙ (template traits class), kterß bude implementovat mapovßnφ libovolnΘho typu iterßtoru na p°φsluÜnou znaΦku. STL pro tento ·Φel poskytuje Üablonovou t°φdu rys∙ iterator_traits.

T°φda rys∙ iterßtor∙

èablonovß t°φda rys∙ iterßtor∙, iterator_traits, je definovßna v hlaviΦkovΘm souboru <iterator>. Poskytuje informace nejenom o znaΦce iterßtoru, ale i o typu prvku, typu rozdφlu iterßtor∙, typu ukazatele na prvek a typu reference na prvek. A to vÜechno pro libovoln² iterßtor, kter² je jejφm Üablonov²m argumentem. Definice tΘto t°φdy rys∙ je nßsledujφcφ (jednotlivΘ definice typ∙ jsou uvedeny v po°adφ, v jakΘm byly v²Üe vyjmenovßny)

 

template <typename Iterator>

struct iterator_traits

{

áá typedef typename

ááááá Iterator::iterator_category iterator_category;

áá typedef typename

ááááá Iterator::value_type value_type;

áá typedef typename

ááááá Iterator::difference_type difference_type;

áá typedef typename

ááááá Iterator::pointer pointer;

áá typedef typename

ááááá Iterator::reference reference;

};

 

Struktura ka₧dΘ z on∞ch definicφ typu je nßsledujφcφ: KlφΦovΘ slovo typedef uvßdφ vno°enou definici typu, nßsleduje klφΦovΘ slovo typename, kterΘ p°ekladaΦi napovφ, ₧e nßsledujφcφ v²raz Iterator::iterator_category je oznaΦenφm vno°enΘho typu v typu Iterator. Jako poslednφ se objevφ jmΘno definovanΘho typu, tj. iterator_category.

Tato definice p°edpoklßdß, ₧e iterßtor (typ) je t°φda a mß vno°enΘ definice typ∙. My vÜak z minula vφme, ₧e klasick² ukazatel je rovn∞₧ iterßtor. Co s tφm? Ukazatel p°ece nem∙₧e mφt vno°enΘ definice typ∙. NaÜt∞stφ jsou tu pokroΦilΘ vlastnosti C++, konkrΘtn∞ ΦßsteΦnß specializace Üablony t°φdy. Nic nßm tedy nebrßnφ napsat specializaci pro klasickΘ ukazatele

 

template <typename T>

struct iterator_traits<T *>

{

áá typedef

ááááá random_access_iterator_tag iterator_category;

áá typedef ptrdiff_tá difference_type;

áá typedef Tá value_type;

áá typedef T *á pointer;

áá typedef T & reference;

};

 

template <typename T>

struct iterator_traits<const T *>

{ /* analogicky... */ };

 

Zde jasn∞ °φkßme, ₧e ukazatel je iterßtor s nßhodn²m p°φstupem. Rozdφl dvou ukazatel∙ je v C++ typu ptrdiff_t. Rozhodnutφ, zda pou₧φt nespecializovanou Φi specializovanou Üablonu, je v∞cφ p°ekladaΦe; o to se v∙bec nemusφme starat. Nynφ u₧ m∙₧eme doplnit dv∞ d°φve definovanΘ funkce o jejich dispeΦera

 

template <typename BidirectionalIterator>

void obrat_poradi(BidirectionalIterator prvni,

ááááá BidirectionalIterator posledni)

{

áá obrat_poradi(prvni, posledni,

ááááá iterator_traits<BidirectionalIterator>::iterator_category());

}

 

Nenechte se zmßst, ₧e se vÜechny funkce jmenujφ stejn∞ û o rozliÜenφ se postarß p°ekladaΦ a p°et∞₧ovßnφ funkcφ. Jak znßmo, tam kde funguje koncept, funguje i jeho zjemn∞nφ. Tak₧e tuto funkci m∙₧eme volat takΘ pro iterßtory s nßhodn²m p°φstupem, nebo¥ tento koncept zjem≥uje koncept obousm∞rnΘho iterßtoru (kter² je zde explicitn∞ vy₧adovßn). RozliÜenφ, o jak² koncept iterßtoru se jednß, je uskuteΦn∞no uvnit° funkce, p°i pou₧itφ t°φdy rys∙. Vy₧aduje to vÜak menÜφ vysv∞tlenφ. V²raz

 

iterator_traits<BidirectionalIterator>::iterator_category

 

p°edstavuje typ znaΦky iterßtoru. Nap°φklad

 

iterator_traits<int *>::iterator_category

 

znamenß, jak jist∞ uhodnete, typ random_access_iterator_tag. Ty prßzdnΘ zßvorky za oznaΦenφm typu z toho ud∞lajφ (nepojmenovanou) instanci. Jin²mi slovy: jde o volßnφ implicitnφho konstruktoru.

Zdatn∞jÜφ programßto°i, kte°φ ovlßdajφ ÜablonovΘ metaprogramovßnφ (viz Φlßnek [6]), by to zvlßdli i bez tΘ nepojmenovanΘ instance. Nepou₧ilo by se p°et∞₧ovßnφ funkcφ, ale meta konstrukce, viz ukßzka v [10].

JeÜt∞ jeden zajφmav² p°φklad. Vzpome≥me na v²Üe zmφn∞nou funkci iter_swap. Jejφm ·kolem je prohodit dva prvky, na kterΘ odkazujφ jejφ dva parametry, iterßtory. K prohozenφ prvk∙ pot°ebujeme vytvo°it pomocnou instanci prvku, ale k tomu pot°ebuje znßt typ prvku. Nenφ nic jednoduÜÜφho, ne₧ se zeptat iterßtoru na jeho p°φsluÜn² typ prvku pomocφ t°φdy iterator_traits.

 

template <typename ForwardIterator1,

ááááááááá typename ForwardIterator2>

inline void iter_swap(ForwardIterator1 a,

ááááááá ááForwardIterator2 b)

{

áá iterator_traits<ForwardIterator1>::value_type tmp(*a);

áá *a = *b;

áá *b = tmp;ááá

}

Specifika v²stupnφho iterßtoru

Z minula vφme, ₧e pro v²stupnφ iterßtory nemß smysl definovat typ prvku (value_type) ani typ rozdφlu (difference_type). V STL se to vyjßd°φ tak, ₧e se pou₧ije typ void. Tak₧e t°φda iterator_traits bude mφt pro jak²koliv v²stupnφ iterßtor obsah ekvivalentnφ s

 

{

áá typedef output_iterator_tag iterator_category;

áá typedef void difference_type;

áá typedef void value_type;

áá typedef void pointer;

áá typedef void reference;

};

PφÜeme iterßtor kompatibilnφ s STL

Kdy₧ budeme psßt vlastnφ iterßtor, bude to zcela jist∞ t°φda. Pro kompatibilitu s STL budeme muset zajistit dostupnost rys∙ naÜeho iterßtoru. Zde existuje n∞kolik mo₧nostφ, jak toho dosßhnout.

╪ekn∞me, ₧e jsme vytvo°ili jist² kontejner, t°eba jednosm∞rn² seznam, a zßrove≥ tvo°φme i iterßtor na tomto kontejneru. Je jist∞ jasnΘ, ₧e jednosm∞rn² seznam nem∙₧e nabφdnout vφce ne₧ dop°edn² iterßtor. Zde je kostra definice naÜeho iterßtoru

 

template <typename T> class cJednosmerka

{

áá // ...

};

 

P°edpoklßdejme, ₧e vÜechny vlastnosti, kterΘ vy₧aduje koncept dop°ednΘho iterßtoru, jsou ji₧ sprßvn∞ implementovßny. Nynφ si ukß₧eme, jak z n∞j ud∞lat iterßtor kompatibilnφ s STL, tj. uvedeme do ₧ivota rysy tohoto iterßtoru.

Specializace t°φdy rys∙

Jednou z mo₧nostφ je pou₧itφ ΦßsteΦnΘ specializace Üablony t°φdy rys∙ iterator_traits, tak jako v p°φpad∞ ukazatel∙. Jen₧e zatφmco pro ukazatel to byla jedinß mo₧nost, zde je to spφÜe exces, vy₧adujφcφ navφc ty nejpokroΦilejÜφ vlastnosti (kterΘ bohu₧el n∞kterΘ p°ekladaΦe jeÜt∞ neznajφ) i znalosti C++.

 

template <typename T>

struct iterator_traits<cJednosmerka<T> >

{

áá typedef forward_iterator_tag iterator_category;

áá typedef ptrdiff_t ádifference_type;

áá typedef Tá value_type;

áá typedef T *á pointer;

áá typedef T & reference;

};

RuΦnφ vepsßnφ definic typ∙

DalÜφ mo₧nostφ je äruΦnφ prßceô. Prost∞ do naÜφ t°φdy vepφÜeme pot°ebnΘ definice typ∙. JednoduchΘ a snad i p°ehlednΘ.

 

template <typename T> class cJednosmerka

{

áá // ...

public:

áá typedef forward_iterator_tag iterator_category;

áá typedef ptrdiff_tá difference_type;

áá typedef Tá value_type;

áá typedef T *á pointer;

áá typedef T & reference;

};

Bßzovß t°φda iterator

Pokud si vzpomenete na Φlßnek [5], na to jak jsme z neadaptabilnφch funktor∙ d∞lali adaptabilnφ, vφte, ₧e jsme m∞li v STL k dispozici dv∞ bßzovΘ t°φdy, kterΘ sice samy o sob∞ nebyly funktory, ale poskytovaly pot°ebnΘ definice typ∙. Stejnß situace je i u iterßtor∙. Mßme k dispozici bßzovou t°φdu iterator, kterß sice sama o sob∞ nenφ iterßtorem, ale poskytuje pot°ebnΘ vno°enΘ definice typ∙. Najdeme ji v hlaviΦkovΘm souboru <iterator>. Nßzev je mo₧nß zavßd∞jφcφ, ale s tφm se musφme smφ°it. Definice vypadß takto

 

template <typename Category,

ááááááááá typename T,

ááááááááá typename Distance = ptrdiff_t,

ááááááááá typename Pointer = T*,

ááááááááá typename Reference = T&>

struct iterator

{

áá typedef Category iterator_category;

áá typedef T value_type;

áá typedef Distance difference_type;

áá typedef Pointer pointer;

áá typedef Reference reference;

};

 

S pou₧itφm tΘto t°φdy m∙₧eme aktivovat rysy naÜeho iterßtoru tφm, ₧e ho odvodφme jako potomka

 

template <typename T> class cJednosmerka

áá : public iterator<forward_iterator_tag, T>

{

áá // ...

};

 

VÜimn∞te si, ₧e jsme zadali pouze prvnφ dva ÜablonovΘ argumenty. Ostatnφ majφ svΘ implicitnφ hodnoty, kterΘ ve v∞tÜin∞ p°φpad∙ nenφ nutno m∞nit. Toto je preferovan² zp∙sob.

Specifika v²stupnφho iterßtoru

Jak ji₧ vφme, v²stupnφ iterßtor je pon∞kud zvlßÜtnφ û v∞tÜina jemu asociovan²ch typ∙ je void. Proto mohou mφt vÜechny v²stupnφ iterßtory jednoho p°edka

 

class cJakykolivVystupniIterator

áá : public iterator<output_iterator_tag,

áááááááááááááááááááá void, void, void, void>

{

áá // ...

};

 

Toto zajistφ, ₧e t°φda rys∙ iterator_traits bude obsahovat ty sprßvnΘ ·daje (viz v²Üe).

PomocnΘ funkce

Pro zßkladnφ prßci s iterßtory poskytuje STL dv∞ funkce: advance pro posun iterßtoru o dan² poΦet krok∙ (vp°ed nebo i vzad podle konceptu iterßtoru), distance pro zjiÜt∞nφ vzdßlenosti mezi dv∞ma iterßtory (jeden musφ b²t dosa₧iteln² z druhΘho).

 

template <typename InputIterator, typename Distance>

void advance(InputIterator& i, Distance n);

 

template<typename InputIterator>

typename iterator_traits<InputIterator>::difference_type

distance(InputIterator first, InputIterator last);

 

Tyto funkce jsou implementovßny podobn∞ jako naÜe ädispeΦerskßô funkce v²Üe. To znamenß, ₧e danΘ funkce v₧dy poskytujφ co nejefektivn∞jÜφ algoritmus pro danΘ typy parametr∙. Nap°φklad pro iterßtory s nßhodn²m p°φstupem ob∞ metody pracujφ v konstantnφm Φase, zatφmco pro ostatnφ iterßtory pracujφ v lineßrnφm Φase (·m∞rnΘm poΦtu krok∙). Tak₧e nap°φklad

 

cJednosmerka i;á // + n∞jakß inicializace

cJednosmerka i2;á // + n∞jakß inicializace

advance(i, 10);

int vzdalenost = distance(i, i2);

 

znamenß, ₧e se pro iterßtor i desetkrßt zavolß operßtor ++ a pak se jeÜt∞ provede jist² poΦet iteracφ s kopiφ iterßtoru i, dokud se nedosßhne i2 (jinak toti₧ vzdßlenost urΦit nejde). Kde₧to

 

int j[20];á // + inicializace

int * j2 = j + 20;

advance(j, 10);

int do_konce = distance(j, j2);

 

je ekvivalentnφ operacφm

 

j += 10;

int do_konce = j2 û j;

 

To jen dφky tomu, ₧e ukazatel je iterßtor s nßhodn²m p°φstupem.

PouΦenφ: Nepodce≥ujte tyto funkce. P°i ka₧dΘm p°esunu iterßtoru o v∞tÜφ poΦet krok∙ ne₧ 1 pou₧ijte funkci advance. Pro zjiÜt∞nφ vzdßlenosti mezi dv∞ma (dosa₧iteln²mi) iterßtory v₧dy pou₧ijte funkci distance.

Zp∞tn² iterßtor (adaptΘr)

V∞tÜina STL algoritm∙ pracuje s jist²m rozsahem prvk∙ stylem äod zaΦßtku do konceô, tj. pou₧φvajφ v∞tÜinou operßtor ++ k p°echodu mezi prvky. N∞kdy vÜak m∙₧e b²t ₧ßdoucφ obrßtit sled na äod konce k zaΦßtkuô. Abychom nemuseli p°episovat k≤d algoritm∙, nabφzφ STL adaptΘr iterßtoru, kter² obrßtφ sled prochßzenφ: Jeho operßtor ++ bude vlastn∞ odpovφdat operßtoru --adaptovanΘho iterßtoru a obrßcen∞. Zde je deklarace (hlaviΦkov² soubor <iterator>)

 

template <typename Iterator>

class reverse_iterator

: public iterator

áááááááá <

ááááááááááá typename iterator_traits<Iterator>::iterator_category,

ááááááááááá typename iterator_traits<Iterator>::value_type,

ááááááááááá typename iterator_traits<Iterator>::difference_type,

ááááááááááá typename iterator_traits<Iterator>::pointer,

ááááááááááá typename iterator_traits<Iterator>::reference

áááááááá >

{

áá // ...

áá typedef Iterator iterator_type;

áá explicit reverse_iterator(Iterator x);

áá Iterator base() const;

áá // ...

};

 

Je jasnΘ, ₧e tento adaptΘr nelze pou₧φt na jednosm∞rn² iterßtor. Tak₧e Üablonov²m argumentem m∙₧e b²t obousm∞rn² iterßtor nebo iterßtor s nßhodn²m p°φstupem. Pokud nahlΘdnete do hlaviΦkovΘho souboru s definicφ tohoto adaptΘru, zjistφte, ₧e mß vÜechny metody odpovφdajφcφ konceptu iterßtoru s nßhodn²m p°φstupem; tedy nap°φklad

 

reference operator[](difference_type n) const;

 

pro p°φstup k libovolnΘmu prvku v konstantnφm Φase. Ale co kdy₧ adaptujeme pouze obousm∞rn² iterßtor? Ten p°ece takovou operaci neznß! Je to v po°ßdku? Ano je. Dφky pokroΦil²m vlastnostem C++, konkrΘtn∞ implicitnφmu vytvß°enφ instancφ Üablon: Pokud metodu pou₧iji, vygeneruje se automaticky pot°ebnß instance, ale pokud takovou metodu nepou₧iji, pak jako by nebyla (nevytvo°φ se instance). To znamenß, ₧e bude vÜechno v po°ßdku, dokud se nepokusφm pou₧φt n∞co, co pro obousm∞rnΘ iterßtory nefunguje. Tak₧e pokud adaptujeme obousm∞rnΘ iterßtory, je adaptΘr modelem obousm∞rnΘho iterßtoru. A pokud adaptujeme iterßtor s nßhodn²m p°φstupem je v²sledn² adaptΘr modelem iterßtoru s nßhodn²m p°φstupem.

JeÜt∞ je zde ale menÜφ problΘm s urΦenφm rozsahu pro tento zp∞tn² iterßtor. Dejme tomu, ₧e chceme projφt cel² kontejner. ZaΦφnßme na poslednφm prvku, kter² do rozsahu pat°φ, a tφm pßdem by druh² konec rozsahu m∞l b²t omezen prvnφm neexistujφcφm prvkem p°ed prvnφm prvkem kontejneru. Nic takovΘho vÜak norma nedovoluje (za kontejnerem ano, ale p°ed ne). Proto je pou₧ita finta. Rozsah zaΦφnß na prvnφm prvku za poslednφm a konΦφ na prvnφm prvku, ale zp∞tn² iterßtor odkazuje äo jeden prvekô, viz Φervenß Üipka na Obr. 2. P°esn∞ji by se to nechalo zapsat takto

 

&*(reverse_iterator(i)) == &*(i - 1)

 

Ka₧d² kontejner podporujφcφ obousm∞rnΘ iterßtory poskytuje vno°enΘ definice typ∙ reverse_iterator a const_reverse_iterator, a takΘ metody rbegin() a rend(), kterΘ vracejφ iterßtory t∞chto typ∙, viz Obr. 2.

 

 

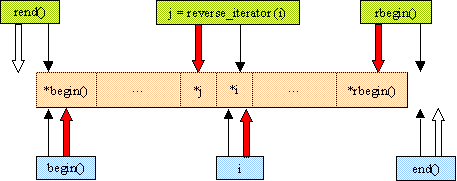
Obr. 2 Zp∞tnΘ iterßtory rend(), rbegin() a j. Plnß Üipka oznaΦuje element, kter² zφskßme pou₧itφm operßtoru dereferencovßnφ, iterßtory rend() a end() nelze dereferencovat.

 

AdaptΘr reverse_iterator obsahuje n∞kolik novinek oproti iterßtor∙m. Tyto jsou vypsßny v deklaraci v ·vodu tΘto sekce. Vno°en² typ iterator_type umo₧≥uje zeptat se na typ adaptovanΘho iterßtoru. Explicitnφ jednoparametrick² konstruktor z iterßtoru ud∞lß zp∞tn² iterßtor, viz j = reverse_iterator(i) na Obr.2. Metoda base() vracφ iterßtor p∙vodnφho, adaptovanΘho typu, kter² odpovφdß aktußlnφ pozici zp∞tnΘho iterßtoru. Toho lze vyu₧φt p°i prßci s kontejnery nap°φklad v nßsledujφcφ situaci: S kontejnerem pracujeme pomocφ zp∞tn²ch iterßtor∙, hledßme t°eba v²skyt jistΘho prvku od konce kontejneru, a pak se rozhodneme tento prvek z kontejneru odstranit. Metoda kontejneru erase vÜak nevezme zp∞tn² iterßtor jako parametr, proto pomocφ metody base() zp∞tnΘho iterßtoru provedeme konverzi a pak u₧ erase bude fungovat.

P°φklady u₧itφ zp∞tn²ch iterßtor∙ najdete v [10]. Zde jen krßtkß ukßzka toho jak vypsat pozpßtku obsah pole na obrazovku v textovΘm re₧imu (ka₧d² prvek na vlastnφ °ßdek)

 

int pole[5] = { 1, 2, 3, 4, 5 };

copy(reverse_iterator<int *>(pole + 5), // rbegin

áááá reverse_iterator<int *>(pole),áááá // rend

áááá ostream_iterator(cout, ô\nô));

 

Mimochodem, vφte jak co nejjednoduÜeji s pou₧itφm STL napsat funkci, kterß zjistφ, zda danΘ slovo (°et∞zec) je palindrom? P°ipome≥me, ₧e palindrom je takovΘ slovo, kterΘ se i pozpßtku Φte stejn∞, nap°. oko, krk, level, atd. Deklarace bude vypadat takto

 

bool je_palindrom(const string & slovo);

 

Zkuste na to p°ijφt (Pro jednoduchost p°edpoklßdejte, ₧e slovo je skuteΦn∞ jedno slovo a neobsahuje mezery.). ╪eÜenφ se dozvφte v p°φÜtφm dφle.

DokonΦenφ p°φÜt∞

Dnes se jeÜt∞ nedostalo na vklßdacφ iterßtory a iterßtory na vstupn∞/v²stupnφch proudech. Budeme se jim v∞novat p°φÜt∞.

Jaroslav Fran∞k

Infotipy
[1] Dokumentace STL od SGI: www.sgi.com\technology\stl
[2] J. Fran∞k, Iteratory I, Chip 01/03
[3] J. Fran∞k, Iteratory II, Chip 01/03
[4] J. Fran∞k, Nebojte se STL, Chip 12/01
[5] J. Fran∞k, Jak se na funktor volß II, Chip 02/02
[6] J. Fran∞k, D°inu nechte p°ekladaΦi!, Chip 01/01
[7] D. Musser et al., STL Tutorial and Reference Guide, 2001
[8] N. Josuttis, The C++ Standard Library, 1999
[9] S. Meyers, Effective STL, 2001
[10] zdrojov² k≤d v rubrice Chip Plus na Chip CD