Iterátory I. Zahřívací kolo
Být „in“ znamená znát a ovládat prostředky, které nabízí standardní knihovna jazyka C++ STL. Děsí vás pojem iterátor? Pak jste tu správně. Připravili jsme pro vás miniseriál, který vás provede standardní knihovnou a seznámí vás s iterátory. Dozvíte se nejenom, co to je iterátor, ale seznámíte se i s prostředky, které STL nabízí, s tím proč tam jsou a jak fungují. Nezapomeneme ani na nejčastější problémy, které někdy dokáží zaskočit i zkušeného programátora.
Proč iterátory
Při programování pracujeme s daty. Pro větší množství souvisejících dat používáme kontejnery, což jsou obecně objekty (nikoli ve smyslu OOP), které umožňují uložit větší množství dat. Uvnitř kontejneru to ale může vypadat různě: Data mohou být uložena za sebou v řadě – pak kontejner nazýváme pole (array znamená řada), příkladem může být klasické céčkovské pole nebo STL třída vector. Data mohou být také pospojována do řady pomocí ukazatelů, pak jde o seznam, příkladem je STL třída list. Nebo pro účely rychlého vyhledávání mohou být data uspořádána do binárního stromu, příkladem jsou třeba STL třídy set a map. Zkrátka uspořádání dat v kontejneru může být všelijaké.
Nyní se zastavíme u algoritmů. Vezměme třeba hledání maximálního prvku v kontejneru (předpokládáme, že to pro naše data má smysl). Úkol, ten zní jasně: projít všechny prvky od prvního do posledního a najít ten největší. Je jisté, že pro tento algoritmus není důležité, jak jsou data uložena, jestli ve stromu nebo v poli – to nemá na maximální prvek vliv. Problém ale je: Co to znamená první prvek? Co znamená poslední prvek? Jak procházet mezi prvky, neboli jak iterovat? Například u pole máme hned jasno, co je první prvek a co poslední, ale co u stromu? A navíc – projít pole prvků znamená také něco úplně jiného než projít všechny větve stromu.
Naštěstí máme iterátory – dávají význam pojmům jako první nebo poslední prvek a umožňují procházet mezi prvky v kontejneru neboli iterovat. Díky iterátorům se algoritmus pro hledání maximálního prvku, ale i mnoho jiných, nemusí zabývat vnitřní skladbou kontejneru. Iterátory odkazují na prvky (jedna instance iterátoru na nejvýše jeden prvek) a navíc implementují logiku procházení mezi prvky v daném kontejneru.
Dříve než přistoupíme k bližšímu popisu, uvědomme si jednu věc: výraz iterátor se používá jak pro obecný koncept (více o konceptech viz [2]), tak pro datový typ a stejně tak i pro instanci. Je to podobné jako u ukazatelů. Když máme např. deklaraci
int * p;
řekneme že int * je ukazatel, a také že p je ukazatel. Z tohoto důvodu v místě, kde bude třeba odlišit význam pojmu iterátor, uvedeme v závorce, zda se jedná o koncept, typ, nebo instanci.
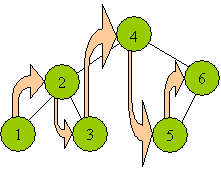
Obr. 1 Takhle bude vypadat iterování ve stromu (STL třída set). Každá šipka odpovídá jedné iteraci.
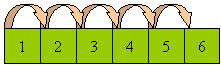
Obr. 2 Iterování v klasickém poli nebo vektoru (STL třída vector). Každá šipka odpovídá jedné iteraci.
Algoritmy a iterátory
Zatím jsme nehovořili o tom, jak takový iterátor vypadá, ale jak vyplyne z následujícího textu, pro používání STL kontejnerů a algoritmů to není nezbytně nutné. Zatím nám bude stačit vědět, že iterátor je taková „černá skříňka“ (black box), označme ji písmenem i, se kterou můžeme, až na několik výjimek, provádět tyto operace:
- dereferencovat: unárním operátorem * získáme přístup k odkazovanému prvku (*i)
- iterovat: pomocí operátoru ++ přejdeme na další prvek v kontejneru (++i, nebo i++)
- porovnávat: pomocí operátorů == a != zjišťujeme, jestli dva iterátory i a j odkazují na stejný prvek (i == j, nebo i != j).
- přiřazovat: pomocí operátoru = zajistíme, že j bude odkazovat na ten samý prvek jako i (přiřazením j = i)
- kopírovat: funguje inicializace kopírováním, tj. j(i).
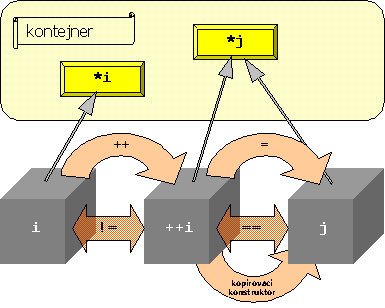
Obr. 3 Iterátor jako černá skříňka.
Nyní si zde ještě připomeneme definici funkce hledající maximální prvek
template <class ITERATOR> // (1)
ITERATOR max_element(ITERATOR prvni, ITERATOR posledni)
// (2)
{
if ( prvni ==
posledni ) return posledni; // (3)
ITERATOR max_prvek
= prvni; // (4)
while ( ++prvni
!= posledni ) // (5)
{
if ( *max_prvek
< *prvni ) max_prvek = first; //
(6)
}
return max_prvek;
// (7)
}
Na vysvětlenou:
(1) Každý kontejner může mít svůj vlastní iterátor (typ), ale algoritmus hledání maximálního prvku zůstane stejný. Proto je typ iterátoru šablonovým parametrem.
(2) Algoritmu zadáme dva iterátory (instance): iterátor na první prvek a iterátor za poslední prvek rozsahu, kterého se týká hledání maxima. Takovéto zadání rozsahu umožňuje hledat maximální prvek třeba jen v určité části kontejneru. Algoritmus vrací iterátor na maximální prvek – nejenže získáme hodnotu maxima (dereferencováním vráceného iterátoru), ale navíc víme, kde maximální prvek v kontejneru leží.
(3) Když jsou si vstupní argumenty rovny, rozsah je prázdný, takže v duchu STL vrátíme iterátor na konec rozsahu (de facto na první prvek za)
(4) Inicializujeme iterování, začínáme od prvního prvku v daném rozsahu.
(5) Podmínka pro ukončení iterace, včetně přechodu na další prvek (++prvni).
(6) Testujeme, jestli prvek určený iterátorem max_prvek je menší, než prvek určený iterátorem prvni. Jak jste si jistě všimli, iterátor prvni je použit k projití zadaného rozsahu a tudíž v těle smyčky vždy znamená začátek dosud nezpracovaného rozsahu (této vlastnosti se říká invariant smyčky, neboť zůstává v platnosti po celou dobu iterování).
(7) Po skončení iterování odkazuje iterátor max_prvek na (první) maximální prvek v daném rozsahu.
To byl příklad typického generického algoritmu. Všimněte si následujících vlastností: Parametrem je jistý rozsah prvků určený (ohraničený) dvěma iterátory. Radši než maximální prvek vrací algoritmus iterátor na maximální prvek. Algoritmus vůbec neví na jakém kontejneru pracuje; pracuje s prvky kontejneru (pomocí iterátorů), nikoli s kontejnerem samotným (proto například nemůže měnit počet prvků kontejneru – později uvidíme, jak je důležité o této vlastnosti vědět).
Kontejnery a iterátory
Nyní nabídneme pohled z druhé strany. Kontejner musí generickému algoritmu poskytnout jistou podporu, aby algoritmus mohl pracovat s jeho prvky. Jde jednak o typové informace (jakého typu je iterátor, konstantní iterátor, prvek kontejneru, atd.) a jednak o poskytnutí iterátorů na první a (za) poslední prvek v kontejneru. Proto každý STL kontejner musí implementovat normou předepsané rozhranní. Nám teď bude stačit vědět, že každý STL kontejner má vnořené definice typů:
iterator typ iterátoru na daném kontejneru
const_iterator typ iterátoru na daném kontejneru s konstantními prvky
value_type typ prvku daného kontejneru
a metody
iterator begin() vrátí iterátor na první prvek
iterator end() vrátí iterátor na první prvek za posledním (norma zaručuje, že to má smysl)
const_iterator begin() const vrátí iterátor na první prvek konstantního kontejneru
const_iterator end() const vrátí iterátor na první prvek za posledním u konstantního kontejneru (norma zaručuje, že to má smysl)
Na příkladu se vše hned objasní. Máme kontejner celých čísel a hledáme maximální prvek.
Nejdříve pro vektor
vector<int> cisla;
// a nějaká inicializace prvků
// kde je maximální prvek?
vector<int>::iterator max_prvek =
max_element(cisla.begin(),
cisla.end());
// kolik to je?
vector<int>::value_type max_hodnota = *max_prvek;
A teď pro seznam
list<int> cisla;
// a nějaká inicializace prvků
// kde je maximální prvek?
list<int>::iterator max_prvek =
max_element(cisla.begin(),
cisla.end());
// kolik to je?
list<int>::value_type max_hodnota = *max_prvek;
Všimněte si, že díky standardizovanému rozhranní obou kontejnerů, se uvedené výpisy téměř neliší. KONTEJNER::iterator je u obou tím správným typem iterátoru pro daný KONTEJNER, begin() vždy znamená začátek a end() vždy konec rozsahu. To proto jsem tvrdil, že není třeba vědět, jak jsou jednotlivé iterátory implementovány, jakého jsou vlastně typu. Díky vnořeným definicím typů (deklarace typedef) se můžeme každého STL kontejneru „zeptat“, jakého typu je jeho iterátor – to je onen výraz KONTEJNER::iterator. Metody begin() a end() vrací iterátory tohoto typu, takže překladač si dokáže vydedukovat správný šablonový argument generické funkce max_element a vygenerovat její příslušnou instanci. Jak vidno, spoustu věcí za nás udělá překladač.
Analogicky to funguje dokonce i pro klasická pole:
int cisla[N] = { /*...*/ };
// kde je maximální prvek?
int * max_prvek = max_element(cisla, cisla + N);
// kolik to je?
int max_hodnota = *max_prvek;
Zde ale nemáme vnořené definice typů ani metody begin() a end(). Uvědomte si ale, že ukazatele jsou také iterátory – podporují všechny operace zmíněné v předešlé sekci, lze jimi zadat hranice klasického pole a implementují přechod mezi prvky v klasickém poli.
Ještě pro úplnost: v případě STL kontejnerů implementovaných pomocí binárního stromu (např. třídy set) lze ve většině případů nahradit použití algoritmu max_element něčím efektivnějším. Tyto kontejnery jsou totiž setříděné.
Důležité pojmy
Abychom si i nadále rozuměli, provedeme upřesnění několika důležitých pojmů, na které při používání iterátorů zcela jistě narazíte.
Rovnost iterátorů
Pokud je pro iterátor (typ) definována rovnost operátorem ==, pak dva iterátory (instance) i a j jsou si rovny, píšeme i == j, pokud odkazují na stejný prvek. Nerovnost iterátorů i != j znamená totéž co !(i == j). Tedy buď oba odkazují na různé prvky, nebo je alespoň jeden z nich singulární (viz dále).
Konstantní a nekonstantní iterátory
Pokud v souvislosti s iterátory mluvíme o konstantnosti a nekonstantnosti, máme vždy na mysli konstantnost a nekonstantnost odkazovaných prvků. Konstantní instance iterátoru totiž postrádá smysl – nešel by aplikovat operátor ++ pro přechod na další prvek.
Konstantní iterátor je tedy iterátor, který umožňuje procházet mezi prvky, ale neumožňuje měnit jejich hodnoty. Nekonstantní iterátor, krátce je iterátor, umožňuje procházet mezi prvky i měnit jejich hodnoty.
Typ prvku
STL kontejner obsahuje prvky jednoho typu, iterátor na tyto prvky odkazuje. Typem prvku u iterátoru rozumíme typ hodnoty, kterou dostaneme, když na iterátor aplikujeme operátor dereferencování *. Například:
vector<int> cisla;
vector<int>::iterator i = cisla.begin();
Typem prvku iterátoru i je typ výrazu *i, tj. v našem případě int.
const vector<int> ccisla; // konstantní kontejner
vector<int>::const_iterator j = ccisla.begin();
Zde je typem prvku iterátoru j typ const int. Vnořený typ const_iterator nám poskytne typ iterátoru pro konstantní instanci třídy vector, a verze metod begin() a end() pro konstantní instance nám vrátí iterátor správného typu.
Anglicky se typ prvku označuje value type. S tímto pojmem se později setkáme u šablonové třídy rysů iterator_traits.
Dosažitelnost
Řekneme, že iterátor j je dosažitelný z iterátoru i, jestliže existuje konečná sekvence aplikací operátoru ++ na iterátor i, která zajistí rovnost i == j. Jinými slovy: z i po konečném počtu iterací přejdeme až do j.
Pokud je iterátor j dosažitelný z iterátoru i, pak oba nutně leží ve stejném kontejneru. Není možné, že bychom se inkrementací iterátoru i dostali „ven“ z kontejneru a po nějakém čase bloudění v paměti „vpadli“ do nějakého jiného kontejneru.
Jestliže jsou i a j různé a j je dosažitelné z i, pak podle naší definice i není dosažitelné z j. Potřebovali bychom zpětný chod, operátor --. Jak uvidíme dále, některé druhy iterátorů toto zvládnou. Mohli bychom tak pro ně definovat reverzibilní dosažitelnost.
Anglický termín pro dosažitelnost je reachability.
Typ rozdílu
Pokud je pro dva iterátory definována rovnost pomocí operátoru == (měly by zároveň být ve stejném kontejneru), je definována i nerovnost operátorem !=. V případě, že se dva nesingulární (viz dále) iterátory i a j nerovnají, může nás zajímat, jak jsou od sebe daleko. Vzdálenost se měří počtem kroků (iterací), které je nutno učinit, abychom se od i dostali k j. Pokud i == j, pak vzdálenost je nulová. Pro i != j musíme rozlišit dva případy: Za prvé, pokud je j dosažitelné z i, tak vzdálenost od i do j je rovna počtu aplikací operátoru ++ nutných na dosažení j z i. Za druhé zbývá už jen možnost, kdy i je dosažitelné z j, pak vzdálenost od i do j je rovna záporně vzatému počtu aplikací operátoru ++ nutných na dosažení i z j. Typ rozdílu tedy musí být celé číslo se znaménkem.
Anglicky se typ rozdílu označuje difference type a setkáme se s ním u šablonové třídy rysů iterator_traits.
Prvek za koncem kontejneru
Určitě víte, že když deklarujeme klasické pole N prvků, máme k dispozici i adresu prvku N+1 (jelikož indexování začíná vždy nulou, má tento index N). Pro osvěžení paměti
const int N = 20;
int pole[N]
= { /*...*/ };
for (
int * i = pole; i < &pole[N]; ++i ) { /*...*/ }
// nebo
for (
int * i = pole; i < pole + N; ++i ) { /*...*/ }
Zvýrazněné části jsou adresy neexistujícího prvku za koncem pole. Norma jazyka C++ (ale i C) zajišťuje, že tato adresa má vždy smysl.
Analogie uvedeného pravidla platí i pro všechny iterátory. Implementace knihovny STL musí zajistit, aby iterátor na první „neexistující prvek“ za koncem kontejneru měl smysl. S takovými iterátory se setkáváme častěji, než by se zdálo. Například iterátor, který vrátí metoda end() je iterátorem na neexistující prvek za posledním prvkem v příslušném kontejneru.
Anglicky tyto prvky nazýváme past-the-end values, nebo také one past-the-end.
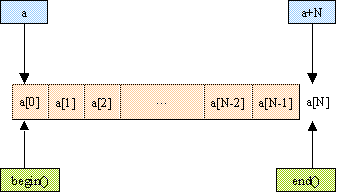
Obr. 4 Neexistující prvek za koncem kontejneru.
Dereferencovatelné hodnoty iterátorů
Iterátor (typ) sice implementuje operátor dereferencování *, ale ne všechny jejich instance jdou dereferencovat. Například už zmiňované iterátory na prvky za koncem kontejneru nejdou dereferencovat. To znamená, že nejde napsat (s využitím předchozího příkladu)
int pole[N] = { /* ... */ };
int a = pole[N]; // !!! NELZE
pole[N]
= 0; // !!! NELZE
Adresa tohoto prvku sice existuje, ale prvek samotný nikoliv. Stejně tak nelze dereferencovat iterátor získaný metodou end()
vector<int>
cisla; // a nějaká inicializace prvků
int a
= *cisla.end(); // !!! NELZE
*cisla.end() = 0; // !!! NELZE
Takže dereferencovatelné hodnoty iterátorů jsou takové instance iterátorů, kde použití operátoru * k získání odkazovaného prvku má smysl.
Singulární hodnoty iterátorů
Stejně jako neinicializované ukazatele (ukazatele ukazující nikam), můžeme mít i neinicializované iterátory. Takové iterátory neodkazují na žádný prvek v žádném kontejneru. Jediné, co lze s takovým iterátorem dělat, je přiřadit mu nějakou nesingulární hodnotu, tj. nechat ho odkazovat na nějaký prvek v nějakém kontejneru.
Je jistě zřejmé, že dereferencovatelné hodnoty iterátorů a iterátory odkazující na první prvek za koncem kontejneru jsou nesingulární.
Rozsah
Dostáváme se ke snad nejdůležitějšímu pojmu, tím je rozsah. Pokud máme dva nesingulární iterátory i a j na stejném kontejneru a j je dosažitelné z i (budeme uvažovat pouze platné rozsahy), pak můžeme definovat rozsah takto: Je to množina všech iterátorů i počínaje, které dostaneme z i aplikováním operátoru ++ tak dlouho dokud nedosáhneme j, přičemž j do rozsahu nezahrneme. Lidově řečeno: všechno mezi i a j, včetně i a mimo j. Rozsah iterátorů můžeme označit stejně jako interval čísel v matematice
[i, j)
Tento zápis znamená, že i do daného rozsahu patří (V českých krajích se používá spíše lomená závorka, ale většina počítačové literatury je v angličtině, proto si dovolím napsat to takto.) a j tam nepatří.
Proč tam j nepatří? Je k tomu nějaký rozumný důvod? Ano je, například celkem snadno můžeme označit prázdný rozsah takto
[i, i)
Když si místo iterátorů představíme celá čísla, kolik prvků má množina [m,n)? Přesně m-n. Kdybychom se na totéž zeptali u množiny [m,n], vyšlo by nám m-n+1 a to už není tak hezké.
Celý rozsah libovolného STL kontejneru, pojmenovaného např. cisla, lze vyjádřit takto
[cisla.begin(),
cisla.end() )
Už víme, že metoda end() vrací iterátor na první prvek za posledním, který do zpracovávaného rozsahu nepatří.

Obr. 5 Rozsah [i,j). Barevně podloženy jsou odpovídající prvky.
Ohlédnutí do minulosti i současnosti
Iterátory nejsou výsadou STL. Je to obecný programovací vzor (design pattern, viz [6]), který se používal ještě před tím, než přišla STL. Pamětníci možná zaznamenali přítomnost iterátorů v knihovně datových typů BIDS (Borland International Data Structures), která se distribuovala s oblíbeným překladačem Borland C++ 3.1.
Moderní programovací jazyky jako Java a C# také umožňují práci s iterátory.
Iterátor a další programovací vzory
V souvislosti s iterátory se (v STL) používají ještě další programovací vzory: adaptér a proxy, podrobně popsané v [6]. O adaptérech jsme si už povídali v souvislosti s funktory [3]. Adaptér přizpůsobí rozhranní adaptovaného objektu jiným potřebám. Například adaptér reverse_iterator, jak jméno napovídá, změní směr procházení prvků od konce k začátku.
Proxy je tzv. zástupný objekt. Představte si, že máte hodně velký kontejner, který se nevejde celý do operační paměti. Je tedy z větší části uložen na pevném disku. I na takovém kontejneru lze požít iterátory – budou však vracet proxy a nikoli odkazované objekty. Proxy se postará, v případě přístupu k danému prvku, o načtení prvku z disku do paměti.
Dalším příkladem proxy jsou tzv. vkládací iterátory. To jsou iterátory, které umožňují vkládat do kontejneru nové prvky. V úvodu tohoto článku jsem zdůraznil, že iterátory nemohou měnit počet prvků v kontejneru – to je pravda, ale v kombinaci s proxy to jde. Jak? – To se dozvíte v jednom z následujících dílů.
Příště
Po úvodním seznámení se základními pojmy nahlédneme příště do STL a představíme si koncepty iterátorů, které tato knihovna používá.
Jaroslav Franěk
 Infotipy
Infotipy
[1] Dokumentace
STL od SGI: www.sgi.com\technology\stl
[2] J. Franěk, Nebojte se STL, Chip 12/01
[3] J. Franěk, Jak se na funktor volá I., Chip 01/02
[4] D. Musser et al., STL Tutorial and Reference Guide, 2001
[5] N. Josuttis, The C++ Standard Library, 1999
[6] E. Gamma et al., Design Patterns, 1995
[7] zdrojový kód v rubrice Chip Plus na Chip CD