C/C++ & Visual C++
Kurz DirectX (34.)
┌vodem | DatovΘ struktury | Kurz DirectX | Downloads | Otßzky a odpov∞di | 2001 | 2002 | 2003 | 2004
V tΘto lekci dßle upravφme pohyb kamery, kter² jsme naΦali v minulΘ lekci. Doplnφme formßt souboru cesty a pou₧ijeme jin² typ interpolace mezi segmenty. Dßle si n∞co povφme o technice Level Of Detail (LOD). V tΘto lekci si povφme, jak LOD obecn∞ funguje a p°φÜt∞ zkusφme implementovat jednoduch² LOD do naÜeho enginu.
34.1. Pohyb kamery - pokraΦovßnφ
P°edstavte si, ₧e chceme rotovat kolem n∞jakΘho objektu. Zde bychom m∞li velk² problΘm p°i definici sm∞rov²ch vektor∙. V tomto p°φpad∞ by se nßramn∞ hodilo, abychom sm∞r kamery definovali pomocφ druhΘho bodu. Definujeme tedy look-at point a eye point. V n∞kter²ch p°φpadech se ovÜem hodφ ob∞ varianty, proto zavedeme specißlnφ znaΦenφ °ßdk∙, kterΘ pou₧φvajφ prvnφ nebo druhou mo₧nost:
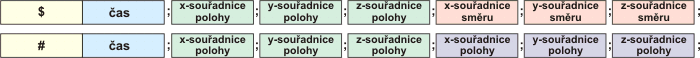
Pokud na zaΦßtek °ßdku napφÜeme znak dolar ($), poslednφ parametr se interpretuje jako sm∞rov² vektor. Pokud mφsto dolaru pou₧ijeme k°φ₧ek (#), parametr se interpretuje jako bod s tφm, ₧e pokud pou₧ijete star² formßt, pou₧ije se prvnφ varianta.
Zm∞ny k≤du jsou minimßlnφ, v metod∞ LoadPath() p°ibude testovßnφ prvnφho znaku na °ßdku:
// Second vector is look at point
if(pline[0] == '#')
{
bLookAtPoint = TRUE;
// Jump over '#'
pline++;
}
if(pline[0] == '$')
{
// Jump over '$'
pline++;
}
V tomto p°φpad∞ se tento znak p°eskoΦφ a zßrove≥ nastavφme p°φsluÜn² flag, na kter² reagujeme po naΦtenφ ostatnφch hodnot na °ßdku:
// vDir is look at point
if(bLookAtPoint)
{
ps.vDir = ps.vDir - ps.vPos;
bLookAtPoint = FALSE;
}
Touto operacφ spoΦφtßme sm∞rov² vektor, kter² bychom jinak museli vklßdat p°φmo do souboru cesty. V p°φpad∞ k°φ₧ku se tento znak pouze p°eskoΦφ. Na zßv∞r tΘto metody jeÜt∞ provedeme zacyklenφ spojovΘho seznamu. To se nßm bude hodit v zßp∞tφ, a₧ budeme implementovat novou interpolaΦnφ metodu:
// Cycle path - last next is first and first previous is last
pLast->pNext = m_arPath;
m_arPath->pPrevious = pLast;
Nßslednφka poslednφho segmentu nastavφme na prvnφ a p°edchßzejφcφ prvnφho nastavφme jako poslednφ. Dejte si ovÜem pozor, a₧ budete spojov² seznam odstra≥ovat z pam∞ti, kde se sleduje prßv∞ hodnota NULL poslednφho prvku - nynφ ₧ßdnß NULL hodnota nikde nenφ.
Catmull-rom interpolace
Jednß se o specißlnφ interpolaci, kterß pro v²poΦet vyu₧φvß hned 4 bod∙ na k°ivce (u lineßrnφ staΦily pouze dva). K°ivka mezi t∞mito body p°ipomφnß Bezierovu k°ivku, rozdφl je v tom, ₧e v p°φpad∞ Catmull-rom k°ivka prochßzφ p°es °φdφcφ body. Nebudu se tu v∞novat konkrΘtnφm vzorc∙m, jak spoΦφtat interpolovan² vektor. Na internetu se dß najφt mnoho podrobn²ch Φlßnk∙ k tΘto problematice.
Direct3D podporuje tuto interpolaci v podob∞ funkce D3DXVec3CatmullRom(), kterß vlastn∞ ud∞lß vÜechno za vßs. Mß Üest parametr∙: ukazatel na v²stupnφ vektor, Φty°i ukazatele na vektory, z kter²ch se v²sledn² vektor poΦφtß a faktor interpolace - podobn∞ jako u lineßrnφ interpolace. Pro urΦenφ v²stupnφho vektoru je krom∞ bod∙ ohraniΦujφcφ aktußlnφ segment pot°eba dalÜφ dva body - jsou to sousedi hraniΦnφch bod∙. Z toho plyne, ₧e nejde urΦit sprßvn∞ vektor v prvnφm a poslednφm segmentu pokud nenφ k°ivka cyklickß. Proto jsme tedy nßÜ spojov² seznam zacyklili. Na nßsledujφcφm obrßzku je vid∞t, co jsem te∩ popsal:
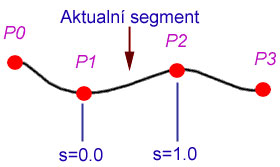
Body P0-P3 jsou pot°eba pro v²poΦet interpolace v aktußlnφm segmentu. Parametr s je nßÜ interpolaΦnφ faktor, kter² poΦφtßme v metod∞ ProcessCamera().
D∙le₧it²m momentem je tedy v²b∞r sprßvn²ch bod∙, z nich₧ se poΦφtß interpolace:
ps1 = ps2 = ps3 = ps4 = m_curSeg;
if(m_curSeg->pPrevious)
{
ps1 = m_curSeg->pPrevious;
}
if(m_curSeg->pNext)
{
ps3 = m_curSeg->pNext;
}
if(m_curSeg->pNext->pNext)
{
ps4 = m_curSeg->pNext->pNext;
}
Testovat hodnoty bychom ani nemuseli, proto₧e v celΘm spojovΘm seznamu by se nem∞la vyskytovat hodnota NULL. PotΘ ji₧ m∙₧eme zavolat funkci D3DXVec3CatmullRom() pro oba vektory:
D3DXVec3CatmullRom(&m_curInterpolation.vPos, &ps1->vPos, &ps2->vPos, &ps3->vPos, &ps4->vPos, s);
D3DXVec3CatmullRom(&m_curInterpolation.vDir, &ps1->vDir, &ps2->vDir, &ps3->vDir, &ps4->vDir, s);
Zachoval jsem i lineßrnφ interpolaci pro srovnßnφ. Velkß v²hoda tΘto novΘ interpolace toti₧ spoΦφvß v tom, ₧e pohyb je mnohem plynulejÜφ a nedochßzφ k ostr²m zm∞nßm sm∞ru.
34.2. Level of Detail (LOD)
Tato technika vyu₧φvß toho, ₧e vzdßlenΘ Φßsti terΘnu nemusφ b²t vykresleny ve vysok²ch detailech jako Φßsti nejblφ₧e k pozorovateli. My te∩ vykreslujeme vÜe stejn∞ detailn∞ a u vzdßlen²ch list∙ ani jednotlivΘ detaily nerozeznßme. Tento problΘm °eÜφ prßv∞ LOD, kde krom∞ jinΘho dosßhneme v²raznΘho nav²Üenφ v²konu.
╚φm je list dßle od kamery, tφm vφc vynechßme troj·helnφk∙ a malΘ troj·helnφky spojujeme do v∞tÜφch a v∞tÜφch. Nejvzdßlen∞jÜφ listy nahradφme pouze dv∞ma troj·helnφky!
Jak u₧ to b²vß, i zde se najdou problΘmy, kterΘ se obtφ₧n∞ °eÜφ. P°edstavte se dva navazujφcφ listy, kterΘ jsou velmi ΦlenitΘ v mφst∞ p°echodu (pokud mluvφm o Φlenitosti, mßm na mysli velkΘ rozdφly nadmo°skΘ v²Üky na malΘm prostoru). Algoritmus nahradφ druh² list mΘn∞ detailnφm listem a druh² list ponechß. Nynφ nastane ne₧ßdoucφ efekt, kdy mezi prvnφm a druh²m listem vznikne mezera, bu∩ dφra "za" terΘn nebo p°evis. Toto chovßnφ m∙₧e b²t znaΦn∞ nep°φjemnΘ a terΘn ve v²sledku nevypadß moc p∞kn∞. ╪eÜenφ je mnoho. My si zde ukß₧eme jedno z t∞ch jednoduÜÜφch, kterΘ nenφ dokonalΘ. Pro ka₧d² list spoΦφtßme p°i inicializaci faktor p°ev²Üenφ listu. Pokud je tato hodnota p°φliÜ vysokß, znamenß to, ₧e tento list je velmi Φlenit² a tudφ₧ ho budeme nahrazovat se zpo₧d∞nφm - Φili a₧ bude opravdu daleko. Tak₧e nahrazovßnφ nebude zßvislΘ pouze na vzdßlenosti od kamery, ale takΘ na reliΘfu listu. DalÜφm vylepÜenφm by t°eba mohl b²t zp∙sob, kdy navφc porovnßme faktory okolnφch list∙ apod. Mo₧nostφ je hodn∞. ProblΘm s dφrami jsme vy°eÜili, ale zßrove≥ jsme trochu zhorÜili ·Φinnost celΘ techniky. Ale i p°esto je redukce kreslen²ch troj·helnφk∙ v²raznß a nßr∙st FPS rovn∞₧.
Jak budeme techniku implementovat v naÜem terΘnu? Ka₧d² list obsahuje seznam sv²ch index∙ VèECH troj·helnφk∙. Zde mßme na v²b∞r. Bu∩ vyu₧ijeme tento seznam pro vÜechny ·rovn∞ LODu a budeme vybφrat ty sprßvnΘ troj·helnφky, co₧ se projevφ mφrnou Φasovou ztrßtou p°i o°ezßvßnφ list∙ nebo vytvo°φme dalÜφ seznamy nov²ch index∙, kterΘ obsahujφ v₧dy indexy pro jednu ·rove≥. Druhß mo₧nost zase zabere vφce pam∞¥ovΘho mφsta, ale bude trochu rychlejÜφ. Zkusit si m∙₧ete ob∞ varianty, jß zde ukß₧i pouze druhou zmφn∞nou. Upravφme tedy strukturu QTNode tak, ₧e p°idßme novΘ pole index∙ celkem pro 5 ·rovnφ (mßme listy 16x16, to bude 1. ·rove≥, dßle budeme vytvß°et listy 8x8, 4x4, 2x2 a 1x1 pro 5. ·rove≥). P°idejme tedy tyto atributy:
//
// Indexy pro list a pocet indexu
// LOD urovne 1
WORD *pIndices1;
WORD wInd1Count;
WORD wTiles1Count;
// LOD urovne 2
WORD *pIndices2;
WORD wInd2Count;
WORD wTiles2Count;
// LOD urovne 3
WORD *pIndices3;
WORD wInd3Count;
WORD wTiles3Count;
// LOD urovne 4
WORD *pIndices4;
WORD wInd4Count;
WORD wTiles4Count;
// LOD urovne 5
WORD *pIndices5;
WORD wInd5Count;
WORD wTiles5Count;
// Faktor pro pozdejsi uplatneni urovne LOD
// Je to rozdil maximalni a minimalni vysky vertexu v danem listu
float fLODFac;
pIndicesX je pole index∙ X-tΘ ·rovn∞, wIndXCount je poΦet index∙ X-tΘ ·rovn∞ a wTilesXCount je poΦet polφΦek na X-tΘ ·rovni (to bude 16x16, 8x8, 4x4, 2x2 nebo 1x1). Atribut fLODFac je ji₧ zmφn∞n² faktor zvln∞nφ listu. PoΦty index∙ a polφΦek bychom samoz°ejm∞ mohli poΦφtat a₧ v dob∞ o°ezßvßnφ, ale jsou to konstanty, tak proΦ je nemφt p°ipravenΘ (vÜimn∞te si, ₧e op∞t na ·kor pam∞ti, ale tak to je tΘm∞° v₧dy).
Nejd∙le₧it∞jÜφ nynφ bude inicializace vÜech seznam∙. Nejprve alokujeme pam∞¥ pro tyto seznamy:
// allocate space for indices
pNode->wInd1Count = LEAF_I_SIZE*LEAF_I_SIZE*2*3;
pNode->pIndices1 = new WORD[pNode->wInd1Count];
pNode->wTiles1Count = LEAF_I_SIZE*LEAF_I_SIZE;
// allocate space for indices
pNode->wInd2Count = LEAF_I_SIZE/2*LEAF_I_SIZE/2*2*3;
pNode->pIndices2 = new WORD[pNode->wInd2Count];
pNode->wTiles2Count = LEAF_I_SIZE/2*LEAF_I_SIZE/2;
// allocate space for indices
pNode->wInd3Count = LEAF_I_SIZE/4*LEAF_I_SIZE/4*2*3;
pNode->pIndices3 = new WORD[pNode->wInd3Count];
pNode->wTiles3Count = LEAF_I_SIZE/4*LEAF_I_SIZE/4;
// allocate space for indices
pNode->wInd4Count = LEAF_I_SIZE/8*LEAF_I_SIZE/8*2*3;
pNode->pIndices4 = new WORD[pNode->wInd4Count];
pNode->wTiles4Count = LEAF_I_SIZE/8*LEAF_I_SIZE/8;
// allocate space for indices
pNode->wInd5Count = LEAF_I_SIZE/16*LEAF_I_SIZE/16*2*3;
pNode->pIndices5 = new WORD[pNode->wInd5Count];
pNode->wTiles5Count = LEAF_I_SIZE/16*LEAF_I_SIZE/16;
Ka₧dß dalÜφ ·rove≥ mß 1/4 index∙ co p°edchozφ, proto₧e obsahuje 4x mΘn∞ polφΦek. Nynφ nßsleduje smyΦka p°es cel² list, ve kterΘ najednou naplnφme vÜechny seznamy:
for(y = pNode->arBounds[0].y; y < pNode->arBounds[3].y; y++)
{
for(x = pNode->arBounds[0].x; x < pNode->arBounds[3].x; x++)
{
if(m_arTerrain[x][y].vecPos.z > MaxZ)
{
MaxZ = m_arTerrain[x][y].vecPos.z;
}
if(m_arTerrain[x][y].vecPos.z < MinZ)
{
MinZ = m_arTerrain[x][y].vecPos.z;
}
bx = x % LOC_SIZE;
by = y % LOC_SIZE;
pNode->pIndices1[i + 0] = bx + by * LOC_V_SIZE;
pNode->pIndices1[i + 1] = (bx+1) + by * LOC_V_SIZE;
pNode->pIndices1[i + 2] = bx + (by+1) * LOC_V_SIZE;
if(x % 2 == 0 && y % 2 == 0)
{
pNode->pIndices2[i2 + 0] = bx + by * LOC_V_SIZE;
pNode->pIndices2[i2 + 1] = (bx+2) + by * LOC_V_SIZE;
pNode->pIndices2[i2 + 2] = bx + (by+2) * LOC_V_SIZE;
i2 += 3;
}
if(x % 4 == 0 && y % 4 == 0)
{
pNode->pIndices3[i3 + 0] = bx + by * LOC_V_SIZE;
pNode->pIndices3[i3 + 1] = (bx+4) + by * LOC_V_SIZE;
pNode->pIndices3[i3 + 2] = bx + (by+4) * LOC_V_SIZE;
i3 += 3;
}
if(x % 8 == 0 && y % 8 == 0)
{
pNode->pIndices4[i4 + 0] = bx + by * LOC_V_SIZE;
pNode->pIndices4[i4 + 1] = (bx+8) + by * LOC_V_SIZE;
pNode->pIndices4[i4 + 2] = bx + (by+8) * LOC_V_SIZE;
i4 += 3;
}
if(x % 16 == 0 && y % 16 == 0)
{
pNode->pIndices5[i5 + 0] = bx + by * LOC_V_SIZE;
pNode->pIndices5[i5 + 1] = (bx+16) + by * LOC_V_SIZE;
pNode->pIndices5[i5 + 2] = bx + (by+16) * LOC_V_SIZE;
i5 += 3;
}
i += 3;
pNode->pIndices1[i + 0] = (bx+1) + by * LOC_V_SIZE;
pNode->pIndices1[i + 1] = (bx+1) + (by+1) * LOC_V_SIZE;
pNode->pIndices1[i + 2] = bx + (by+1) * LOC_V_SIZE;
if(x % 2 == 0 && y % 2 == 0)
{
pNode->pIndices2[i2 + 0] = (bx+2) + by * LOC_V_SIZE;
pNode->pIndices2[i2 + 1] = (bx+2) + (by+2) * LOC_V_SIZE;
pNode->pIndices2[i2 + 2] = bx + (by+2) * LOC_V_SIZE;
i2 += 3;
}
if(x % 4 == 0 && y % 4 == 0)
{
pNode->pIndices3[i3 + 0] = (bx+4) + by * LOC_V_SIZE;
pNode->pIndices3[i3 + 1] = (bx+4) + (by+4) * LOC_V_SIZE;
pNode->pIndices3[i3 + 2] = bx + (by+4) * LOC_V_SIZE;
i3 += 3;
}
if(x % 8 == 0 && y % 8 == 0)
{
pNode->pIndices4[i4 + 0] = (bx+8) + by * LOC_V_SIZE;
pNode->pIndices4[i4 + 1] = (bx+8) + (by+8) * LOC_V_SIZE;
pNode->pIndices4[i4 + 2] = bx + (by+8) * LOC_V_SIZE;
i4 += 3;
}
if(x % 16 == 0 && y % 16 == 0)
{
pNode->pIndices5[i5 + 0] = (bx+16) + by * LOC_V_SIZE;
pNode->pIndices5[i5 + 1] = (bx+16) + (by+16) * LOC_V_SIZE;
pNode->pIndices5[i5 + 2] = bx + (by+16) * LOC_V_SIZE;
i5 += 3;
}
i += 3;
}
}
V ka₧dΘm opakovßnφ inicializujeme hned 6 index∙ pro celΘ polφΦko (dva troj·helnφky). Pro p°ehlednost jsem barevn∞ odd∞lil jednotlivΘ ·rovn∞. Zßkladnφ 1. ·rove≥ je zelenß a nikterak se neliÜφ od p°edeÜl²ch dφl∙. Jen si vÜimn∞te, ₧e ka₧d² cyklus se do seznamu zapφÜe 6 index∙. Zajφmav∞jÜφ bude Φervenß neboli 2. ·rove≥. Zde se zapisuje jen ka₧d² vertex, Φili skßΦe se ob jeden vertex a tφm se vytvo°φ sφ¥ s poloviΦnφ hustotou. Takto pokraΦujeme p°es modrou, fialovou a nakonec ₧lutou ·rove≥ kdy z listu ud∞lßme jedno velkΘ pole (zapφÜe vlastn∞ jen 6 index∙ pro dva troj·helnφky). TakΘ si vÜimn∞te, ₧e ka₧dß ·rove≥ mß svΘ poΦφtadlo iX pro index na X-tΘ ·rovni.
V prvnφ Φßsti cyklu vybφrßme maximßlnφ a minimßlnφ v²Üku vertexu. Tyto hodnoty v zßp∞tφ pou₧ijeme na v²poΦet faktoru:
pNode->fLODFac = MaxZ - MinZ;
Naposledy upravφme metodu CullTerrain(), kde vybereme sprßvnou ·rove≥ a zkopφrujeme p°φsluÜnΘ indexy. V p°φpad∞, ₧e je LOD aktivnφ, spoΦφtßme vzdßlenost od kamery a list "p°iblφ₧φme" o faktor. Slo₧it∞jÜφ listy se tak budou zdßt blφ₧e a nenahradφ se, i kdy₧ ve skuteΦnosti jsou daleko:
// Vzdalenost listu od kamery - pocita se pouze pro LOD urovne > 1
if(m_iLODLevel != 0)
{
CreateDisplayObject(DISIID_IDisplay, (void**) &pDis);
v1 = D3DXVECTOR3((float)pNode->arBounds[3].x, (float)pNode->arBounds[3].y, pNode->arBounds[3].z);
v2 = *pDis->GetCamera()->GetEyePoint();
d = D3DXVec3Length(&(v1 - v2));
// Faktorem list umele priblizime, pokud je faktor vysoky
// znamena to, ze list je hodne clenity a tudiz nelze
// nahradit jednodussim provedenim a proto ho umele priblizime
// a tim zpusobime, ze se nenahradi
d -= pNode->fLODFac * (MAX_LOD_LEVEL-m_iLODLevel);
SAFE_RELEASE(pDis);
}
Dßle budeme vybφrat ·rovn∞ podle vzdßlenosti:
if(d < 150.0f)
{
int lw = pNode->pLocation->m_iVisTiles * 6;
// Zkopirovani vsech indexu listu do spravne pozice IB
memcpy(pNode->pLocation->pIndices+lw, pNode->pIndices1, pNode->wInd1Count*sizeof(WORD));
// Zvysit pocet viditelnych listu pro danou lokaci
// Opet se vyuzije pri renderingu (pocita se pocet primitiv)
pNode->pLocation->m_iVisQuads++;
pNode->pLocation->m_iVisTiles += pNode->wTiles1Count;
}
else
{
if(d >= 150.0f && d < 200.f)
{
int lw = pNode->pLocation->m_iVisTiles * 6;
// Zkopirovani vsech indexu listu do spravne pozice IB
memcpy(pNode->pLocation->pIndices+lw, pNode->pIndices2, pNode->wInd2Count*sizeof(WORD));
// Zvysit pocet viditelnych listu pro danou lokaci
// Opet se vyuzije pri renderingu (pocita se pocet primitiv)
pNode->pLocation->m_iVisQuads++;
pNode->pLocation->m_iVisTiles += pNode->wTiles2Count;
}
else
...
}
K≤d zde neuvßdφm cel², proto₧e podmφnky se stßle opakujφ a₧ na ·rove≥ 5. V₧dy ovÜem musφme kopφrovat indexy ze sprßvnΘ ·rovn∞ a nakonec zv²Üit poΦet polφΦek v rßmci lokace - ka₧dß ·rove≥ mß tento poΦet jin²! A to je vÜe! Nynφ se bude mφsto 400 000 polygon∙ vykreslovat pouze okolo 40 000 polygon∙.
Cel² p°φklad si samoz°ejm∞ m∙₧ete stßhnout v sekci Downloads.
34.3. Zßv∞r
Na zßv∞r uvedu obrßzek ze souΦasnΘ verze naÜeho 3D enginu s technikou LOD:
Je vid∞t, ₧e vzdßlenΘ kopce u₧ jsou mßlo detailnφ a jevφ se jen jako mraky v dßlce... V programu m∙₧ete m∞nit interpolaΦnφ metodu klßvesou I. Pokud zapnete lineßrnφ interpolaci, je vid∞t, ₧e pohyb je vφce sekan² ne₧ v p°φpad∞ Catmull-rom interpolace.
V p°φÜtφ lekci se vrßtφm k normßlov²m vektor∙m a ukß₧eme si jednoduch² zp∙sob, jak je spoΦφtat p°esn∞! Krom toho si tyto vektory zobrazφme nad terΘnem.
T∞Üφm se p°φÜt∞ nashledanou.