C/C++ & Visual C++
DatovΘ struktury a algoritmy (14.)
┌vodem | DatovΘ struktury | Kurz DirectX | Downloads | Otßzky a odpov∞di | 2001 | 2002 | 2003 | 2004
Minule jsme si ukßzali metody, kter²mi lze navÜtφvit ka₧d² uzel stromu, byly to metody preorder, inorder a takΘ postorder. VÜechny tyto metody prochßzely strom do hloubky. V dneÜnφm pokraΦovßnφ se podφvßme na pr∙chod stromem do Üφ°ky. Teorie je velice p∞knß v∞c, ale lepÜφ jsou praktickΘ ukßzky vyu₧itφ pr∙chodu stromem a tak se i my podφvßme na dva p°φklady. Jeden bude dnes a na ten druh² se podφvßme p°φÜt∞.
14.1. Pr∙chod stromem do Üφ°ky
Op∞t se jednß o ·lohu, kdy je naÜφm cφlem navÜtφvit vÜechny uzly stromu. U metod, se kter²mi jsme se seznßmili minule, jsme postupovali do hloubky, vyÜli jsme z ko°enu a prochßzeli jsme nap°φklad jeho lev²m podstromem, a₧ jsme se dostali k list∙m stromu. U pr∙chodu do Üφ°ky prochßzφme jednotlivΘ hladiny stromu. Jako prvnφ tedy navÜtφvφme op∞t ko°en, potΘ se podφvßme na vÜechny jeho nßsledovnφky a pokraΦujeme a₧ op∞t a₧ k list∙m. Navφc volφme sm∞r zleva doprava.
U prochßzenφ do hloubky, tedy jejφ nerekurzivnφ verze, jsme vyu₧ili datovΘ struktury zßsobnφku. Pro realizaci pr∙chodu do Üφ°ky vyu₧ijeme frontu, kterou op∞t p°epφÜeme do dynamickΘ reprezentace, abychom mohli prochßzet libovoln∞ rozsßhlΘ stromy. Nejprve vlo₧φme do fronty uzel a p°i ka₧dΘm pr∙chodu z fronty jeden uzel vyjmeme a zpracujeme ho. PotΘ vlo₧φme do fronty nßsledovnφky, pokud n∞jakΘ mß. Jestli₧e je nßsledovnφku vφce, pak je vlo₧φme v po°adφ zleva doprava. FunkΦnost, jak jsme si ji popsali v²Üe, pak zajistφ ji₧ fronta. Nejprve si ukß₧eme implementaci fronty:
#ifndef CDYNFRONTA_H
#define CDYNFRONTA_H
template<class T> class CPrvek {
private:
T m_Data;
CPrvek<T> *m_lpDalsi;
public:
CPrvek() : m_lpDalsi(NULL) { }
CPrvek(const T& _Data) : m_Data(_Data), m_lpDalsi(NULL) { }
T VratData() const { return m_Data; }
CPrvek<T>* VratDalsi() const { return m_lpDalsi; }
void NastavDalsi(CPrvek<T> *_lpDalsi) { m_lpDalsi = _lpDalsi; }
void NastavData(const T& _Data) { m_Data = _Data; }
};
template<class T> class CDynFronta {
private:
CPrvek<T> *m_lpVrchol, *m_lpPosledni;
public:
CDynFronta() : m_lpVrchol(NULL), m_lpPosledni(NULL) { }
~CDynFronta() { if(!JePrazdna()) { SmazFrontu(); } }
void VytvorPrazdnou();
bool SmazFrontu();
bool JePrazdna() { return (m_lpVrchol == NULL); }
bool Vloz(const T& _Data); // vklada na konec seznamu
bool Vyjmi(T &_Vyber); // odebere prvni prvek
};
template<class T> void CDynFronta<T>::VytvorPrazdnou()
{
if(m_lpVrchol)
{
SmazFrontu();
}
m_lpVrchol = NULL;
m_lpPosledni = NULL;
}
template<class T> bool CDynFronta<T>::SmazFrontu()
{
bool bNavrat = false;
if(!JePrazdna())
{
CPrvek<T> *lpMazany;
while(m_lpVrchol)
{
lpMazany = m_lpVrchol;
m_lpVrchol = m_lpVrchol->VratDalsi(); // posun na dalsi prvek
delete lpMazany;
}
bNavrat = true;
}
return bNavrat;
}
template<class T> bool CDynFronta<T>::Vloz(const T& _Data)
{
bool bNavrat = false;
// jen vlozime prvek do fronty
CPrvek<T> *lpNovy = new CPrvek<T>(_Data);
if(lpNovy)
{
if(m_lpVrchol == NULL) // je to tedy prvni prvek
{
m_lpVrchol = lpNovy;
m_lpPosledni = lpNovy; // zacatek i konec jsou si rovny
}
else
{
m_lpPosledni->NastavDalsi(lpNovy);
m_lpPosledni = lpNovy; // zapojime na konec fronty
}
bNavrat = true;
}
// opet novy prvek nemazeme
return bNavrat;
}
template<class T> bool CDynFronta<T>::Vyjmi(T &_Vyber)
{
bool bNavrat = false;
if(!JePrazdna())
{
_Vyber = m_lpVrchol->VratData();
CPrvek<T> *lpMazany = m_lpVrchol;
m_lpVrchol = m_lpVrchol->VratDalsi(); // odebereme prvni prvek
delete lpMazany;
bNavrat = true;
}
return bNavrat;
}
#endif
Pou₧φvßme ukazatel na konec i zaΦßtek fronty pro urychlenφ prßce. Pokud bychom m∞li ukazatel jen na zaΦßtek, bylo by p°i ka₧dΘm vklßdßnφ nutnΘ projφt frontou prvk∙ od zaΦßtku a nelΘzt poslednφ prvek.
Nynφ si ukß₧eme metodu vykonßvajφcφ pr∙chod stromem do Üφ°ky:
template<class T> void CBinStrom<T>::PruchodStromem5()
{
typedef CUzel<T> LPTCUZEL;
CDynFronta<LPTCUZEL> Fronta;
if(!JePrazdny()) // overime, jestli ve stromu neco je
{
Fronta.Vloz(*m_lpKoren);
}
CUzel<T> Zpracovani;
while(!Fronta.JePrazdna())
{
if(Fronta.Vyjmi(Zpracovani))
{
cout << Zpracovani.VratData() << " ";
// ukladame zleva doprava
if(Zpracovani.VratLevy()) { Fronta.Vloz(*Zpracovani.VratLevy()); }
if(Zpracovani.VratPravy()) { Fronta.Vloz(*Zpracovani.VratPravy()); }
// mohly by nasledovat dalsi prvky u obecnych stromu
}
}
}
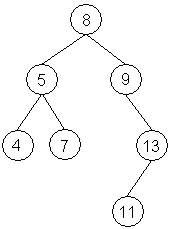
P°idal jsem podmφnku pro ov∞°enφ, zda-li je strom prßzdn², jinak bychom uklßdali do fronty nesmyslnou hodnotu a doÜlo by k vyvolßnφ v²jimky. V minulΘm dφlu tato podmφnka chyb∞la u nerekurzivnφho pr∙chodu stromem do hloubky. P°ipomeneme si, jak nßÜ strom vypadß a ukß₧eme si v²stup programu po zavolßnφ metody PruchodStromem5():
V²stup programu bude: 8, 5, 9, 4, 7, 13, 11.
K≤d naleznete v sekci Downloads (projekt Strom).
14.2. Vyu₧itφ prohledßvßnφ do hloubky a do Üφ°ky
Ukß₧eme si dva p°φklßdky na vyu₧itφ pr∙chodu stromem, jeden bude vyu₧φvat pr∙chod do hloubky a druh² do Üφ°ky. Pokud budeme programovat nap°φklad n∞jakou hru, pak se budeme na poΦßtku nachßzet v n∞jakΘm stavu. R∙zn²mi p°echody do dalÜφch stav∙ se budeme sna₧it dojφt a₧ k °eÜenφ ·lohy. ╪eÜenφ ·lohy m∙₧e b²t jednoznaΦnΘ nebo m∙₧e b²t vφce stav∙, kterΘ jsou °eÜenφm, ·loha je pak mnohoznaΦnß. Zßkladnφmi ·lohami, kterΘ se uvßd∞jφ u pr∙chod∙ jsou logickΘ ·lohy na Üachovnici. Po ka₧dΘm provedenΘm tahu se nßm nask²tß vφce mo₧nostφ na dalÜφ tah, p°iΦem₧ nikdy nevφme, a samoz°ejm∞ to nelze ani p°edem spoΦφtat, jestli nßmi vybran² tah povede ke sprßvnΘmu °eÜenφ.
Jako prvnφ ·lohu budeme °eÜit problΘm, jak kon∞m umφst∞n²m na libovolnΘm mφst∞ Üachovnice proskßkat vÜechna pole, navφc budeme chtφt, aby ka₧dΘ pole bylo navÜtφveno pouze jednou. Jako druhou ·lohu si zvolφme nalezenφ nejkratÜφ cesty kon∞m mezi dv∞ma libovoln²mi mφsty na Üachovnici.
Nejprve si tedy povφme pravidla Üachu. K∙≥ se pohybuje do tvaru pφsmene L, pohyb lze tedy vykonat o jedno pole v jednom sm∞ru a potΘ o dv∞ pole ve sm∞ru na n∞j kolmΘm. Dßma ohro₧uje pole, kterß le₧φ vlevo, vpravo, naho°e a dole od nφ a navφc jeÜt∞ pole na diagonßlßch.
Vrhn∞me se nynφ na navr₧enφ datov²ch struktur pro pohyby kon∞m. Pohyby kon∞, je jich celkem osm, ulo₧φme do pole struktur. Tyto struktury budou obsahovat prßv∞ sou°adnice mo₧n²ch skok∙ kon∞m. Vzhledem k tomu, ₧e strom vÜech mo₧n²ch tah∙ kon∞m by byl velice rozsßhl², budeme vytvß°et pr∙b∞₧n∞ s ka₧d²m tahem. Tedy v pam∞ti poΦφtaΦe se nikdy nebude vyskytovat kompletnφ strom.
Nynφ si rozebereme p°φklady podrobn∞ji a zvlßÜ¥ a to v po°adφ v jakΘm jsme si ukßzali algoritmy pr∙chodu.
14.2.1. Prohledßvßnφ do hloubky
┌loha o projitφ celΘho hracφho pole kon∞m vede na pr∙chod stromem do hloubky. Vrcholy stromu majφ v²znam jednotliv²ch situacφ na hernφm poli. Jako ko°en mßme stav, kdy k∙≥ stojφ na urΦitΘm mφst∞. V ka₧dΘm nßsledujφcφm tahu mßme podle pozice kon∞ a₧ osm mo₧nostφ, jak lze kon∞m tßhnout. MenÜφ poΦet mo₧nostφ bude jednak u mφst kterß jsou blφzko kraj∙m Üachovnice, ale s postupn²m prochßzenφm Üachovnice i u vnit°nφch polφ, abychom vyhov∞li podmφnce o pouze jednΘ nßvÜt∞v∞ polφΦka (a hned s prvnφm pohybem bude maximßlnφ poΦtu mo₧n²ch tah∙ jen 7). Situace, kdy k∙≥ nem∙₧e pokraΦovat, a¥ u₧ proto, ₧e dosßhl °eÜenφ ·lohy nebo nem∙₧e splnit pravidla pro pohyb v dalÜφm kroku, jsou reprezentovßna listy pomyslnΘho stromu.
Tak₧e nejprve si vytvo°φme strukturu pro tahy kon∞m a definujeme n∞kterΘ konstanty:
#define SirkaPole 8
#define VyskaPole 8
#define MaxPocetTahu ((SirkaPole * VyskaPole) - 1)
typedef struct {
int dx; // zmena v x
int dy; // zmena v y
} TahKonem;
// osm moznych tahu konem
TahKonem MozneTahy[8] = { {2,1}, {1,2}, {-1,2}, {-2,1}, {-2,-1}, {-1,-2}, {1,-2}, {2,-1} };
Na po°adφ tah∙ v poli mo₧n²ch tah∙ nezßle₧φ, nebo¥ °eÜenφ nalezneme ve vÜech p°φpadech. OvÜem n∞kterΘ kombinace mohou trvat velmi dlouho, proto₧e v nep°φzniv²ch p°φpadech budeme muset projφt velkou Φßst pomyslnΘho stromu.
Tahy kon∞m budeme provßd∞t na Üachovnici, definovanΘ jako pole cel²ch Φφsel. Dßle napφÜeme metody pro tisk hracφho pole a pro jeho inicializaci. Hodnota -1 bude znamenat, ₧e pole jeÜt∞ nebylo kon∞m navÜtφveno. Ostatnφ Φφsla znamenajφ, v kterΘm tahu k∙≥ danΘ pole navÜtφvil a Φφslovat zaΦφnßme od 0:
int Sachovnice[SirkaPole][VyskaPole];
void TiskSachovnice()
{
for(int i = 0; i < SirkaPole; i++)
{
for(int j = 0; j < VyskaPole; j++)
{
cout << setw(4) << Sachovnice[i][j];
}
cout << endl << endl;
}
}
void VymazSachovnici()
{
for(int i = 0; i < SirkaPole; i++)
{
for(int j = 0; j < VyskaPole; j++)
{
Sachovnice[i][j] = -1;
}
}
}
Nynφ u₧ k vlastnφ funkci, kterß bude provßd∞t jednotlivΘ tahy. Jejφmi parametry budou Φφslo tahu, pozice kon∞ a odkazem p°edßvanß prom∞nnß, kterß signalizuje, zda je cesta nalezena, nebo ne:
void UdelejTah(int _iCislo, int _PozX, int _PozY, bool *_bTahOK)
{
int iTah = 0;
bool bTahOK = false;
int NoveX, NoveY;
do
{
NoveX = _PozX + MozneTahy[iTah].dx;
NoveY = _PozY + MozneTahy[iTah].dy;
iTah++; // priste zkusime dalsi tah
if((NoveX >= 0) && (NoveX < SirkaPole) && (NoveY >= 0) && (NoveY < VyskaPole))
{
// jsme stale na sachovnici
if(Sachovnice[NoveX][NoveY] == -1)
{
// jeste jsme na tomto poli nebyli
Sachovnice[NoveX][NoveY] = _iCislo;
if(_iCislo < MaxPocetTahu) // pokud tah nebyl posledni, zkus dalsi
{
// zkusime dalsi tah
UdelejTah(_iCislo + 1, NoveX, NoveY, &bTahOK);
if(!bTahOK)
{
// pokud tah neni mozny, pak ho zrusime - nastavime na -1
Sachovnice[NoveX][NoveY] = -1;
}
}
else
{
bTahOK = true;
}
}
}
} while (!bTahOK && (iTah < 8));
*_bTahOK = bTahOK; // vratime hodnotu pres parametr
}
Funkce jednoduÜe provßdφ tahy podle po°adφ v poli mo₧n²ch tah∙. K p∙vodnφ pozici kon∞, kterß je p°edßna jako parametr p°iΦte pohyb kon∞. Pokud toto pole le₧φ uvnit° Üachovnice, tak tento tah provede. PoslΘze ov∞°φ, zda nebylo dosud provedeno Üφ°ka * v²Üka zmenÜenß o 1 tah∙, co₧ by znamenalo, ₧e celß Üachovnice je obsazena. Pokud ne, zkusφ ud∞lat dalÜφ tah. P°es parametr se vrßtφ hodnota true nebo false podle toho, zda tato posloupnost tah∙ vede k °eÜenφ. Jestli tomu tak nenφ, pak jednoduÜe tah vrßtφme nastavenφm polφΦka na -1 a p°ejdeme k dalÜφmu pr∙chodu cyklem - zkusφme z pole mo₧n²ch tah∙ nßsledujφcφ tah.
Funkce main() pak vypadß nßsledovn∞:
int main(int argc, char* argv[])
{
int PozX, PozY;
cout << "Zadej x souradnici kone: ";
cin >> PozX;
cout << "Zadej y souradnici kone: ";
cin >> PozY;
if((PozX >= 0) && (PozX < SirkaPole) && (PozY >= 0) && (PozY < VyskaPole))
{
VymazSachovnici();
Sachovnice[PozX][PozY] = 0; // prvni pole
bool bOK;
UdelejTah(1, PozX, PozY, &bOK);
// pokud ma bOK hodnotu true, mame zaplnenou sachovnici tahy konem - staci ji vytisknout
if(bOK)
{
TiskSachovnice();
}
else
{
cout << "Cesta konem nebyla nalezena" << endl;
}
}
else
{
cout << endl << "Zadana pozice lezi mimo hraci pole" << endl;
}
char c;
cin >> c;
return 0;
}
Zeptßme se u₧ivatele na pozici kon∞, velikost Üachovnice se dß m∞nit jen pomocφ konstant a tedy i nßslednΘ rekompilace. Nebyl by vÜak problΘm zm∞nit statickou alokaci na dynamickou. Ov∞°φme, zda pozice kon∞ le₧φ uvnit° Üachovnice. Pokud ano, pak nastavφme prvnφ pole jako v²chozφ (dßme na n∞j 0). PotΘ u₧ jen zavolßme v²Üe popsanou rekurzivnφ metodu.
K≤d naleznete v sekci Downloads (projekt PruchodKonem1).
14.3. Co bude p°φÜt∞
Jak jsme si slφbili v ·vodu, v p°φÜtφm dφlu se podφvßme na pr∙chod stromem do Üφ°ky v podob∞ p°φkladu. Mo₧nß si jeÜt∞ ukß₧eme jednu velice znßmou ·lohu na pr∙chod stromem do Üφ°ky. A pak budeme porovnßvat oba algoritmy z hlediska pou₧itelnosti. T∞Üφm se nashledanou u dalÜφho dφlu.