Best-fit line

We call  best-fit line to the line that passes most closely through several coordinates, minimising the distances between the line and the actual points.

The aim now is to identify the function whose curve is the line.

Note: Bersoft Image Measurements only supports lineal functions (straight lines).

Suppose you have some data involving two variables, in the form of several pairs of values for them. To find about the relationship between the variables, the first step is to plot the pairs of values as coordinates of points on a graph, using the tool.

Then, click   on the Measurement window toolbar, so the program calculates the best-fit straight line and draws it as a new measurement segment on your graph. The line will pass through or close to as many of the points as possible.

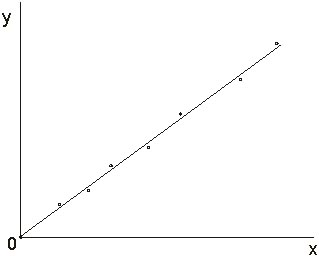
Notice that the best-fit line does not necessarily pass through any of the points plotted.

The calculation results will be appended as comments to the segment drawn to show the best-fit line, and after the calculation is done, an small window showing the measurement comments will be shown.

It is advisable to set the origin of coordinates to the lower-left point in the Preferences window, before using the best-fit line feature, in order to get the proper values.

Results example (as shown in the comments window).:

Lower-left origin
y = a + x * b
a = 559.499399218985
b = -2.05181736257134
y = 559.499399218985 + x * - 2.05181736257134
r = -0.97296016350337

Two-variable Statistics and Linear Regression

Two  variable statistics make possible the development of a relationship (correlation) between two sets of data. Each pair of data has x and y values. From these sets of data a line of regression can be established. The relationship of the two sets of data by use of the straight line method is called Linear Regression. In Linear Regression there are three important values, r, a, and b.

The equation of the straight line is y  = a + bx, where a is the point at which the line crosses the Y-axis and b is the slope of the line.

The correlation coefficient r shows the relationship between two sets of data. A perfect correlation between two values is an r equal to 1 (-1 is a perfect negative correlation); in other words, by knowing the value of one variable you can predict with 100% accuracy the value of the other variable. The further the value of r is from 1, the less reliable will your predictions be. The following table can be used as a set of definitions of the values of the correlation coefficient: