Zatmění Slunce je astronomický úkaz, který nastane tehdy, je-li Slunce na naší obloze zakryto Měsícem.
V této době je Měsíc v novu, ze Země tedy můžeme vidět Měsíc z jeho neosvětlené strany.
Při každém novu však zatmění Slunce nenastává. Je to způsobeno tím, že
rovina, ve které obíhá Měsíc kolem Země, není totožná s rovinou ekliptiky, tj. rovinou, ve které obíhá naše
Země kolem Slunce. Úhel těchto dvou rovin se s časem periodicky mění. Jeho střední hodnota je 5° 43' 43.4"
a mění se s periodou 173 dní a amplitudou asi 9'. Sluneční zatmění může tedy nastat jen tehdy, je-li Měsíc
v novu dostatečně blízko ekliptiky. Tato skutečnost dokonce dala vzniknout samotnému názvu ekliptika.
Ekleiptikos znamená v řečtině zatmění.
Typy slunečních zatmění
Slunce je asi 400× dále od Země než Měsíc, je však asi 400× větší. Tato shoda způsobila, že
Slunce a Měsíc mají na pozemské obloze přibližně stejný úhlový průměr. Vzhledem k tomu, že ani
zemská dráha kolem Slunce, ani dráha Měsíce kolem Země nejsou kružnice, ale elipsy, mění se
vzdálenosti jak Země od Slunce, tak Měsíce od Země. Může pak nastat případ, že Měsíc má
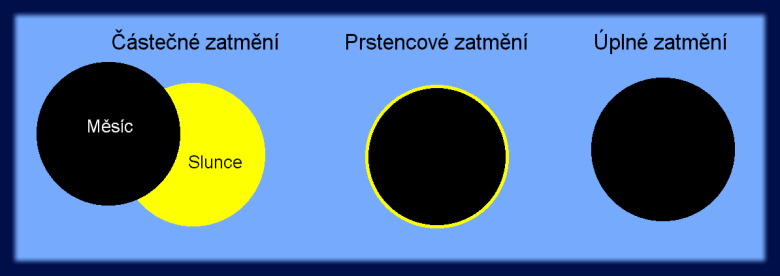
větší úhlové rozměry než Slunce, i případ opačný. Zatmění Slunce proto může být úplné, částečné
nebo prstencové. Pokud úhlový průměr Slunce i Měsíce je téměř dokonale stejný, může nastat i tzv.
hybridní zatmění, při kterém se prstenconé zatmění změní v úplné nebo naopak, jak měsíční
stín běží po zemském povrchu.
Centrální a necentrální zatmění
Centrální zatmění Slunce nastává tehdy, když přímka určená středem Slunce a Měsíce protne Zemi.
Při takovém zatmění nastane v určité oblasti na Zemi úplné nebo prstencové zatmění.
Pokud nastane zatmění, při kterém uvedená přímka Zemi neprotne, nazývá se zatmění necentrální. Při
necentrálních zatměních může úplné nebo prstencové zatmění nastat jen zcela výjimečně a na velmi malém
území.
Pás totality
Oblast na zemském povrchu, kde je v daný okamžik úplné zatmění Slunce, má přibližně tvar elipsy.
Tato elipsa se pohybuje rychlostí poněkud menší než 1 km/s po zemském povrchu a postupně vykreslí
tzv. pás totality. Šířka tohoto pásu, kde je vidět úplné zatmění, může být maximálně 270 km
(při zatmění 11.8.1999 jen 112.1 km). Pás totality má po obou stranách podstatně širší pásy,
ve kterých je vidět zatmění částečné.
Trvání úplného zatmění Slunce
Úplné zatmění Slunce je bohužel velmi krátký úkaz. Nejdelší možné úplné zatmění může trvat
7 minut 31 sekund (zatmění 11. 8. 1999 trvalo však maximálně 2 min 22.9 sec, a to v Rumunsku). Vzhledem
k tomu, že jedno úplné zatmění připadá na 1 až 2 roky a na jednom konkrétním místě na zeměkouli se
opakují úplná zatmění v průměru asi po 360 letech, je úplné zatmění Slunce skutečně velmi vzácné.
Perioda Saros
Zatmění Slunce (podobně i
zatmění Měsíce) se periodicky opakují.
Toto bylo známo již i některým
starověkým civilizacím. Klíčem k pochopení této periodicity je objevení cyklu Saros (název Saros
poprvé použil Edmund Halley a toto slovo přejal z jazyka starých Babylóňanů - saros znamená klíč).
Délka jednoho cyklu (perioda) Saros je S = 6585 dnů 7 hodin 42 minut. Přepočteno na
roky je to 18 let a 10.3 dne nebo 11.3 dne (záleží na počtu přestupných let). Perioda Saros se dá odvodit
ze znalosti následujících tří period:
Synodický měsíc M = 29.53059 dní = 29d 12h 44min
Drakonický měsíc D = 27.21222 dní = 27d 05h 06min
Anomalistický měsíc A = 27.55455 dní = 27d 13h 19min
Synodický měsíc je doba mezi dvěma novy. Drakonický měsíc je doba mezi dvěma průchody Měsíce uzlem -
průsečíkem ekliptiky a dráhy Měsíce na obloze. Anomalistický měsíc je doba mezi dvěma průchody Měsíce perigeem -
bodem na dráze Měsíce, kde je nejblíže Zemi. Saros je nejkratší perioda, kdy současně proběhne celistvý
počet period
M,
D,
A.
S = 223 M S = 242 D S = 239 A (*)
Uvedené rovnosti jsou splněny pouze přibližně, s chybou několika hodin. Znamená to, že libovolná dvě
zatmění Slunce (totéž platí i pro zatmění Měsíce), která jsou v čase oddělena periodou Saros, nastanou
za velmi podobných geometrických podmínek. Nastanou však na různých místech Země, neboť perioda Saros
není rovna celému počtu dní, ale 6 585 a asi 1/3 dne. Za tuto 1/3 dne se Země otočí asi o 120°, takže
následující zatmění po uplynutí periody Saros je posunuto v zeměpisné délce asi o 120° na západ.
Teprve po uplynutí 3 period Saros se tedy zatmění vrátí přibližně na místo se stejnou zeměpisnou
délkou na Zemi. Toto místo však nemá stejnou zeměpisnou šířku, což je způsobeno tím, že rovnosti
(*)
neplatí zcela přesně a Měsíc po uplynutí periody Saros změní poněkud svou vzdálenost od uzlu, tedy i od
ekliptiky. Tato chyba též způsobuje, že zatmění, která se opakují s periodou Saros, se neopakují stále.
Po určité době tato chyba způsobí, že se periody
M,
D a
A natolik rozfázují, že zatmění již nenastane.
Cyklus Saros
Jak bylo vysvětleno v předešlém odstavci, zatmění opakující se s periodou Saros nemohou existovat věčně,
ale jen asi 12 až 13 století. Tím vznikají "rodiny" zatmění patřících k sobě, nazývající se cykly Saros.
Jednotlivá zatmění jedné rodiny jsou v čase oddělena
periodou Saros. Cykly Saros se číslují a jsou velmi užitečné pro pochopení
toho, kdy a kde se vyskytne zatmění Slunce či Měsíce. Bez pochopení tohoto cyklu se výskyt zatmění
může jevit jako chaotický.
Dva typy cyklu Saros
Ekliptika a dráha Měsíce na naší obloze tvoří dvě kružnice, které se protínají ve dvou bodech - uzlech.
Jeden z těchto bodů se nazývá výstupný uzel (Měsíc v něm vystupuje při svém pohybu nad ekliptiku při
pohledu ze severní polokoule), druhý se nazývá sestupný uzel. Měsíc se při pohybu po zemské obloze
opožďuje oproti hvězdám. Znamená to, že každý další den vychází o necelou hodinu později než den předešlý.
Posouvá se tedy po své dráze na obloze vzhledem k hvězdám i uzlům směrem od západu na východ.
Zatmění Slunce nastane, když v novu Měsíc
není od některého z uzlů vzdálen více než asi 18°. Po uplynutí periody Saros se Měsíc nevrátí
zcela přesně na stejné místo vzhledem k uzlu, ale nepatrně se posune.
Při přesném výpočtu totiž zjistíme, že není přesně
223 M = 242 D, ale
223 M > 242 D.
Měsíc se tedy po uplynutí periody Saros zpozdí na své dráze a v novu se posune vzhledem k uzlu směrem
na západ. Zpoždění činí
223 M - 242 D = 0.03567 dne.
Za tuto dobu se Měsíc posune asi o 0.5° vzhledem k uzlu. Závěrem lze tedy říci, že Měsíc
zůstane v pásmu kolem uzlu, kde nastávají zatmění Slunce, po dobu 70 až 80 period Saros.
Za tuto dobu proběhne tedy 70 až 80 zatmění Slunce, z nichž je asi 50 centrálních, ostatní jsou
necentrální. Průběh cyklu Saros, je-li Měsíc poblíž výstupného uzlu, je jiný, než když je Měsíc
poblíž sestupného uzlu.
Průběh cyklu Saros, je-li Měsíc poblíž sestupného uzlu
První zatmění cyklu nastane, když je Měsíc asi 18° východně od sestupného uzlu (tj. nachází se
"pod" ekliptikou). Měsíční stín mine Zemi asi ve vzdálenosti 3 500 km, a to "pod" jižním pólem.
Zemi zasáhne jen polostín. V okolí jižního pólu nastane (malé) částečné zatmění. Při druhém zatmění
cyklu (po uplunutí periody Saros) se stín posune asi o 300 km blíže Zemi a nastane poněkud větší
částečné zatmění, opět viditelné jen na jižní polokouli. Po 10 až 11 periodách (asi 200 let) Saros
nastane první centrální zatmění a u jižního pólu je viditelné poprvé úplné nebo prstencové zatmění.
Po následujících asi 950 let nastávají stále centrální zatmění, přičemž pás totality se posouvá
stále více na sever. Uprostřed tohoto období vznikají nejdelší zatmění kolem rovníku. Poslední
centrální zatmění nastane v okolí severního pólu. Pak následuje 10 až 11 částečných zatmění, která
skončí malým částečným zatměním v okolí severního pólu. Tím celý cyklus Saros skončí asi po 13
stoletích.
Průběh cyklu Saros, je-li Měsíc poblíž výstupného uzlu
První zatmění cyklu nastane, když je Měsíc asi 18° východně od výstupného uzlu (tj. nachází se
"nad" ekliptikou). Měsíční stín mine Zemi asi ve vzdálenosti 3 500 km, tentokrát však "nad" severním pólem.
V okolí severního pólu nastane první (částečné) zatmění.
Při každém dalším zatmění cyklu se stín posune asi o 300 km blíže Zemi, až nastane první cetrální
zatmění v okolí severního pólu. Pak se zatmění posouvají stále k jihu a cyklus skončí v okolí jižního
pólu. Oproti výše popsanému průběhu jde vše v opačném sledu.
Počet současně probíhajících cyklů Saros
V jednom roce nastává na zeměkouli 2 - 5 slunečních zatmění. Každé zatmění musí patřit do některého
cyklu Saros. Vzhledem k tomu, že každému cyklu Saros odpovídá jedno zatmění Slunce asi jednou za 18 let,
vyjde nám, že současně musí probíhat asi kolem čtyřiceti
různých cyklů Saros. Průběžně staré cykly zanikají a nové vznikají. Např. ve druhé polovině 20. století
probíhala zatmění celkem 41 cyklů, z nichž 26 cyklů bylo ve stádiu, kdy vznikají centrální zatmění.
Právě to, že probíhá více cyklů současně, může vytvářet mylný dojem, že zatmění se objevují
chaoticky. Zatmění 11.8.1999 bylo 21. z 77 zatmění cyklu
Saros 145.
