double value that is closer than any other
to 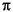 , the ratio of the circumference of a circle to its diameter.
, the ratio of the circumference of a circle to its diameter.
Oh, back to the days that were free from care in the 'Ology 'varsity shop,
With nothing to do but analyse air in an anemometrical top,
Or the differentiation of the trigonometrical pow'rs
Of the constant pi that made me sigh in those happy days of ours!
—I. W. Litchfield, Take Me Back to Tech (1885)
The class Math contains useful basic numerical constants and methods.
public final classMath{ public static final doubleE= 2.7182818284590452354; public static final doublePI= 3.14159265358979323846; public static doublesin(double a); public static doublecos(double a); public static doubletan(double a); public static doubleasin(double a); public static doubleacos(double a); public static doubleatan(double a); public static doubleatan2(double a, double b); public static doubleexp(double a); public static doublelog(double a); public static doublesqrt(double a); public static doublepow(double a, double b); public static doubleIEEEremainder(double f1, double f2); public static doubleceil(double a); public static doublefloor(double a); public static doublerint(double a); public static intround(float a); public static longround(double a); public static doublerandom(); public static intabs(int a); public static longabs(long a); public static floatabs(float a); public static doubleabs(double a); public static intmin(int a, int b); public static longmin(long a, long b); public static floatmin(float a, float b); public static doublemin(double a, double b); public static intmax(int a, int b); public static longmax(long a, long b); public static floatmax(float a, float b); public static doublemax(double a, double b); }
To ensure portability of Java programs, the specifications of many of the numerical functions in this package require that they produce the same results as certain published algorithms. These algorithms are available from the well-known network library netlib as the package fdlibm ("Freely Distributable Math Library"). These algorithms, which are written in the C programming language, are to be understood as if executed in Java execution order with all floating-point operations following the rules of Java floating-point arithmetic.
The network library may be found at
http://netlib.att.com/ on
the World Wide Web; then perform a keyword search for fdlibm. The library may also be retrieved by E-mail; to begin the process, send a message containing the line:
send index from fdlibm
to netlib@research.att.com. The Java math library is defined with respect to
the version of fdlibm dated 95/01/04. Where fdlibm provides more than one definition for a function (such as acos), the "IEEE754 core function" version is to be
used (residing in a file whose name begins with the letter e).
A complete and self-contained description of the algorithms to be used for these functions will be provided in a future version of this specification. It is also anticipated that the algorithms will be coded in Java to provide a reference implementation that is not tied to fdlibm.
20.11.1 public static final double E = 2.7182818284590452354;
The constant value of this field is the double value that is closer than any other
to e, the base of the natural logarithms.
20.11.2 public static final double PI = 3.14159265358979323846;
The constant value of this field is the double value that is closer than any other
to 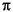 , the ratio of the circumference of a circle to its diameter.
, the ratio of the circumference of a circle to its diameter.
20.11.3 public static double sin(double a)
This method computes an approximation to the sine of the argument, using the
sin algorithm as published in fdlibm (see the introduction to this section).
20.11.4 public static double cos(double a)
This method computes an approximation to the cosine of the argument, using the
cos algorithm as published in fdlibm (see the introduction to this section).
20.11.5 public static double tan(double a)
This method computes an approximation to the tangent of the argument, using the
tan algorithm as published in fdlibm (see the introduction to this section).
20.11.6 public static double asin(double a)
This method computes an approximation to the arc sine of the argument, using the
asin algorithm as published in fdlibm (see the introduction to this section).
20.11.7 public static double acos(double a)
This method computes an approximation to the arc cosine of the argument, using
the acos algorithm as published in fdlibm (see the introduction to this section).
20.11.8 public static double atan(double a)
This method computes an approximation to the arc tangent of the argument, using
the atan algorithm as published in fdlibm (see the introduction to this section).
20.11.9 public static double atan2(double y, double x)
This method computes an approximation to the arc tangent of the quotient 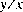 of
the arguments, using the a
of
the arguments, using the atan2 algorithm as published in fdlibm (see the introduction to this section).
double value closest to  .
.
double value closest to 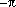 .
.
double value closest to  .
.
double value closest to 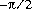 .
.
double value closest to 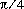 .
.
double value closest to 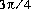 .
.
double value closest to 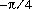 .
.
double value closest to 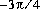 .
.
20.11.10 public static double exp(double a)
This method computes an approximation to the exponential function of the argument (e raised to the power of the argument, where e is the base of the natural logarithms (§20.11.1)), using the exp algorithm as published in fdlibm (see the
introduction to this section).
20.11.11 public static double log(double a)
This method computes an approximation to the natural logarithm of the argument,
using the log algorithm as published in fdlibm (see the introduction to this section).
20.11.12 public static double sqrt(double a)
Whan that Aprill with his shoures soote
The droghte of March hath perced to the roote . . .
—Geoffrey Chaucer (1328-1400), The Canterbury Tales, General Prologue
This method computes an approximation to the square root of the argument.
Otherwise, the result is the double value closest to the true mathematical square
root of the argument value.
20.11.13 public static double pow(double a, double b)
This method computes an approximation to the mathematical operation of raising
the first argument to the power of the second argument, using the pow algorithm as
published in fdlibm (see the introduction to this section).
1.0.
1.0, then the result is the same as the first argument.
double value.
(In the foregoing descriptions, a floating-point value is considered to be an integer
if and only if it is a fixed point of the method ceil (§20.11.15) or, which is the
same thing, a fixed point of the method floor (§20.11.16). A value is a fixed
point of a one-argument method if and only if the result of applying the method to
the value is equal to the value.)
20.11.14 public static double IEEEremainder(double x, double y)
This method computes the remainder operation on two arguments as prescribed
by the IEEE 754 standard: the remainder value is mathematically equal to
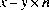 where
where  is the mathematical integer closest to the exact mathematical
value of the quotient
is the mathematical integer closest to the exact mathematical
value of the quotient 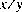 ; if two mathematical integers are equally close to
; if two mathematical integers are equally close to 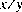 then n is the integer that is even. If the remainder is zero, its sign is the same as the
sign of the first argument.
then n is the integer that is even. If the remainder is zero, its sign is the same as the
sign of the first argument.
20.11.15 public static double ceil(double a)
The result is the smallest (closest to negative infinity) double value that is not less
than the argument and is equal to a mathematical integer.
-1.0, then the result is negative zero.
Note that the value of Math.ceil(x) is exactly the value of -Math.floor(-x).
20.11.16 public static double floor(double a)
The result is the largest (closest to positive infinity) double value that is not
greater than the argument and is equal to a mathematical integer.
20.11.17 public static double rint(double a)
The result is the double value that is closest in value to the argument and is equal
to a mathematical integer. If two double values that are mathematical integers are
equally close to the value of the argument, the result is the integer value that is
even.
20.11.18 public static int round(float a)
Round numbers are always false.
—Samuel Johnson (1709-1784)
The result is rounded to an integer by adding 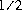 , taking the floor of the result,
and casting the result to type
, taking the floor of the result,
and casting the result to type int.
In other words, the result is equal to the value of the expression:
(int)Math.floor(a + 0.5f)
0.
Integer.MIN_VALUE (§20.7.1), the result is equal to the value of Integer.MIN_VALUE.
Integer.MAX_VALUE (§20.7.2), the result is equal to the value of Integer.MAX_VALUE.
20.11.19 public static long round(double a)
The result is rounded to an integer by adding 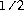 , taking the floor of the result,
and casting the result to type
, taking the floor of the result,
and casting the result to type long.
In other words, the result is equal to the value of the expression:
(long)Math.floor(a + 0.5d)
0.
Long.MIN_VALUE (§20.7.1), the result is equal to the value of Long.MIN_VALUE.
Long.MAX_VALUE (§20.7.2), the result is equal to the value of Long.MAX_VALUE.
20.11.20 public static double random()
The result is a double value with positive sign, greater than or equal to zero but
less than 1.0, chosen pseudorandomly with (approximately) uniform distribution
from that range.
When this method is first called, it creates a single new pseudorandom-number generator, exactly as if by the expression
new java.util.Random()
This new pseudorandom-number generator is used thereafter for all calls to this method and is used nowhere else.
This method is properly synchronized to allow correct use by more than one thread. However, if many threads need to generate pseudorandom numbers at a great rate, it may reduce contention for each thread to have its own pseudorandom number generator.
20.11.21 public static int abs(int a)
The result is the absolute value of the argument, if possible.
If the argument is not negative, the argument is returned.
If the argument is negative, the negation of the argument is returned. Note that if the argument is equal to the value of Integer.MIN_VALUE (§20.7.1), the most negative representable int value, the result will be that same negative value.
20.11.22 public static long abs(long a)
The result is the absolute value of the argument, if possible.
If the argument is not negative, the argument is returned.
If the argument is negative, the negation of the argument is returned. Note that if the argument is equal to the value of Long.MIN_VALUE (§20.8.1), the most negative representable long value, the result will be that same negative value.
20.11.23 public static float abs(float a)
The argument is returned with its sign changed to be positive.
In other words, the result is equal to the value of the expression:
Float.intBitsToFloat(0x7fffffff & Float.floatToIntBits(a))
[This specification for the method abs is scheduled for introduction in Java version 1.1. In previous versions of Java, abs(-0.0f) returns -0.0f, which is not correct.]
20.11.24 public static double abs(double a)
The argument is returned with its sign changed to be positive.
In other words, the result is equal to the value of the expression:
Double.longBitsToDouble((Double.doubleToLongBits(a)<<1)>>>1)
[This specification for the method abs is scheduled for introduction in Java version 1.1. In previous versions of Java, abs(-0.0d) returns -0.0d, which is not correct.]
20.11.25 public static int min(int a, int b)
E duobus malis minimum eligendum.
—Marcus Tullius Cicero (106-43 B. C.), De officiis, iii
The result is the smaller of the two arguments-that is, the one closer to the value
of Integer.MIN_VALUE (§20.7.1). If the arguments have the same value, the
result is that same value.
20.11.26 public static long min(long a, long b)
Of harmes two the lesse is for to cheese.
—Geoffrey Chaucer (1328-1400), Troilus and Criseyde, Book ii
The result is the smaller of the two arguments-that is, the one closer to the value
of Long.MIN_VALUE (§20.8.1). If the arguments have the same value, the result is
that same value.
20.11.27 public static float min(float a, float b)
Of two evils, the less is always to be chosen.
—Thomas a Kempis (1380-1471), Imitation of Christ, Book iii, chapter 12
The result is the smaller of the two arguments-that is, the one closer to negative infinity. If the arguments have the same value, the result is that same value.
[This specification for the method min is scheduled for introduction in Java version 1.1. In previous versions of Java, min(0.0f, -0.0f) returns 0.0f, which is not correct.]
20.11.28 public static double min(double a, double b)
Of two evils I have chose the least.
—Matthew Prior (1664-1721), Imitation of Horace
The result is the smaller of the two arguments-that is, the one closer to negative infinity. If the arguments have the same value, the result is that same value.
[This specification for the method min is scheduled for introduction in Java version 1.1. In previous versions of Java, min(0.0d, -0.0d) returns 0.0d, which is not correct.]
20.11.29 public static int max(int a, int b)
The result is the larger of the two arguments-that is, the one closer to the value of
Integer.MAX_VALUE (§20.7.2). If the arguments have the same value, the result
is that same value.
20.11.30 public static long max(long a, long b)
The result is the larger of the two arguments-that is, the one closer to the value of
Long.MAX_VALUE (§20.8.2). If the arguments have the same value, the result is
that same value.
20.11.31 public static float max(float a, float b)
The result is the larger of the two arguments-that is, the one closer to positive infinity. If the arguments have the same value, the result is that same value.
[This specification for the method max is scheduled for introduction in Java version 1.1. In previous versions of Java, max(-0.0f, 0.0f) returns -0.0f, which is not correct.]
20.11.32 public static double max(double a, double b)
The result is the larger of the two arguments-that is, the one closer to positive infinity. If the arguments have the same value, the result is that same value.
[This specification for the method
max is scheduled for introduction in Java version 1.1.
In previous versions of
Java, max(-0.0d, 0.0d) returns -0.0d, which is not correct.].
In mathematics he was greater
Than Tycho Brahe or Erra Pater
For he, by geometric scale,
Could take the size of pots of ale;
Resolve, by sines and tangents straight
Whether bread or butter wanted weight;
And wisely tell what hour o' the day
The clock does strike, by algebra.
—Samuel Butler, Hudibras, Part I, canto i