| Matika krokem - 4.lekce ... |
|
Komplexní čísla 4.lekce - Goniometrický tvar komplexního čísla, Moivreova věta |
Vytisknout |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A. Výklad a ukázkové příklady Goniometrický tvar komplexního čísla Bod Z - obraz komplexního čísla z = a + bi v Gaussově rovině - můžeme určit také pomocí jeho vzdálenosti r od počátku a velikosti orientovaného úhlu j: 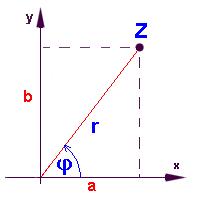 Platí:
Číslo z lze tedy zapsat: z = a + bi = r . cos j + r . sin j . i = r(cos j + i.sin j) Reálné číslo j (určující velikost orientovaného úhlu) nazýváme argument komplexního čísla. Reálné číslo r je absolutní hodnota komplexního čísla. r = |z| =  Goniometrický tvar komplexního čísla z  0 je jeho vyjádření ve tvaru:
Při převodu kompl.čísla do goniometrického tvaru musíme tedy určit nejprve absolutní hodnotu a argument a potom dosadit do předchozího zápisu. Při výpočtu argumentu je dobré využít geometrického znázornění. Příklad 1 Vyjádřete v goniometrickém tvaru číslo z = 3i. 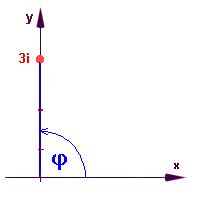 z = 3.(cos p/2 + i.sin p/2) resp. z = 3.(cos 90` + i.sin 90`) Příklad 2 Vyjádřete v goniometrickém tvaru číslo z = 1 - i. 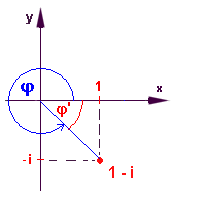  Argument: pomocný ostrý úhel j' je z obrázku p/4 (45`) a argument tedy je j = 2p - p/4 = 7p/4 (315`) Goniometrický tvar čísla z je tedy: z = (cos 7p/4 + i.sin 7p/4) Příklad 3 Vyjádřete v goniometrickém tvaru číslo z = -1 + i 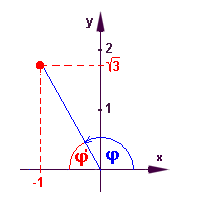 . Argument: U komplexníxh čísel, kde argument nemůžeme určit z obrázku bez výpočtu, postupujeme takro:
Goniometrický tvar čísla z je tedy: z = 2(cos 2p/3 + i.sin 2p/3) Při obráceném převodu (z goniometrického tvaru do algebraického tvaru) vyčíslíme hodnoty goniometrických funkcí a odstraníme závorky. Příklad 4 Vyjádřete v algebraickém tvaru číslo z = 4(cos p/6 + i.sin p/6) = 4( /2 + i.1/2) =
2 + 2iSoučin a podíl komplexních čísel v goniometrickém tvaru V goniometrickém tvaru se snadno určí součin a podíl komplexníxh čísel. Součin libovolných nenulových komplexníxh čísel z1 = |z1|(cos j1 + i.sin j1) a z2 = |z2|(cos j2 + i.sin j2) je rovno komplexnímu číslu :
Podíl libovolných nenulových komplexníxh čísel z1 = |z1|(cos j1 + i.sin j1) a z2 = |z2|(cos j2 + i.sin j2) je rovno komplexnímu číslu :
Příklad 5 Vypočtěte součin z1 . z2 a podíl z1 / z2 komplexních čísel: z1 = (cos p/6 + i.sin p/6) ,
z2 = (cos 5p/6 + i.sin 5p/6)z1 . z2 = .[cos(p/6+5p/6)
+i.sin(p/6+5p/6)] = 2(cos p + i.sin p) = -2z1 / z2 = /[cos(p/6-5p/6)
+i.sin(p/6-5p/6)] = cos (-4p/6) + i.sin (-4p/6) =
cos (4p/3) + i.sin (4p/3) = - /2 - i.1/2Mocnina komplexního čísla Zobecněním předchozích pravidel lze dokázat pravidlo pro celou mocninu komplexního čísla: Pro každé celé číslo n a každé komplexní číslo z = |z|.(cos j + i.sin p) platí:
Pro komplexní jednotku (|z|=1) a přirozený exponent dostáváme větu, kterou odvodil již v 18.století francouzský matematik A.de Moivre: Moivreova věta Pro každé přirozené číslo n a libovolné reálné číslo j platí:
Příklad 6 Vypočtěte (cos p/6 + i.sin p/6)14 = cos 14p/6 + i.sin 14p/6 = cos 7p/3 + i.sin 7p/3 = cos p/3 + i.sin p/3 = 1/2 + i. /2Příklad 7 Pomocí Moivreovy věty vyjádřete sin3x pomocí mocnin sinx a cosx. (cosx + i.sinx)3 = cos3x + i.sin3x užitím vzorce (a + b)3 dostáváme: cos3x + i.3cos2xsinx - 3cosxsin2x - i.sin3x = cos3x + i. sin3x a tedy pro imaginární části musí platit: sin3x = 3cos2xsinx - sin3x = 3(1-sin2x).sinx - sin3x = 3sinx - 4sin3x a pro reálné části: cos3x = cos3x - 3cosx.sin2x = cos3x - 3cosx.(1-cos2x) = cos3x - 3cosx + 3cos3x = 4cos3x - 3cosx Příklad 8 Vypočtěte:  Nejprve upravíme zlomek a převedeme do goniometrického tvaru:  a nyní umocníme: 
B. Příklady s krokovou kontrolou e-učitele C. Příklady na procvičení učiva Na následujících příkladech s výsledky se můžete zdokonalit ve znalostech učiva této lekce. Pokud si nevíte s příkladem rady, užijte stručné nápovědy - Help.
D. Kontrolní test E. Hodnocení výsledků a komunikace s učitelem (tutorem) Komunikace s učitelem (tutorem): Tato část je určena pouze pro registrované uživatele. Zaregistrujte se! |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
)-50
x
+ 
