CESTA K JADERNÉ ENERGII
Lze tedy uvolnit alespoň malou část obrovské klidové energie látky, která je
soustředěna v jádrech atomů - jaderné energie?
Pokusy a pozorování krátce po objevení radioaktivity
v roce 1896 ukázaly, že se při rozpadu nestabilních (radioaktivních) atomů uvolňuje
energie. Množství energie, které získáme při radioaktivním rozpadu; je však pro
praktické využití bezvýznamné. Například přirozeným rozpadem jednoho kilogramu
radia se uvolní přibližně tolik energie, kolik odpovídá spálení 60 tun uhlí.
Rozpad však probíhá velmi pomalu polovina určitého počátečního množství radia
se rozpadne teprve za 1620 let.
Vraťme se nyní ještě jednou k F. W. Astonovi. Jeho přesná měření na hmotnostním
spektrografu ukázala, že vazebná energie je u jader jednotlivých prvků a jejich izotopů různá. Je zřejmé, že čím více nukleonů je v jádře, tím větší bude
vazebná energie. Závislost vazebné energie na počtu nukleonů v jádře však není
lineární. Odchylku způsobují efekty související jak se strukturou jader, tak i s
elektrostatickým odpuzováním kladně nabitých protonů.
Zobrazíme si graficky střední vazebnou energii (tj. vazebnou energii
připadající na jeden nukleon) v závislosti na počtu nukleonů.
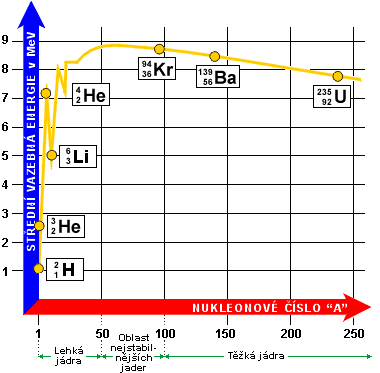 |
Graf závislosti střední
vazebné energie
na nukleonovém čísle A. |
Na tomto grafu lépe vyniknou všechny odchylky od lineárního průběhu hodnoty
střední vazebné energie nejprve rychle rostou od 0 (pro A=1) do 8 MeV (pro A=16), pak
jsou zhruba stejně velké s maximem o hodnotě 8,6 MeV (pro A=60, tj. 58Fe, 62Ni)
a nakonec pomalu klesají do 7,6 MeV pro nejtěžší jádra.
Skutečnost, že těžká jádra jsou méně stabilní, je třeba vztáhnout k tomu, že
při zvyšování počtu nukleonů sice přitažlivé jaderné síly v jádře
narůstají, ale působí pouze mezi sousedními nukleony. Odpudivé síly mezi protony
rovněž narůstají, působí však mezi všemi protony. Tím se vazba mezi částicemi
poněkud uvolní.
Nejdůležitějším závěrem je však pro nás možnost využití jaderné energie: z
grafu plyne, že jadernou energii můžeme uvolňovat dvěma způsoby štěpením (viz
konec grafu) a slučováním (viz začátek grafu).
Štěpení
První možností je štěpení
těžkých jader na středně těžká. Podle grafu jsou produkty štěpení
stabilnější a celková vazebná energie (která se uvolní při jejich vzniku) je
větší než vazebná energie těžkého jádra. Proto mohou těžká jádra štěpením
přecházet do stavu s nižší klidovou energií a přitom se uvolňuje poměrně velká
energie ve formě kinetické energie produktů štěpení kladně nabitá jádra jsou
svým elektrickým polem odmrštěna od sebe a při zabrzdění těchto částic v palivu,
moderátoru a v ostatních částech reaktoru přejde jejich kinetická energie
postupně až na energii kmitů atomů a molekul, tedy do formy tepelné energie. Z grafu
vidíme, že se přitom uvolní asi 1 MeV na nukleon. Při jednom procesu štěpení
těžkého jádra se tak uvolní okolo 200 MeV, což je podle Einsteinova vztahu v
jednotkách u asi 200/931,494 = 0,21 u. Z kapkového modelu atomových jader plyne,
že štěpení je energeticky výhodné, je-li parametr štěpení Z2/A >
17. Tato podmínka je splněna pro všechna jádra těžší než Ag. Prakticky je však
štěpení možné pouze pro jádra s A > 230 (Th, U, Pu). Největší průmyslový
význam má v současné době štěpení jader uranu 235U v lehkovodních reaktorech.
Jaká část klidové energie se uvolní? Tento podíl jednoduše spočítáme,
vyjádříme-li klidovou hmotnost uranu v jednotkách u. S jistou chybou lze
hmotnost nukleonu považovat za 1 u. Pak 235U má hmotnost asi 235 u.
Uvolněná klidová energie 0,21 u/235 u = 8,9.10-4 odpovídá
asi 0,1 % klidové energie 235U.
Slučování
Druhou možností, jak získat energii, je slučování velmi lehkých jader
na jádra těžší (termojaderná syntéza). Z našeho grafu je zřejmé, že sloučením
dvou lehkých jader (např. 2/1H a 3/1H) s
nízkou vazebnou energií vznikne stabilní jádro s vysokou vazebnou energií.
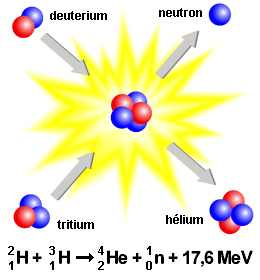 |
| Schéma jaderného slučování
(fúze). Znázorněná reakce probíhá velmi rychle. Tuto reakci budou pravděpodobně
využívat první energetické termojaderné reaktory. Při jaderném slučování se
uvolňuje až 1% klidové energie interagujících částic. |
Jejich rozdíl se přitom uvolní. Reakci můžeme chápat tak, jakoby útvar
složený původně ze dvou jader přešel do nižšího energetického stavu. Z průběhu
grafu střední vazebné energie je zřejmé, že při slučování lehkých jader se
může získat až několikanásobně více energie na nukleon než v případě
jaderného štěpení. Reakce jaderné syntézy jsou základními procesy uvolňování
energie na Slunci a ve hvězdách. Proces vzniku sluneční energie vysvětlil německý
fyzik H. A. Bethe v roce 1938 jako vodíkovou syntézu, při níž se v několika krocích
slučují čtyři vodíková jádra (protony) do jednoho jádra helia: 41/1
® 4/2He + 2 e+ + 2ue + 2g + 26,72 MeV. Z hlediska
našich měřítek je energetická bilance Slunce skutečně úctyhodná: každou vteřinu
se jadernými silami mění 0,5 miliardy tun vodíku v helium s celkovým hmotnostním
úbytkem 4 miliony tun. Celkový uvolňovaný výkon je 3,6.1026 W! A přitom
je naše Slunce ve srovnání s ostatními hvězdami docela malé...
Jaká část klidové energie se při této reakci uvolňuje? Při jedné reakci syntézy
se uvolní 26,7 MeV, což je v atomových hmotnostních jednotkách 26,7/931,494 =
0,029 u.
Klidová hmotnost 4 vodíkových jader 1/1H je přibližně 4 u.
Pak uvolněná klidová energie 0,029 u/4 u = 7,25. 10-3
odpovídá 0,7 % klidové energie slučovaných částic.
Pro budoucí řízené uvolňování energie v termojaderných reaktorech mají význam
jiné reakce, např. 2/1H + 2/1H ® 3/2He +1/0n +
3,26 MeV. Tato reakce probíhá mnohem rychleji než syntéza na Slunci, což je
důležité vzhledem k nutnosti udržet v termojaderných reaktorech po určitou dobu
velice horké husté plazma pro nastartování
reakce. Těžký vodík 2/1H (deuterium) máme ve světových
mořích k dispozici v prakticky nevyčerpatelném množství.
|

 Aktuálne
Encyklopedie energie
Soutež
Bheliom
Aktuálne
Encyklopedie energie
Soutež
Bheliom 
