Java a 3D grafika - Geometry (PointArray, LineArray a TriangleArray)
V tomto Φlßnku se zaΦneme zab²vat vytvß°enφm objekt∙ prost°ednictvφm instancφ t°φdy Shape3D. Ukß₧eme si, jak pomocφ ·seΦek vytvo°it drßtov² model krychle, a pak si povφme, jak se dajφ pomocφ troj·helnφk∙ vytvß°et t∞lesa se st∞nami.
Ne₧ se pustφte do Φtenφ tohoto Φlßnku, doporuΦuji vßm o₧ivit si pov∞domφ o tom, jakΘ objekty se objevujφ v grafu scΘny, jakΘ podmφnky musφ graf scΘny spl≥ovat a k Φemu jsou dobrΘ objekty Appearance, prost°ednictvφm Φlßnku Java a 3D grafika - graf scΘny.
Pro vytvß°enφ trojrozm∞rn²ch objekt∙ se pou₧φvajφ objekty Shape3D, kterΘ mohou odkazovat na instance podt°φd abstraktnφ t°φdy Geometry a na objekty Appearance. (Jeden objekt Shape3D m∙₧e odkazovat i na n∞kolik objekt∙ Geometry, ale ty musφ b²t stejnΘho typu.) Tyto objekty se jim p°i°azujφ bu∩ p°φmo v konstruktoru Shape3D(Geometry geometry, Appearance appearance), nebo pomocφ metod setGeometry(Geometry geometry) a setAppearance(Appearance appearance).
Objekty Geometry obsahujφ vlastnφ data objekt∙, tedy sou°adnice vrchol∙, normßlovΘ vektory, barvy vrchol∙ a sou°adnice slou₧φcφ k otexturovßnφ. V objektech Appearance pak jsou ulo₧eny informace o materißlu, Üφ°ce Φar, tlouÜ¥ce bod∙, o tom, zda se mß nebo nemß pou₧φt antialiasing a tak dßle. Podrobn∞ji jsme se ale t°φd∞ Appearance v∞novali v Φlßnku o grafick²ch primitivech, tak₧e na tomto mφst∞ snad postaΦφ jen tato krßtkß zmφnka.
T°φda GeometryArray a jejφ potomci
Vzhledem k tomu, ₧e t°φd odvozen²ch od t°φdy Geometry je pom∞rn∞ dost, rozlo₧φme si povφdßnφ o nich do n∞kolika Φlßnk∙. V tomto Φlßnku zaΦneme n∞kolika potomky t°φdy GeometryArray, konkrΘtn∞ t°φdami PointArray, LineArray a TriangleArray.
JednoduÜÜφ verze konstruktor∙ vÜech Φty° zmφn∞n²ch t°φd p°ebφrajφ pouze dva parametry - poΦet vrchol∙ a jejich "formßt", tedy bitovΘ p°φznaky °φkajφcφ, co p°esn∞ bude v danΘm objektu Geometry ulo₧eno. P°φznaky definovanΘ ve t°φd∞ GeometryArray jsou COORDINATES pro sou°adnice, NORMALS pro normßlovΘ vektory, COLOR_3 pro barvu bez alfa-transparence, COLOR_4 pro barvu s alfa-transparencφ, TEXTURE_COORDINATES_2, TEXTURE_COORDINATES_3 a TEXTURE_COORDINATES_4 pro sou°adnice textur. Tak nap°φklad budeme-li chtφt vytvo°it instanci t°φdy PointArray obsahujφcφ Φty°i barevnΘ body, bude volßnφ konstruktoru vypadat takto: PointArray(4, GeometryArray.COORDINATES | GeometryArray.COLOR_3);.
Mßme-li u₧ objekt GeometryArray vytvo°en², musφme do n∞ho vlo₧it pot°ebnß data. Nßsledujφ metody slou₧φcφ pro nastavenφ sou°adnic vrchol∙:
- public void setCoordinates(int index, float[] coordinates)
- public void setCoordinates(int index, double[] coordinates)
- public void setCoordinates(int index, Point3f[] coordinates)
- public void setCoordinates(int index, Point3d[] coordinates)
V poli "coordinates" jsou ulo₧eny sou°adnice vrchol∙. Parametr "index" oznaΦuje pozici v poli "coordinates", kde se sou°adnice nachßzejφ. Metody pro nastavenφ barev, normßlov²ch vektor∙ a sou°adnic textur jsou velice podobnΘ a postupn∞ se k nim dostaneme alespo≥ v p°φkladech.
T°φda LineArray
Nynφ u₧ toho vφme dost na to, abychom mohli s vyu₧itφm t°φdy LineArray, kterß je urΦena k vytvß°enφ t∞les z ·seΦek, vytvo°it jednoduchou t°φdu odvozenou od t°φdy Shape3D slou₧φcφ k vytvß°enφ drßtov²ch krychlφ. Jejφ k≤d nßsleduje:
import javax.media.j3d.*;
public class DratovaKrychle extends Shape3D {
float souradnice[] =
//sou°adnice bod∙, v₧dy dva body pro ·seΦku
{-1,-1,1, -1,1,1, -1,1,1, 1,1,1,
1,1,1, 1,-1,1, 1,-1,1, -1,-1,1,
-1,-1,-1, -1,1,-1, -1,1,-1, 1,1,-1,
1,1,-1, 1,-1,-1, 1,-1,-1, -1,-1,-1,
-1,-1,1, -1,-1,-1, -1,1,1, -1,1,-1,
1,1,1, 1,1,-1, 1,-1,1, 1,-1,-1};
public DratovaKrychle(float hrana) {
//nastavφme velikost hran
for (int i = 0; i < 72; i++)
souradnice[i] *= hrana/2f;
setGeometry(vytvorGeometry());
setAppearance(vytvorAppearance());
}
Geometry vytvorGeometry(){
//vytvo°φme instanci t°φdy LineArray
LineArray lineArray = new LineArray(24, GeometryArray.COORDINATES);
//nastavφme sou°adnice
lineArray.setCoordinates(0, souradnice);
return lineArray;
}
Appearance vytvorAppearance(){
Appearance app = new Appearance();
//nastavφme tlouÜ¥ku Φßry na 3 pixely, povolφme antialiasing
LineAttributes la = new LineAttributes(3, LineAttributes.PATTERN_SOLID, true);
app.setLineAttributes(la);
return app;
}
}
Jak m∙₧ete sami vid∞t, je k≤d tΘto t°φdy velice jednoduch². Pouze v konstruktoru vytvß°φ objekt Geometry, do kterΘho vlo₧φ sou°adnice zadanΘ v poli "souradnice", kterΘ jeÜt∞ p°edtφm vynßsobφ parametrem "hrana/2", abychom mohli vytvß°et krychle r∙zn²ch velikostφ. Toto je v²sledek:
Pou₧itφ tΘto t°φdy a takΘ dalÜφch t°φd v tomto Φlßnku, krom∞ t°φdy PointArray, je mnohdy dost ne·spornΘ z hlediska nßrok∙ na pam∞¥ û nap°φklad sou°adnice ka₧dΘho z vrchol∙ krychle v p°φkladu uklßdßme t°ikrßt. ╪eÜenφm mohou b²t podt°φdy, bu∩ t°φdy GeometryStripArray nebo t°φdy IndexedGeometryArray. O tom ale a₧ jindy.
T°φda PointArray
T°φda PointArray nßm umo₧≥uje zobrazovat jednotlivΘ vrcholy. Ve spojenφ s nφ se hodφ vyu₧φt mo₧nosti nastavenφ tlouÜ¥ky bod∙ prost°ednictvφm t°φdy PointAttributes, jejφ₧ instance se p°ipojujφ k p°φsluÜn²m objekt∙m Appearance. Konstruktor PointAttributes(float pointSize, boolean antialiasing) p°ebφrß dva parametry. Parametr "pointSize" urΦuje tlouÜ¥ku bod∙ a parametr "antialiasing" urΦuje, jestli se mß pou₧φt antialiasing.
T°φdu PointArray vyu₧ijeme k vylepÜenφ p°edchozφho p°φkladu tφm, ₧e do ka₧dΘho vrcholu krychle nakreslφme bod zadanΘ tlouÜ¥ky. NaÜe novß t°φda vÜak nebude rozÜi°ovat t°φdu Shape3D, ale bude odvozena od t°φdy Group (kv∙li nemo₧nosti vklßdat do objekt∙ Shape3D objekty Geometry r∙znΘho typu, v tomto p°φpad∞ tedy instance t°φd LineArray a PointArray).
import javax.media.j3d.*;
public class DratovaKrychle2 extends Group {
float souradnice[] =
{1,1,1, -1,1,1, 1,-1,1, 1,1,-1,
-1,-1,1, -1,1,-1, 1,-1,-1, -1,-1,-1};
public DratovaKrychle2(float hrana) {
for (int i = 0; i < 24; i++)
souradnice[i] *= hrana/2f;
Shape3D shape2 = new Shape3D();
//objektu shape2 nastavφme objekt Geometry
shape2.setGeometry(vytvorGeometryBodu());
//objektu shape2 nastavφme objekt Appearance
shape2.setAppearance(vytvorAppearanceBodu());
//p°idßme objekt DratovaKrychle
addChild(new DratovaKrychle(hrana));
addChild(shape2);
}
Geometry vytvorGeometryBodu(){
PointArray pointArray = new PointArray(8, GeometryArray.COORDINATES);
pointArray.setCoordinates(0, souradnice);
return pointArray;
}
Appearance vytvorAppearanceBodu(){
Appearance app = new Appearance();
PointAttributes pa = new PointAttributes(10, true);
app.setPointAttributes(pa);
return app;
}
}
A takto vypadß v²sledek:
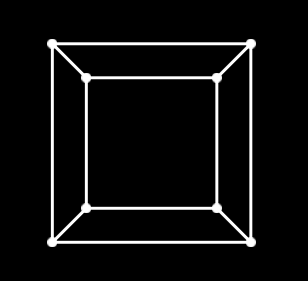
Pro lepÜφ p°edstavu si jeÜt∞ ukß₧eme, jak by mohla vypadat instance tΘto t°φdy zakreslenß v grafu scΘny, jak to m∙₧ete vid∞t na nßsledujφcφm obrßzku:
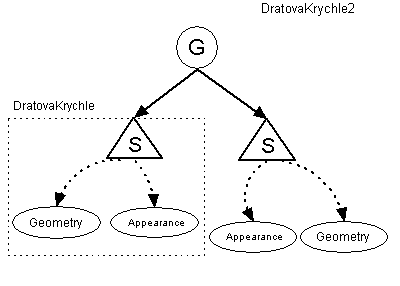
T°φda TriangleArray
T°φda TriangleArray slou₧φ, jak u₧ jejφ nßzev napovφdß, k vytvß°enφ t∞les z troj·helnφk∙. Jejφ vyu₧itφ si ukß₧eme na vytvo°enφ Φty°st∞nu. Abychom si takΘ ukßzali, jak pracovat s barvami p°i°azen²mi jednotliv²m vrchol∙m, o₧ivφme st∞ny naÜeho Φty°st∞nu nßhodn∞ vybran²mi barvami.
import javax.media.j3d.*;
import javax.vecmath.*;
import java.util.Random;
public class Ctyrsten extends Shape3D {
//vypoΦφtßme si dv∞ odmocniny, kterΘ budeme pot°ebovat
float s6 = (float)Math.sqrt(6);
float s3 = (float)Math.sqrt(3);
//ka₧dß °ßdka odpovφdß jednomu troj·helnφku
float souradnice[] = {
-0.5f,0,-s3/6f, 0,0,s3/3f, 0.5f,0,-s3/6f,
-0.5f,0,-s3/6f, 0,s6/3f,0, 0,0,s3/3f,
0,0,s3/3f, 0,s6/3f,0, 0.5f,0,-s3/6f,
0.5f,0,-s3/6f, 0,s6/3f,0, -0.5f,0,-s3/6f};
public Ctyrsten(float hrana) {
for (int i = 0; i < 36; i++)
souradnice[i] *= hrana;
setGeometry(vytvorGeometry());
}
Geometry vytvorGeometry(){
TriangleArray ta = new TriangleArray(12, GeometryArray.COORDINATES | GeometryArray.COLOR_3);
ta.setCoordinates(0,souradnice);
//obarvφme st∞ny nßhodn∞ vybran²mi barvami
Random rand = new Random();
for (int i = 0; i < 4; i++){
Color3f color = new Color3f(rand.nextFloat(), rand.nextFloat(), rand.nextFloat());
for (int j = 0; j < 3; j++)
ta.setColor(3*i+j, color);
}
return ta;
}
}
Obarvenφ tohoto t∞lesa provßdφme v metod∞ vytvorGeometry(), kde volßnφm metody setColor(int i, Color3f color) nastavujeme ka₧d²m t°em bod∙m urΦujφcφm st∞nu jednu nßhodn∞ vybranou barvu. Barvy jsme ale klidn∞ mohli nastavit odliÜnΘ pro ka₧d² vrchol - pak by se v jednotliv²ch st∞nßch postupn∞ m∞nily.
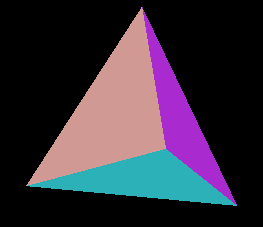
Objekty, kterΘ jsme v tomto Φlßnku vytvo°ili, majφ jeden velk² nedostatek - sv∞tla na n∞ nemajφ ₧ßdn² ·Φinek. Jak se s tφmto nedostatkem vypo°ßdat, o tom si povφme p°φÜt∞.
