Java a 3D grafika - graf scΘny
V p°edchozφm Φlßnku jsme si ukßzali, jak se s pomocφ Java 3D API vytvß°φ jednoduchß scΘna. V tomto Φlßnku se podφvßme podrobn∞ji na problematiku grafu scΘny. Ukß₧eme si, jak jej zakreslovat a seznßmφme se s bßzov²mi t°φdami v∞tÜiny objekt∙ objevujφcφch se ve scΘn∞.
Jak zakreslovat graf scΘny
Jak znßmo, dokß₧e obΦas jeden obrßzek osv∞tlit urΦitou problematiku daleko lΘpe ne₧ n∞kolik desφtek °ßdk∙ textu a v p°φpad∞ grafu scΘny to platφ dvojnßsob. Jen si zkuste p°edstavit, jak slovy popisujete nßsledujφcφ jednoduch² graf:
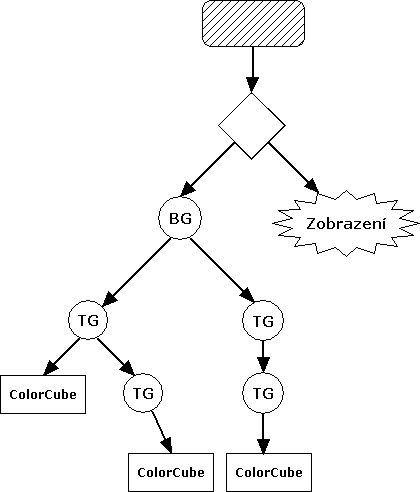
A to obsahuje pouze t°i barevnΘ krychle (ColorCube), z nich₧ dv∞ jsou transformovßny jednφm spoleΦn²m objektem TransformGroup, z Φeho₧ jedna je transformovßna jeÜt∞ dalÜφm objektem TransformGroup, a t°etφ je transformovßna jin²mi dv∞ma objekty TransformGroup.
A te∩ popravd∞. ╚emu jste rozum∞li lΘpe? Obrßzku, p°esto₧e jste v n∞m neznali nejmΘn∞ polovinu pou₧it²ch symbol∙, nebo p°edchßzejφcφmu zmatenΘmu textu? A co teprve, kdybyste v obrßzku v²znam vÜech symbol∙ znali? Myslφm si, ₧e obrßzek vyhrßvß.
Nynφ si poj∩me vysv∞tlit v²znam pou₧it²ch symbol∙. Nßsledujφcφ obrßzek je vÜechny shrnuje. (Tento zp∙sob zßpisu je p°evzat z oficißlnφho tutorißlu.)
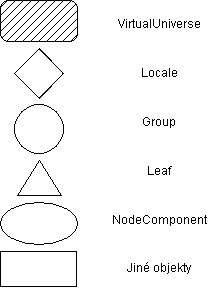
Se t°φdami VirtualUniverse a Locale jsme se seznßmili ji₧ minule. Te∩ je na Φase vysv∞tlit si, k Φemu slou₧φ ty zb²vajφcφ. Instance t°φd odvozen²ch od prvnφ z nich, t°φdy Group, majφ v grafu, °eΦeno slovy klasickΘ terminologie pro popis strom∙, roli uzl∙, tzn. mohou mφt pouze jednoho rodiΦe a neomezen∞ potomk∙.
T°φda Leaf je nadt°φdou pro t°φdy, jejich₧ instance jsou v danΘm stromu listy, co₧ znamenß, ₧e u₧ nemajφ ₧ßdnΘ dalÜφ potomky. P°φkladem m∙₧e b²t t°φda ColorCube, se kterou jsme se seznßmili v minulΘm Φlßnku a se kterou pracujeme i dnes.
Mo₧nß vßs nynφ napadß otßzka, proΦ jsou v ukßzkovΘm grafu objekty ColorCube zobrazeny jako obdΘlnφky a ne jako troj·helnφky, co₧ by podle v²Üe uvedenΘho bylo jist∞ sprßvn∞jÜφ. Inu, tady zase jednou zvφt∞zil pragmatismus nad p°esn²m vyjad°ovßnφm. On toti₧ troj·helnφk nenφ prßv∞ nejvhodn∞jÜφ pro zßpis delÜφho textu. Z toho d∙vodu, pokud nßs bude v budoucnu zajφmat u n∞jakΘho objektu v grafu jeho p°esn² nßzev, zobrazφme jej jako obdΘlnφk.
P°edposlednφ ze symbol∙ v tabulce, ovßl, oznaΦuje instance t°φd, kterΘ jsou odvozeny od t°φdy NodeComponent. Podt°φdami t°φdy NodeComponent jsou nap°φklad t°φdy Appearance a Geometry, se kter²mi se blφ₧e seznßmφme v n∞kterΘm z dalÜφch Φlßnk∙ tΘto sΘrie. Prozatφm snad postaΦφ, kdy₧ si °ekneme, ₧e t°φdy odvozenΘ od tΘto t°φdy nejsou formßln∞ p°φmo souΦßstφ stromu, proto₧e na n∞ odkazujφ objekty list∙ (Leaf), co₧ by jinak nebylo mo₧nΘ (list p°ece nem∙₧e mφt potomky), nejednß se tedy formßln∞ o vztah potomek-rodiΦ.
Äijφcφ a zkompilovanΘ objekty
Vlo₧φme-li objekt BranchGroup do objektu Locale, stanou se tento objekt a objekty v n∞m obsa₧enΘ takzvan∞ ₧iv²mi. To znamenß, ₧e kv∙li v²konu bude graf scΘny p°eveden do v²hodn∞jÜφ podoby, co₧ s sebou nev²hodu v tom, ₧e ji₧ nebudeme moci nadßle p°idßvat objekty do objekt∙ Group nebo m∞nit transformaΦnφ matici v objektech TransformGroup.
Pochopiteln∞ jsou vÜak situace, kdy scΘnu chceme m∞nit i nadßle - a¥ u₧ pot°ebujeme animovat existujφcφ objekty nebo p°idßvat novΘ. Pak musφme n∞jak oznaΦit ty Φßsti scΘny, kterΘ se budou m∞nit. K tomu slou₧φ metody void setCapability(int bit), void clearCapability(int bit) a boolean getCapability(int bit). Parametr bit typu int, p°edßvan² vÜem t∞mto metodßm, nese bitov² p°φznak urΦujφcφ, co je s dan²m objektem (respektive jeho potomky), mo₧nΘ d∞lat. Metoda setCapability(int bit) "zapφnß" tento p°φznak, metoda clearCapability(int bit) tento p°φznak vypφnß a koneΦn∞ metoda getCapability(int bit) vracφ true, pokud je dan² p°φznak nastaven².
Nap°φklad ve t°φd∞ Group jsou definovßny mimo jinΘ nßsledujφcφ p°φznaky: ALLOW_CHILDREN_EXTEND dovolujφcφ p°idßvat dalÜφ objekty do danΘho objektu Group, ALLOW_CHILDREN_READ dovolujφcφ p°istupovat k potomk∙m danΘho objektu a ALLOW_CHILDREN_WRITE umo₧≥ujφcφ upravovat odkazy na potomky tohoto objektu. Ve t°φd∞ TransformGroup jsou pak definovßny dalÜφ p°φznaky: ALLOW_TRANSFORM_READ dovolujφcφ p°istupovat k transformaΦnφ matici a pota₧mo i jejφm jednotliv²m slo₧kßm (rotace, posunutφ) a ALLOW_TRANSFORM_WRITE umo₧≥ujφcφ m∞nit transformaci, co₧ je nezbytnΘ nap°φklad pro animovßnφ. Krom∞ ji₧ zmφn∞n²ch p°φznak∙ vÜak existujφ i dalÜφ, s nimi₧ se setkßme v n∞kterΘm z dalÜφch Φlßnk∙.
Sice je mo₧nΘ renderovat i scΘnu, kterß je pouze ₧ijφcφ, ale pokud chcete v∞tÜφ rychlost, je pot°eba objekty BranchGroup ve scΘn∞ jeÜt∞ navφc "zkompilovat". K tomu slou₧φ metoda compile(), jejφ₧ volßnφ zp∙sobφ dalÜφ zm∞ny v internφ reprezentaci scΘny. Jejφ pou₧φvßnφ je nav²sost u₧iteΦnΘ a neexistuje prakticky ₧ßdn² d∙vod, proΦ ji ignorovat.
Mal² p°φklad
Nynφ si na krßtkΘm p°φkladu ukß₧eme pou₧itφ toho, co jsme se dnes nauΦili. V²sledek nebude nijak osl≥ujφcφ, p∙jde o dalÜφ variaci na tΘma barevnΘ krychle. Nejprve vytvo°φme scΘnu s barevnou krychlφ, jejφm₧ rodiΦem bude objekt TransformGroup, pak ji zkompilujeme a teprve a₧ potom ji budeme transformovat ·pravou objektu TransformGroup, co₧ znamenß, ₧e se nevyhneme pou₧itφ metody setCapability(int bit), co₧ je v podstat∞ hlavnφm ·Φelem tohoto p°φkladu. Celou scΘnu si pro procviΦenφ rovn∞₧ zakreslφme.
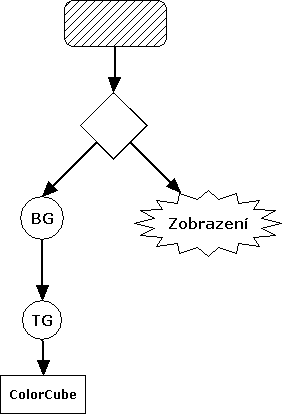
Zde nßsleduje zdrojov² k≤d p°φkladu:
import java.awt.*;
import javax.swing.*;
import com.sun.j3d.utils.universe.*;
import com.sun.j3d.utils.geometry.*;
import javax.media.j3d.*;
import javax.vecmath.*;
public class Capabilities extends JFrame{
TransformGroup tg;
public Capabilities() {
super("Ukßzka pou₧itφ setCapability()");
//Na nßsledujφcφch °ßdcφch vytvo°φme Canvas3D
Container pane = getContentPane();
pane.setLayout(new BorderLayout());
GraphicsConfiguration config = SimpleUniverse.getPreferredConfiguration();
Canvas3D canvas = new Canvas3D(config, false);
pane.add("Center", canvas);
//vytvo°φme objekt SimpleUniverse
SimpleUniverse universe = new SimpleUniverse(canvas);
//nastavφme vzdßlenost pozorovatele od monitoru na 2m
universe.getViewingPlatform().setNominalViewingTransform();
//p°idßme BranchGroup vytvo°en² v metod∞ vytvorBranchGroup()
//do objektu SimpleUniverse
universe.addBranchGraph(vytvorBranchGroup());
//upravφme transformaci v objektu TransformGroup tg,
//kter² je ji₧ souΦßstφ grafu scΘny, co₧ by nebylo mo₧nΘ,
//kdybychom v metod∞ vytvorBranchGroup nevolali
//metodu setCapability s parametrem ALLOW_TRANSFORM_GROUP
tg.setTransform(vytvorTransform());
addWindowListener(new java.awt.event.WindowAdapter() {
public void windowClosing(java.awt.event.WindowEvent evt) {
System.exit(0);
}
});
}
protected BranchGroup vytvorBranchGroup(){
//ko°en tΘto Φßsti scΘny
BranchGroup bg = new BranchGroup();
//tento objekt upravujeme a₧ dßle v konstruktoru
tg = new TransformGroup();
//nastavφme, ₧e chceme nadßle m∞nit transformaΦnφ matici
//tohoto objektu
tg.setCapability(TransformGroup.ALLOW_TRANSFORM_WRITE);
//p°idßme objekt TransformGroup tg jako potomka
//do objektu bg
bg.addChild(tg);
//vlo₧φme jeÜt∞ barevnou krychli jako potomka zmφn∞nΘho
//objektu TransformGroup tg
tg.addChild(new ColorCube(0.3));
//zkompilujeme scΘnu
bg.compile();
return bg;
}
protected Transform3D vytvorTransform(){
Transform3D tr1 = new Transform3D();
//nastavφme ·hel otoΦenφ na 30░
tr1.rotX(Math.PI/6);
//vytvo°φme druhou transformaΦnφ matici
Transform3D tr2 = new Transform3D();
//nastavφme ·hel otoΦenφ na 60░
tr2.rotY(-Math.PI/3);
//vynßsobφme spolu matice
tr2.mul(tr1);
return tr2;
}
public static void main(String[] args){
new Capabilities().show();
}
}
Na tomto p°φkladu sice nenφ u₧iteΦnost popsan²ch technik p°φliÜ z°etelnß, a₧ se ale budeme zab²vat animovßnφm objekt∙, neobejdeme se bez nich. Nßsledujφcφ obrßzek je v²sledkem pou₧itφ p°edchßzejφcφho k≤du:
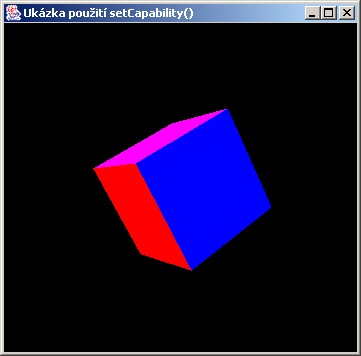
P°φÜt∞ se seznßmφme s t°φdami pro tvorbu geometrick²ch primitiv a ukß₧eme si, jak upravovat jejich vzhled (barvu a dalÜφ vlastnosti) pomocφ objekt∙ Appearance.
