┌vod do kryptografie

Krypotgrafie mß svou dlouhou historii a opravdu se nevyskytuje jen ve filmech agenta 007, ale i v praktickΘm ╛ivot∞. P°edstavte si, ╛e posφlßte kolegovi v prßci seznam zam∞stnanc∙ a jejich platy. Dokument je samoz°ejm∞ tajn² a Vy jej nechcete nechat b∞hat po sφti jen tak. Nebo chcete utajit svΘ dokumenty na poΦφtaΦi, na kter² mß p°φstup kdokoli. Nebo chcete poslat e-mail kolegovi, ale chcete aby uv∞°il, ╛e je od Vßs a ne od n∞jakΘho ╣pr²ma°e. Na v╣echno pot°ebujete kryptografii a v∞°te ╛e PGP je opravdu to pravΘ.

U╛ za dßvn²ch Φas∙ Julia Caesara se posφlaly tajnΘ dokumenty. StaΦilo zam∞nit pφsmena zprßvy za jinß nap°. takto: "A" bylo nahrazeno pφsmenem "E", "B" bylo nahrazeno pφsmenem "F", "C" bylo nahrazeno pφsmenem "G", atd., tak╛e se celß abeceda jakoby posunula o 4 znaky. Tak╛e ze zprßvy "Ahoj" se stalo "Eltn" a zprßva byla utajenß. Procesu, kter² z "Ahoj" ud∞lß "Eltn" se °φkß obecn∞ ╣ifrovßnφ (v anglick²ch textech encryption), procesu, kter² zprßvu roz╣ifruje se °φkß de╣iforvßnφ (decryption). P∙vodnφ zprßv∞ ("Ahoj") budeme °φkat hol² text (plaintext), za╣ifrovanΘ Φßsti ("Eltn") budeme °φkat za╣ifrovan² text (ciphertext).

Symetrickß kryptografie

To u╛ se blφ╛φme k pojmu "KonvenΦnφ" nebo "Symetrickß" kryptografie (Conventional cryptography), ve kterΘ vstupuje do hry tzv. klφΦ. KlφΦ spolu s hol²m textem vstupujφ do procesu ╣ifrovßnφ, jeho╛ v²stupem je za╣ifrovan² text. Pro roz╣ifrovßnφ zprßvy pot°ebujeme za╣ifrovan² text a op∞t klφΦ. V p°φkladu, kter² jsme si uvedli v²╣e si m∙╛eme p°edstavit, ╛e proces ╣ifrovßnφ bude "posunutφ pφsmene v abeced∞" a klφΦ bude Φφslo 4. KlφΦ m∙╛e b²t i v∞t╣φ. Nap°. 2|13|6, tj. Text "AHOJAHOJ" se bude ╣ifrovat takto :

A  H  O  |   J  A  H   |   O  J   =  C  U  T  L  N  M  R  W
2  13 5  |   2  13 5   |   2  13

Jako bychom rozsekali vstupnφ text na kousky po 3 pφsmenech (proto╛e dΘlka klφΦe je 3), ka╛d² kousek za╣ifrovali zvlß╣╗(prvnφ pφsmeno "posuneme" o 2 znaky, druhΘ o 13, t°etφ o 5) a za╣ifrovanΘ kousky zase spojili. Dekryptovßnφ probφhß velice podobn∞. Viz. obrßzek.

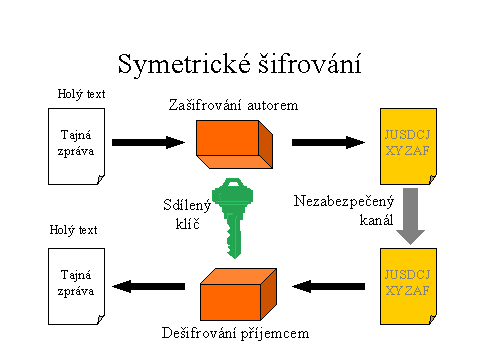
Tady bychom si m∞li pov╣imnout n∞kolika v∞cφ. Pokud je tajnost zprßvy zßvislß na utajenφ algoritmu ╣ifrovßnφ, je to V«DY ╣patn∞. Pokud by n∞kdo zjistil, jak ╛e to ╣ifruje Julius Caesar ("posouvß abecedu o 4 znaky"), mohl by Julius Caesar klidn∞ tenhle zp∙sob zahodit. SouΦasnΘ algoritmy ╣ifrovßnφ jsou obecn∞ znßmΘ a tajnost zprßvy zßvisφ pouze na tajnosti klφΦe.

Dal╣φ v∞c, kterΘ bychom si m∞li v╣imnout je dΘlka klφΦe. Zatφmco v prvnφm p°φpad∞ (klφΦ je 4, jeho dΘlka je tedy 1) se pφsmeno "A" za╣ifruje v╛dy stejn∞ (stane se z n∞ho "E"), v druhΘm p°φpad∞ to tak nenφ. Ve slov∞ "AHOJAHOJ" se prvnφ "AHOJ" za╣ifrovalo jako "CUTL", druhΘ "AHOJ" jako "NMRW".

Kryptoanal²za se zab²vß rozbφjenφm ╣ifer. Pokud p°ibli╛n∞ vφ, co hledß (zdrojov² k≤d programu v danΘm jazyce, text v angliΦtin∞, text ΦeskΘ pφsn∞), dokß╛e na zßklad∞ Φetnosti v²skytu jednotliv²ch pφsmen Φi slov a statistick²ch ·daj∙ pro dan² jazyky ╣ifru rozbφt (vylu╣tit). Znamenß to, ╛e pokud za╣ifrujete text "bflmpsvz", tak ani kryptoanal²za takov² text nerozlu╣tφ. Na druhou stranu je i Vßm takov²to text ·pln∞ k niΦemu. Tak╛e vlastnost, ╛e se stejnΘ Φßsti vstupnφho textu zak≤dujφ jinak, znesnadnφ kryptoanal²zu, co╛ chceme. Jinak °eΦeno, Φφm del╣φ klφΦ, tφm lep╣φ.

Nade╣el Φas si °φct, ╛e algoritmus "posouvßnφ pφsmen" se pro ╣ifrovßnφ rozhodn∞ nehodφ. ProΦ??? P°edstavme si nßsledujφcφ situaci. Alice a Bob spolu komunikujφ ╣ifrovan²m kanßlem (tj. zprßvy ╣ifrujφ klφΦem, kter² si p°edem vym∞nili a nikdo jin² ne╛ oni dva klφΦ neznß). Je ov╣em n∞kdo, Udo, kdo chce v∞d∞t, co si posφlajφ. Pro Uda toti╛ nemusφ b²t p°φli╣ obtφ╛nΘ zφskat n∞jakou zprßvu a jejφ zak≤dovanou podobu. Nap°. po╣le Bobovi zprßvu a chce ,aby ji Bob poslal Alici, ale aby zprßvu utajil. Pak poslouchß kanßl mezi Alicφ a Bobem a za╣ifrovanou zprßvu si odchytφ. Navφc znß algoritmus ╣ifrovßnφ (ten je obecn∞ znßm²). Na prvnφ pohled je vid∞t, ╛e pokud by Alice s Bobem pou╛φvali algoritmus "posouvßnφ pφsmen", Udo by ze znalosti p∙vodnφ zprßvy a za╣ifrovanΘ zprßvy jednodu╣e obdr╛el klφΦ.

Na╣t∞stφ existujφ jinΘ funkce, u kter²ch platφ, ╛e je v²poΦetnΘ velice obtφ╛nΘ zφskat klφΦ p°i znalosti p∙vodnφ zprßvy a za╣ifrovanΘ zprßvy (zßle╛φ na dΘlce klφΦe. P°i souΦasn²ch mo╛nostech nap°. 1000000000 let, co╛ je dost. DΘlka klφΦe 128 bit∙ (dnes asi 10 na t°icßtou devßtou let) staΦφ bohat∞ i pro daleko rychlej╣φ stroje ne╛ dne╣nφ) a zßrove≥ platφ, ╛e ╣ifrovßnφ a de╣ifrovßnφ (kdy╛ mßm klφΦ) je rychlΘ. Mezi tyhle algoritmy pat°φ DES, 3DES, CAST, IDEA, jejich╛ principy fungovßnφ se dozvφte ve v∞t╣in∞ knφ╛ek o kryprografii.

A nakonec v²hody a nev²hody symetrickΘ kryprografie, o kterΘ jsme se dote∩ bavili. V²hodou je jejφ rychlost. Dajφ se takΘ dob°e vyu╛φt pro ╣ifrovßnφ dat, kterß nikam nejdou (za╣ifruji svoje dokumenty na svΘm poΦφtaΦi, aby je nikdo nemohl Φφst). Nejv∞t╣φ nev²hodou je, ╛e pokud chceme s n∞k²m tajn∞ komunikovat, musφme si p°edem n∞jak²m bezpeΦn²m kanßlem p°edat klφΦ. To n∞kdy m∙╛e b²t obrovsk² problΘm. Druhß nev²hoda je poΦet klφΦ∙. P°edstavme si organizaci, v nφ╛ chce ka╛d² s ka╛d²m komunikovat tajn∞, tak aby nikdo t°etφ nemohl odposlouchßvat a tato organizace mß 10000 Φlen∙. Pak je pot°eba v celΘ organizaci mφt 5 milion∙ klφΦ∙. P°i existenci Internetu a 5 miliard lidφ na sv∞t∞ by bylo pot°eba 12 500 000 000 000 000 000 klφΦ∙.

Asymetrickß kryptografie

Existuje je╣t∞ dal╣φ zp∙sob kryptografie, a tφm je "Asymetrickß kryprografie" (Public key cryptography). Asymetrickß proto, ╛e vyu╛φvß jinΘho klφΦe pro ╣ifrovßnφ a jinΘho pro de╣ifrovßnφ (narozdφl od symetrickΘ). Viz nßsledujφcφ obrßzek.

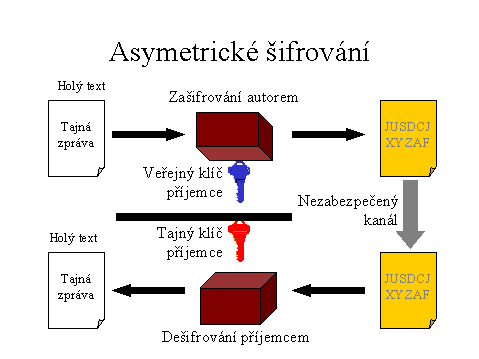
OznaΦenφ pro takovouto dvojici klφΦ∙ v anglickΘ literatu°e se naz²vß keypair - pßr klφΦ∙. KlφΦ, pomocφ kterΘho se ╣ifruje, se naz²vß ve°ejn² klφΦ (public key) a klφΦ, kter²m se de╣ifruje, se naz²vß soukrom² klφΦ (privßtnφ klφΦ, private key). Tahle definice sice nenφ ·pln∞ p°esnß, ale pozd∞ji bude up°esn∞na. Princip jak s tφmhle systΘmem pracovat, je nßsledujφcφ. Bob mß sv∙j pßr klφΦ∙. Jeden soukrom² a jeden ve°ejn². Jeho ve°ejn² klφΦ znajφ v╣ichni, soukrom² klφΦ znß jen Bob. Kdokoliv mu chce poslat tajnou zprßvu, za╣ifruje ji jeho ve°ejn²m klφΦem. Jedin², kdo tu zprßvu m∙╛e rozlu╣tit je Bob, dokonce ani odesφlatel ji neroz╣ifruje.

Tento princip mß svΘ v²hody. Hlavnφ v²hodou je to, ╛e lidΘ si nemusφ p°ed zahßjenφm vym∞nit klφΦe n∞jak²m neodposlouchßvan²m komunikaΦnφm kanßlem. Ve°ejn² klφΦ mohou znßt v╣ichni. Za druhΘ je pot°eba mΘn∞ klφΦ∙. Kdokoli chce posφlat tajnΘ v∞ci v∞ci Bobovi, pou╛ije Bob∙v ve°ejn² klφΦ.

Dal╣φ funkcφ, kterou je mo╛no realizovat pomocφ asymetrickΘ kryptografie, je tzv. digitßlnφ podpis. Co je to digitßlnφ podpis? Rozhodn∞ to nenφ podpis na konci e-mailu "Zdravφ T∞ Jirka, rosenmay@fi.muni.cz ". Ani to nenφ nßpis, ╛e autor tohohle Φlßnku je Ji°φ Rosenmayer. Cht∞li bychom to ud∞lat tak, aby podpis byl jednoznaΦn² (nikdo druh² ho nemohl ud∞lat) a aby se snadno poznalo, kdo zprßvu podepsal.

Jak tedy vypadß digitßlnφ podpis? Existujφ funkce (nap°. MD5), kter²m se °φkß ha╣ovacφ funkce. Ha╣ovacφ funkce d∞lajφ takzvan² otisk zprßvy (message digest). Ha╣ovacφ funkci dßme na vstup libovolnou zprßvu (libovoln∞ dlouhou) a na v²stupu obdr╛φme jejφ otisk, kter² mß pevnou dΘlku (128 nebo 160 bit∙). Pokud bychom ve zprßv∞ zm∞nili by╗ i jedinΘ pφsmenko, dostaneme na v²stupu ·pln∞ jin² otisk. Ha╣ovacφ funkce jsou znßmΘ a kdokoli si m∙╛e z jakΘkoliv zprßvy takov² otisk ud∞lat. Navφc platφ, ╛e je v²poΦetn∞ velice obtφ╛nΘ vytvo°it k libovolnΘ zprßv∞ jinou zprßvu, kterß mß stejn² otisk. (Asi tak stejn∞ obtφ╛nΘ jako roz╣ifrovat zprßvu bez klφΦe). Takov²to otisk se za╣ifruje soukrom²m klφΦem (pozor!!! soukrom²m, ne ve°ejn²m, jako u kryptovßnφ celΘ zprßvy) a dostaneme prßv∞ ╛ßdan² digitßlnφ podpis, kter² p°ipojφme na konec p∙vodnφ zprßvy.

Nap°. Alice podepφ╣e zprßvu sv²m soukrom²m klφΦem. Nikdo jin² ne╛ Alice takov² podpis nevytvo°φ, proto╛e jen Alice znß sv∙j soukrom² klφΦ. Samoz°ejm∞, n∞jak² ·toΦnφk m∙╛e zase podpis ze zprßvy umazat, ale nem∙╛e podvrhnout jinou zprßvu a podepsat ji jako Alice. Jak poznß Bob, ╛e zprßvu podepsala Alice? Roz╣ifruje podpis ve°ejn²m klφΦem Alice a dostane otisk. Zavolß ha╣ovacφ funkci (tu stejnou jako Alice - vstupem bude holß zprßva) a dostane prav² otisk tΘ zprßvy. Pak jej u╛ jen porovnß s otiskem, kter² si rozk≤doval ve°ejn²m klφΦem Alice, a pokud se rovnajφ, pak Bob vφ, ╛e zprßvu mohla podepsat jen Alice. Dokonkce ani Alice nem∙╛e tvrdit, ╛e to nenφ jejφ podpis a ╛e zprßvu nepodepsala.

ProΦ se vlastn∞ ╣ifruje otisk zprßvy a ne celß zprßva? Pokud by Alice za╣ifrovala celou zprßvu a p°ipojila ji na konec zprßvy p∙vodnφ, pak by zprßvu zdvojnßsobila, kde╛to p°ipojenφm otisku (samoz°ejm∞ za╣ifrovanΘho) se zprßva zv∞t╣φ jen o pßr byt∙.

Digitßlnφ podpis je aplikace, kterß se mo╛nß vyu╛φvß vφce, ne╛ samotnΘ ╣ifrovßnφ zprßv. Je to asi logickΘ, kdy╛ uvß╛φte, s kolika tajn²mi dokumenty a s kolika podepsan²mi dokumenty jste se v ╛ivot∞ setkali. Tak jako symetrickß, tak i asymetrickß kryptografie mß svΘ nev²hody. Za prvΘ je asi 1000x pomalej╣φ, ne╛ kryptografie symetrickß. Pozd∞ji se dozvφte, jak PGP vyu╛φvß v²hod obou zp∙sob∙.

Dal╣φ, p°φmo achilovou patou asymetrickΘ kryptografie, je pravost klφΦe. Musφte toti╛ 100% v∞d∞t, ╛e klφΦ pat°φ opravdu danΘ osob∞, tj. v∞d∞t ,╛e nenφ podvrhnut² (pokud Vßm ho dan² Φlov∞k osobn∞ nep°edal do ruky). Pokud jste do╣li a╛ sem a v╣echno chßpete, pak zbytek je hraΦka.

PGP se tvß°φ jako systΘm vyu╛φvajφcφ asymetrickou kryprografii a my jej tak zatφm m∙╛eme chßpat. Umo╛≥uje ╣ifrovat, podpisovat, roz╣ifrovat, ov∞°it podpis Va╣e zprßvy. Pokud jste Φetli pozorn∞ p°edchozφ pasß╛, budete pova╛ovat nßsledujφcφ ·daje za jasnΘ. Pokud budeme chtφt posφlat ╣ifrovanΘ zprßvy sv²m p°ßtel∙m (kte°φ taky musφ mφt PGP), pot°ebujeme k tomu nßsledujφcφ v∞ci: sv∙j pßr klφΦ∙, tj. soukrom² klφΦ (abyste mohli podepisovat vlastnφ zprßvy a de╣ifrovat zprßvy, co Vßm poslali ostatnφ) a ve°ejn² klφΦ (ten po╣leme sv²m p°ßtel∙m, aby mohli ov∞°ovat podpis a mohli ╣ifrovat zprßvy pro Vßs va╣im klφΦem ) a ve°ejnΘ klφΦe sv²ch p°ßtel (abyste mohli ╣ifrovat zprßvy, kterΘ posφlßte ostatnφm a ov∞°ovat jejich podpisy).

Vidφme, ╛e pot°ebujeme celou klφΦenku, p°esn∞ji krou╛ek s klφΦi. P°esn∞ tak se toti╛ v PGP naz²vß soubor, ve kterΘm jsou uchovßny ve°ejnΘ klφΦe - KEYRING - krou╛ek klφΦ∙. V PGP jsou dva takovΘto soubory. Soubor s ve°ejn²mi klφΦi a soubor se soukrom²mi klφΦi. M∙╛ete mφt i vφce sv²ch pßr∙ klφΦ∙. Ka╛d² m∙╛ete pou╛φvat pro jinΘ p°φle╛itosti. Jin² pou╛φvat pro komunikaci s p°ßteli, jin² (t°eba siln∞j╣φ) pro utajovßnφ dokument∙. StaΦφ snad je╣t∞ dodat, ╛e v PGP je vß╣ soukrom² klφΦ navφc chrßn∞n heslem (passphrase - heslo, ale m∞lo by b²t del╣φ, nejlΘpe n∞kolik slov. Nap°. "Maminka m∞ nemß rßda"), pro p°φpad, ╛e by Vß╣ klφΦ n∞kdo zφskal z Va╣eho poΦφtaΦe (proto musφte po°ßd heslo zadßvat p°i roz╣ifrovßnφ a podepisovßnφ). Tyhle informace by mohly staΦit na to abyste PGP mohli pou╛φvat.