[Top] [Contents] [Index] [ ? ]

Enigma

ⁿ╘╧ ╥╒╦╧╫╧─╙╘╫╧ ╧╨╔╙┘╫┴┼╘ ╦┴╦ ╒╙╘┴╬╧╫╔╘╪ ╔ ╔╟╥┴╘╪ ╫ Enigma. ∩╬╧ ╙╧╧╘╫┼╘╙╘╫╒┼╘ ╫┼╥╙╔╔ Enigma ╨╧─ ╬╧═┼╥╧═ 1.00.

Copyright © 2003, 2004, 2005, 2006 Daniel Heck ╔ ─╥╒╟╔┼ ╒▐┴╙╘╬╔╦╔

δ╧╨╔╥╧╫┴╬╔┼ ╔ ╥┴╙╨╥╧╙╘╥┴╬┼╬╔┼ ▄╘╧╟╧ ╞┴╩╠┴ ╙ ╔┌═┼╬┼╬╔╤═╔ ╔╠╔ ┬┼┌ ╥┴┌╥┼█┼╬╧ ╠└┬┘═ ╙╨╧╙╧┬╧═ ┬┼┌ ╧╘▐╔╙╠┼╬╔╩, ┼╙╠╔ ╙╧╚╥┴╬┼╬┘ ╒╫┼─╧═╠┼╬╔┼ ╧┬ ┴╫╘╧╥╙╦╔╚ ╨╥┴╫┴╚ ╔ ▄╘╧ ╒╫┼─╧═╠┼╬╔┼.

1. ≈╫┼─┼╬╔┼   ·╬┴╦╧═╙╘╫╧ ╙ Enigma
2. Θ╟╥┴   δ┴╦ ╔╟╥┴╘╪ ╫ Enigma
3. ε┼╦╧╘╧╥┘┼ ╔╟╥╧╫┘┼ ╧┬▀┼╦╘┘  ∩╨╔╙┴╬╔┼ ╬┼╦╧╘╧╥┘╚ ╔╟╥╧╫┘╚ ╧┬▀┼╦╘╧╫
4. Σ╧╨╧╠╬╔╘┼╠╪╬┘┼ ╘┼═┘  Σ╧╨╧╠╬╔╘┼╠╪╬┘┼ ╫╧┌═╧╓╬╧╙╘╔ ╔ ┴─═╔╬╔╙╘╥╔╥╧╫┴╬╔┼
5. ≤╨╧╩╠┼╥┘  ≡╧─╙╦┴┌╦╔ ─╠╤ ╬┼╦╧╘╧╥┘╚ ╙╠╧╓╬┘╚ ╒╥╧╫╬┼╩
6. Γ╠┴╟╧─┴╥╬╧╙╘╔  ≤╧┌─┴╘┼╠╔ ╔ ┬╠┴╟╧─┴╥╬╧╙╘╔









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 1. ≈╫┼─┼╬╔┼ 





1.1 ∩┬ Enigma  ε┼╦╧╘╧╥┘┼ ╞┴╦╘┘ ╧┬ Enigma


1.2 ⌡╙╘┴╬╧╫╦┴                  ≡╧╠╒▐┼╬╔┼ ╔ ╒╙╘┴╬╧╫╦┴ Enigma



1.3 ≥┴╙╨╥╧╙╘╥┴╬┼╬╔┼ Enigma           ≡┼╥┼─┴╫┴╩╘┼ ╦╧╨╔╔ ╫┴█╔═ ─╥╒┌╪╤═!













[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 1.1 ∩┬ Enigma 



≤╦┴┌┴╘╪, ▐╘╧ Enigma ? ╔╟╥┴-╟╧╠╧╫╧╠╧═╦┴ ▄╘╧ ╨╥┼╒═┼╬╪█┼╬╔┼. ε┴ ╙┴═╧═ ─┼╠┼ Enigma 
▄╘╧ ╧╟╥╧═╬┴╤ ╦╧╠╠┼╦├╔╤ ╟╧╠╧╫╧╠╧═╧╦, ╔ ╦┴╓─┘╩ ╔┌ ┼┼ 550 ╒╬╔╦┴╠╪╬┘╚ ╒╥╧╫╬┼╩ ╙╬╧╫┴ 
╔ ╙╬╧╫┴ ╨╧╘╥┼┬╒┼╘ ╙╧╧┬╥┴┌╔╘┼╠╪╬╧╙╘╔, ╠╧╫╦╧╙╘╔ ╔ ╨╧─╠╔╬╬╧╩ ╙╔╠┘ ╫╧╠╔ ╧╘ ╙╫╧╔╚ ╔╟╥╧╦╧╫. 
Enigma ╨╥╧╙╘┴ ╫ ╔┌╒▐┼╬╔╔, ╔╬╘┼╥┼╙╬┴ ╫ ╔╟╥┼ ╔ ╙╠╧╓╬┴ ╫ ╧╫╠┴─┼╬╔╔. ∩╬┴ ═╧╓┼╘ ╥┴┌╫╠┼▐╪ 
╨╧╠╪┌╧╫┴╘┼╠┼╩ ╨╧▐╘╔ ╠└┬╧╟╧ ╫╧┌╥┴╙╘┴. ∩╬┴ ╙╧─┼╥╓╔╘ ╙╧╘╬╔ ╒╥╧╫╬┼╩. Θ, ┼╙╠╔ ▄╘╧╟╧ 
╬┼ ─╧╙╘┴╘╧▐╬╧, ╧╬┴ ╘┴╦╓┼ ╨╧╠╬╧╙╘╪└ ┬┼╙╨╠┴╘╬┴. σ╙╠╔ ≈┴═ ╬╥┴╫╤╘╙╤ ╔╟╥┘-╟╧╠╧╫╧╠╧═╦╔ 
╔ ╒ ≈┴╙ ╘╫┼╥─┴╤ ╥╒╦┴, Enigma ╫╧┌═╧╓╬╧ ┌┴╩═┼╘ ≈┴╙ ╬┴ ╨╥╧╘╤╓┼╬╔╔ ├┼╠┘╚ ▐┴╙╧╫.



π┼╠╪ ╔╟╥┘ ? ╬┴╩╘╔ ╔ ╧╘╦╥┘╘╪ ╨┴╥┘ `Oxyd'-╦┴═╬┼╩ ╧─╔╬┴╦╧╫╧╟╧ ├╫┼╘┴. ≡╥╧╙╘╧? Σ┴. 
∞┼╟╦╧? δ╧╬┼▐╬╧, ╬┼╘! ≤╦╥┘╘┘┼ ╠╧╫╒█╦╔, ╧╟╥╧═╬┘┼ ╠┴┬╔╥╔╬╘┘, ╠┴┌┼╥╬┘┼ ╠╒▐╔ ╔, ╙┴═╧┼ 
╟╠┴╫╬╧┼, ┬┼╙▐╔╙╠┼╬╬┘┼ ╨╥╔▐╒─╠╔╫┘┼ ╟╧╠╧╫╧╠╧═╦╔ ╧┬┘▐╬╧ ╨┼╥┼╦╥┘╫┴└▌╔┼ ≈┴═ ╨╥╤═╧╩ ╨╒╘╪ 
╦ Oxyd-╦┴═╬╤═. Θ╟╥╧╫┘┼ ╧┬▀┼╦╘┘ Enigma (╔╚ ┌─┼╙╪ ╙╧╘╬╔, ▐╘╧┬┘ ≈┘ ╬┼ ╙╦╒▐┴╠╔) 
╫┌┴╔═╧─┼╩╙╘╫╒└╘ ═╬╧╟╧▐╔╙╠┼╬╬┘═╔ ╬┼╨╥┼─╙╦┴┌╒┼═┘═╔ ╙╨╧╙╧┬┴═╔, ╔ ╨╧╙╦╧╠╪╦╒ ═╬╧╟╔┼ ╔┌ 
╬╔╚ ╨╧─▐╔╬╤└╘╙╤ ┌┴╦╧╬┴═ ╞╔┌╔╦╔ (┴ ╘╧▐╬┼┼, ╧╙╧┬┘═ ┌┴╦╧╬┴═ ╞╔┌╔╦╔ Enigma), ╒╨╥┴╫╠┼╬╔┼ 
╔═╔ ╙ ╨╧═╧▌╪└ ═┘█╔ ╬┼ ╫╙┼╟─┴ ╘╥╔╫╔┴╠╪╬╧ ....



≡┼╥╫╧╬┴▐┴╠╪╬┴╤ ├┼╠╪ ╨╥╧┼╦╘┴ Enigma ┬┘╠┴ ╙╧╚╥┴╬╔╘╪ ─╒╚ ╙┼╥╔╔ ╔╟╥ Oxyd, ╨╧╙╠┼ ╘╧╟╧ 
╦┴╦ ╔╚ ╔┌─┴╘┼╠╪ ╥┼█╔╠ ╨╧╦╔╬╒╘╪ ╔╟╥╧╫╧╩ ┬╔┌╬┼╙ ╫ 2002 ╟╧─╒. ⌡ ╨╧╦╠╧╬╬╔╦╧╫ ▄╘╧╩ 
┌╬┴═┼╬╔╘╧╩ ╔╟╥┘ ┬╒─┼╘ ▐╒╫╙╘╫╧ ─┼╓┴ ╫└. ε╧ ╙╨╒╙╘╤ ╟╧─┘, Enigma ╫╨╔╘┴╠┴ ╔─┼╔ ╔┌ 
═╬╧╓┼╙╘╫┴ ─╥╒╟╔╚ ╨╧╨╒╠╤╥╬┘╚ ╔╟╥ ╔ ─╧┬┴╫╔╠┴ ╙╫╧╔ ╒╬╔╦┴╠╪╬┘┼ ╧╙╧┬┼╬╬╧╙╘╔ ╦ ╦┴╓─╧╩ 
╔┌ ╬╔╚.



Enigma ─╧╙╘╒╨╬┴ ─╠╤ Windows, Mac OS X, ╔ ┬╧╠╪█╔╬╙╘╫┴ ╥┴┌╬╧╫╔─╬╧╙╘┼╩ Linux ╔ ─╥╒╟╔╚ 
╙╧╫╥┼═┼╬╬┘╚ Unix'╧╫. ∩╬┴ ╨┼╥┼╫┼─┼╬┴ ╬┴ ═╬╧╟╔┼ ╤┌┘╦╔. Σ┴╓┼ ▄╘╧ ╥╒╦╧╫╧─╙╘╫╧ ─╧╙╘╒╨╬╧ 
╬┴ ╬┼╙╦╧╠╪╦╔╚ ╤┌┘╦┴╚.



≤╒▌┼╙╘╫╒┼╘ ╧╞╔├╔┴╠╪╬┴╤ ─╧═┴█╬╤╤ ╙╘╥┴╬╔├┴ Enigma, 
╦╧╘╧╥┴╤ ╙╧─┼╥╓╔╘ ╙╘╥┴╬╔├┘ ╙╦╥╔╬█╧╘╧╫, ┌┴╟╥╒┌╧╦, ╨╧╙╠┼─╬╔╚ ╬╧╫╧╙╘┼╩ ╔ ╙┴═╒└ ╨╧╙╠┼─╬└└ 
╫┼╥╙╔└ ▄╘╧╟╧ ╥╒╦╧╫╧─╙╘╫┴.
≤ ╥┴┌╥┴┬╧╘▐╔╦┴═╔ Enigma ╫╙┼╟─┴ ═╧╓╬╧ ╙╫╤┌┴╘╪╙╤ ╙ ╨╧═╧▌╪└ ▄╠┼╦╘╥╧╬╬╧╩ ╨╧▐╘┘ ╨╧ ┴─╥┼╙╒
enigma-devel@nongnu.org.



Enigma ▄╘╧ ╙╫╧┬╧─╬╧┼ ╨╥╧╟╥┴══╬╧┼ ╧┬┼╙╨┼▐┼╬╔┼, ─╥╒╟╔═╔ ╙╠╧╫┴═╔, ╨╥╔╫┼╘╙╘╫╒┼╘╙╤ 
╦╧╨╔╥╧╫┴╘╪ ┼┼ ╔ ─┴╫┴╘╪ ┼┼ ≈┴█╔═ ─╥╒┌╪╤═ (╙═╧╘╥╔╘┼ (see section ≥┴╙╨╥╧╙╘╥┴╬┼╬╔┼ Enigma).  
Enigma ╥┴┌╥┴┬┴╘┘╫┴┼╘╙╤ ═┴╠┼╬╪╦╧╩ ╟╥╒╨╨╧╩ ─╧┬╥╧╫╧╠╪├┼╫, ╫╙┼ ╔┌ ╬┴╙ ╥┴┬╧╘┴└╘ ╫ ╬┴█┼ 
╙╫╧┬╧─╬╧┼ ╫╥┼═╤. σ╙╠╔ ≈┴═ ╨╧╬╥┴╫╔╠┴╙╪ ╔╟╥┴, ╨╧╓┴╠╒╩╙╘┴ ╨╥╔█╠╔╘┼ ╬┴═ ▄╠┼╦╘╥╧╬╬╧┼ ╨╔╙╪═╧. 
ⁿ╘╧ ╨╧╓┴╠╒╩ ┼─╔╬╙╘╫┼╬╬┴╤ ╫┼▌╪, ╦╧╘╧╥┴╤ ╫╙┼╟─┴ ╨╥╔╫╧─╔╘ ╦ ╘╧═╒, ▐╘╧ ═┘ ╨╧╙╫╤▌┴┼═ ▄╘╧╩ 
╔╟╥┼ ┬┼╙▐╔╙╠┼╬╬╧┼ ═╬╧╓┼╙╘╫╧ ▐┴╙╧╫.










[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 1.2 ⌡╙╘┴╬╧╫╦┴ 



≡╧╙╠┼─╬╤╤ ╫┼╥╙╔╤ Enigma ═╧╓┼╘ ┬┘╘╪ ┌┴╟╥╒╓┼╬┴ ╙╧
╙╘╥┴╬╔├┘ ┌┴╟╥╒┌╧╦ Enigma. ⁿ╘┴ 
╙╘╥┴╬╔├┴ ╙╧─┼╥╓╔╘ ╨┴╦┼╘┘ ─╠╤ ╙╠┼─╒└▌╔╚ ╧╨┼╥┴├╔╧╬╬┘╚ ╙╔╙╘┼═:





 Windows


≈┼╥╙╔╤ Enigma ─╠╤ Windows ╥┴╙╨╥╧╙╘╥┴╬╤┼╘╙╤, ╦┴╦ ╙┴═╧╥┴╙╨┴╦╧╫┘╫┴└▌┴╤╙╤ ╨╥╧╟╥┴══┴. 
≡╥╧╙╘╧ ╙╦┴▐┴╩╘┼ ╔ ┌┴╨╒╙╘╔╘┼ ╨╥┼─╠╧╓┼╬╬┘╩ ╞┴╩╠ `.exe'.





 Unix


≤╒▌┼╙╘╫╒└╘ ┬╔╬┴╥╬┘┼ ╨┴╦┼╘┘ ─╠╤ ╬┼╦╧╘╧╥┘╚ ╨╧╨╒╠╤╥╬┘╚ ─╔╙╘╥╔┬╒╘╔╫╧╫ Linux, ╘┴╦╔╚ ╦┴╦ 
SUSE, Redhat ╔╠╔ Debian. Σ╠╤ ─╥╒╟╔╚ Unix-╨╧─╧┬╬┘╚ ╧╨┼╥┴├╔╧╬╬┘╚ ╙╔╙╘┼═ ╧┬┘▐╬╧ ╙┴═╧┼ 
╨╥╧╙╘╧┼ ╥┼█┼╬╔┼ ▄╘╧ ╙┬╧╥╦┴ Enigma ╔┌ ╔╙╚╧─╬┘╚ ╦╧─╧╫.





 Mac OS X


Σ╠╤ ╧╨┼╥┴├╔╧╬╬╧╩ ╙╔╙╘┼═┘ ╫┼╥╙╔╔ X ╒╙╘┴╬╧╫╦┴ ╬┼ ╘╥┼┬╒┼╘╙╤, ╨╥╧╙╘╧ ┌┴╨╒╙╘╔╘┼ ╞┴╩╠
`.dmg' ╔╠╔ `.tar.gz'.








≤╘╥┴╬╔├┴ ┌┴╟╥╒┌╧╦, ╦┴╦ ╨╥┴╫╔╠╧, ╙╧─┼╥╓╔╘ ┬╧╠┼┼ ╨╧─╥╧┬╬╒└ ╔ ╙╧╫╥┼═┼╬╬╒└ ╔╬╞╧╥═┴├╔└. 
σ╙╠╔ ≈┘ ╬┼ ═╧╓┼╘┼ ┌┴╙╘┴╫╔╘╪ Enigma ╥┴┬╧╘┴╘╪ ╬┴ ≈┴█┼═ ╦╧═╨╪└╘┼╥┼, ╬┼ ┬╧╩╘┼╙╪ ╨╧╨╥╧╙╔╘╪ 
╨╧═╧▌╔ ╫ ╥┴╙╙┘╠╦┼ Enigma
(enigma-devel@nongnu.org).









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 1.3 ≥┴╙╨╥╧╙╘╥┴╬┼╬╔┼ Enigma 



Enigma ▄╘╧ ╙╫╧┬╧─╬╧┼ ╨╥╧╟╥┴══╬╧┼ ╧┬┼╙╨┼▐┼╬╔┼ ╔ ╧╬┴ ═╧╓┼╘ ╥┴╙╨╥╧╙╘╥┴╬╤╘╪╙╤ ╬┴ ╒╙╠╧╫╔╤╚ 
GNU General Public License (GPL). ⁿ╘┴ ╠╔├┼╬┌╔╤ ╨╧╙╘┴╫╠╤┼╘╙╤ ╙ ╦┴╓─┘═ ╔┌─┴╬╔┼═ Enigma 
(╔╠╔ ╫ ╞┴╩╠┼ `COPYING' ╔╠╔ ╫ ╞┴╩╠┼
`COPYING.txt').  σ╙╠╔ ≈┘ ╚╧╘╔╘┼ ╘╧╠╪╦╧ ╔╟╥┴╘╪ ╫ Enigma, ≈┴═ ╬┼ ╧┬╤┌┴╘┼╠╪╬╧ 
▐╔╘┴╘╪ ╫╙┼ ╘┼ ╘┼╥═╔╬┘ (╙╦╧╥┼┼ ╫╙┼╟╧ ≈┘ ╔ ╬┼ ┌┴╚╧╘╔╘┼). Σ╠╤ ≈┴╙, ╠╔├┼╬┌╔╤ ╫ ╧╙╬╧╫╬╧═ 
╟╠┴╙╔╘: Θ╟╥┴╩╘┼ ╫ Enigma ╙╦╧╠╪╦╧ ╚╧╘╔╘┼, ╨╧╦┴ ╚╧╘╔╘┼ ╔ ═╧╓┼╘┼ ─┴╫┴╘╪ ┼┼ ╙╫╧╔═ ─╥╒┌╪╤═!



σ╙╠╔ ≈┘ ╚╧╘╔╘┼ ╔┌═┼╬╔╘╪ Enigma ╔╠╔ ╙╨╧╙╧┬╙╘╫╧╫┴╘╪ ┼┼ ─┴╠╪╬┼╩█┼╩ ╥┴┌╥┴┬╧╘╦┼, ╨╧╓┴╠╒╩╙╘┴ 
╨╥╧▐╘╔╘┼ ╔├┼╬┌╔└, ╫╙┼╟╧ ╧─╔╬ ╥┴┌ ╫ ╓╔┌╬╔. ∞╔├┼╬┌╔╤ GPL ╟┴╥┴╬╘╔╥╒┼╘, ▐╘╧ Enigma 
┬╒─┼╘ ╧╙╘┴╫┴╘╪╙╤ ╙╫╧┬╧─╬┘═ ╨╥╧╟╥┴══╬┘═ ╧┬┼╙╨┼▐┼╬╔┼═ ╫ ┬╒─╒▌┼═. ≈ ▐┴╙╘╬╧╙╘╔, ┼╙╠╔ 
≈┘ ╔┌═┼╬╤┼╘┼ Enigma ╔╠╔ ╥┴╙╨╥╧╙╘╥┴╬╤┼╘┼ ╔┌═┼╬┼╬╬╒└ ╫┼╥╙╔└, ≈┘ ╬┼ ═╧╓┼╘┼ ╧╘╬╤╘╪ ╬╔ 
╒ ╦╧╟╧ ─╥╒╟╧╟╧ ╨╥┴╫╧ ╔╙╨╧╠╪┌╧╫┴╘╪, ╔┌═┼╬╤╘╪ ╔ ╥┴╙╨╥╧╙╘╥┴╬╤╘╪ Enigma ╔╠╔ ╨╥╧╔┌╫╧─╬┘┼ 
╧╘ ╬┼┼.



≡╥┼─┘─╒▌╔┼ ─╫┴ ┴┬┌┴├┴ ╬┼ ┌┴═┼╬╤└╘ ╬┴╙╘╧╤▌╒└ ╠╔├┼╬┌╔└, ╬╧ ─┴└╘ ╨╥┼─╙╘┴╫╠┼╬╔┼ ╧ ╬┼╩ 
╫ ╧┬▌╔╚ ▐┼╥╘┴╚ ╬┴ ╨╥╧╙╘╧═ ╥╒╙╙╦╧═. ≡╧╓┴╠╒╩╙╘┴ ╧┬╥┴╘╔╘┼╙╪ ╦ GPL, ┼╙╠╔ ≈┘ ╬┼ ╧╨╥┼─┼╠╔╠╔╙╪ 
╔╠╔ ┼╙╠╔ ≈┴═ ╬╒╓╬╧ ┌╬┴╘╪ ┬╧╠╪█┼ ╨╧─╥╧┬╬╧╙╘┼╩.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2. Θ╟╥┴ 





2.1 ·╬┴╦╧═╙╘╫╧  ≡┼╥┼─╫╔╓┼╬╔┼ ╨╧ ═┼╬└ ╔ ╬┴▐┴╠╧ ╔╟╥┘


2.2 ≡╥┴╫╔╠┴ Θ╟╥┘             δ┴╦ ╔╟╥┴╘╪ ╫ Enigma



2.3 ⌡╨╥┴╫╠┼╬╔┼  δ╧═┴╬─┘ ╦╠┴╫╔┴╘╒╥┘ ╔ ═┘█╔












[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2.1 ·╬┴╦╧═╙╘╫╧ 



≡╧╙╠┼ ┌┴╨╒╙╦┴ Enigma, ≈┘ ╧╦┴╓┼╘┼╙╪ ╫ ╟╠┴╫╬╧═ ═┼╬└, ╧╘╦╒─┴ ≈┘ ═╧╓┼╘┼ ╬┴▐┴╘╪ ╬╧╫╒└ 
╔╟╥╒, ╒╙╘┴╬╧╫╔╘╪ ╬┼╦╧╘╧╥┘┼ ╨┴╥┴═┼╘╥┘ ╔╠╔ ╫┘╩╘╔ ╔┌ ╔╟╥┘, ┼╙╠╔ ≈┴═ ╬┴─╧┼╠╧. ≤╠┼─╒└▌╔┼ 
╥┴┌─┼╠┘ ╨╧┌╬┴╦╧═╤╘ ≈┴╙ ╙ ═┼╬└ ╒╥╧╫╬┼╩ ╔ ═┼╬└ ╬┴╙╘╥╧┼╦; ╫╙┼ ╧╙╘┴╠╪╬╧┼ ═╧╓╬╧ ╬┴─┼╤╘╙╤ 
╟╧╫╧╥╔╘ ╙┴═╧ ┌┴ ╙┼┬╤. φ╬╧╟╔┼ ═┼╬└ ╨╥┼─╧╙╘┴╫╠╤└╘ ╔╬╘┼╥┴╦╘╔╫╬╒└ ╨╧═╧▌╪; ╨╥╧╙╘╧ ╬┴╓═╔╘┼ 
╦╠┴╫╔█╒
F1.





2.1.1 φ┼╬└ ╒╥╧╫╬┼╩  ≈┘┬╔╥┴┼╘ ╙╠┼─╒└▌╔╩ ╒╥╧╫┼╬╪


2.1.2 φ┼╬└ ≡┴╦┼╘ ╒╥╧╫╬┼╩  ≈┘┬╔╥┴┼╘ ╨┴╦┼╘ ╒╥╧╫╬┼╩


2.1.3 ε┴╙╘╥╧╩╦╔                  ≡╥╔╙╨╧╙╧┬╪╘┼ Enigma ╨╧─ ╙╫╧╔ ╨╥┼─╨╧▐╘┼╬╔╤



2.1.4 Θ╬╙╨┼╦╘╧╥ ╒╥╧╫╬╤  ≡╧─╥╧┬╬┴╤ ╔╬╞╧╥═┴├╔╤ ╧┬ ╒╥╧╫╬┼












[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2.1.1 φ┼╬└ ╒╥╧╫╬┼╩ 



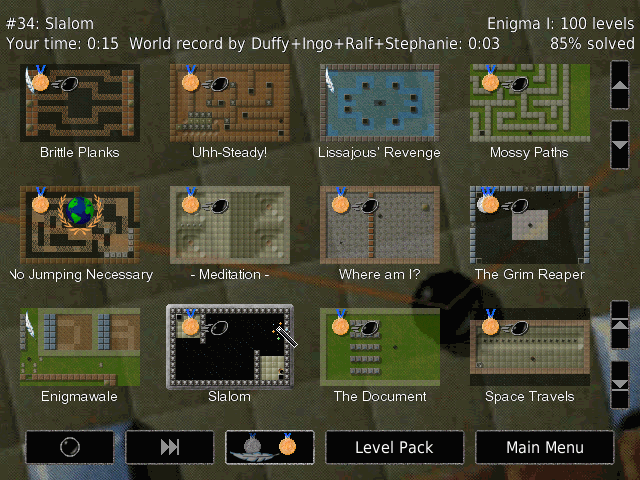
ε┴╓┴╘╔┼ ╬┴ "ε┴▐┴╘╪ ╔╟╥╒" ╫ ╟╠┴╫╬╧═ ═┼╬└ ╨╥╔╫┼─┼╘ ≈┴╙ ╦ ═┼╬└ ╒╥╧╫╬┼╩, ╦╧╘╧╥╧┼ 
╫┘╟╠╤─╔╘ ╨╥╔┬╠╔┌╔╘┼╠╪╬╧ ╦┴╦ ▄╘╧:



images/levelmenu



ⁿ╦╥┴╬ ╙╧╙╘╧╔╘ ╔┌ ╘╥┼╚ ╧┬╠┴╙╘┼╩: ╫┼╥╚╬╤╤ ╧┬╠┴╙╘╪ ╙╧─┼╥╓╔╘ ╔╬╞╧╥═┴├╔└ ╧ ╫┘┬╥┴╬╬╧═ 
╫ ─┴╬╬┘╩ ═╧═┼╬╘ ╒╥╧╫╬┼ ╔ ╘┼╦╒▌┼═ ╨┴╦┼╘┼ ╒╥╧╫╬┼╩, ╙╥┼─╬╤╤ ╧┬╠┴╙╘╪ ╨╧╦┴┌┘╫┴┼╘ ╫╔─ 
─╧╙╘╒╨╬┘╚ ╒╥╧╫╬┼╩, ┴ ╫╬╔┌╒ ╬┴╚╧─╔╘╙╤ ╥╤─ ╦╬╧╨╧╦.



≈┘ ═╧╓┼╘┼ ╨┼╥┼─╫╔╟┴╘╪╙╤ ╨╧ ╙╨╔╙╦╒ ╒╥╧╫╬┼╩ ╔╠╔ ╔╙╨╧╠╪┌╒╤ ═┴╠┼╬╪╦╔┼ ╦╬╧╨╦╔ ╙╧ 
╙╘╥┼╠╦┴═╔ ╙╨╥┴╫┴, ╔╠╔ ╨╧╠╪┌╒╤╙╪ ╦╠┴╫╔█┴═╔ ╙╧ ╙╘╥┼╠╦┴═╔. Σ╠╤ ╬┴▐┴╠┴ ╬╧╫╧╩ ╔╟╥┘ 
╨╥╧╙╘╧ ╦╠╔╦╬╔╘┼ ╬┴ ╔┌╧┬╥┴╓┼╬╔╔ ═┼╙╘╬╧╙╘╔ ╬┴ ╦╧╘╧╥╧╩ ≈┘ ╚╧╘╔╘┼ ╔╟╥┴╘╪ ╔╠╔ ╬┴╓═╔╘┼
Enter.



≈ Enigma ┼╙╘╪ ─╫┴ ╒╥╧╫╬╤ ╙╠╧╓╬╧╙╘╔: "╨╥╧╙╘╧╩" ╔ "╬╧╥═┴╠╪╬┘╩". ■╘╧┬┘ ╨┼╥┼╦╠└▐╔╘╪╙╤ 
═┼╓─╒ ╨╥╧╙╘╧╩ ╔ ╬╧╥═┴╠╪╬╧╩ ╙╠╧╓╬╧╙╘╪└, ╬┴╓═╔╘┼ ╦╬╧╨╦╒ ╫ ├┼╬╘╥┼ ╥╤─┴ ╦╬╧╨╧╦: 
╨┼╥┼╦╠└▐╔╘┼╙╪ ╬┴ ┌╬┴▐╧╦ ╙ ╔┌╧┬╥┴╓┼╬╔┼═ ╙┼╥┼┬╥╤╬╬╧╩ ═┼─┴╠╔ ╔ ╨┼╥┴, ┼╙╠╔ ≈┘ ╨╥┼─╨╧▐╔╘┴┼╘┼ 
╒╥╧╫╬╔ ╨╧╠┼╟▐┼ ╔╠╔ ╙ ╔┌╧┬╥┴╓┼╬╔┼═ ┌╧╠╧╘╧╩ ═┼─┴╠╔ ─╠╤ ╬╧╥═┴╠╪╬╧╟╧, ┬╧╠┼┼ ╙╠╧╓╬╧╟╧, 
╥┼╓╔═┴ ╔╟╥┘.



≈ ╒╨╥╧▌┼╬╬╧╩ ╫┼╥╙╔╔ ─╧╙╘╒╨╬┘ ╬┼ ╫╙┼ ╒╥╧╫╬╔; ╨╧▄╘╧═╒ ╧╬╔ ╧┬╧┌╬┴▐┼╬┘ ╨┼╥╧═ (┼╙╠╔ 
≈┘ ┼▌┼ ╔╚ ╬┼ ╥┼█╔╠╔) ╔╠╔ ╙┼╥┼┬╥╤╬╬╧╩ ═┼─┴╠╪└ ╫ ╫┼╥╚╬┼═ ╠┼╫╧═ ╒╟╠╒ ╔╚ ╔┌╧┬╥┴╓┼╬╔╤.



≈┘ ═╧╓┼╘┼ ╨┼╥┼╩╘╔ ╬┴ ╙╠┼─╒└▌╔╩ ╒╥╧╫┼╬╪ ╬┴╓┴╫ ╔╠╔ F5, ╔╠╔ ╦╬╧╨╦╒
>>| ╫ ╬╔╓╬┼═ ╥╤─╒. ·╬┴▐┼╬╔┼ ╙╠╧╫┴ "╙╠┼─╒└▌╔╩" ╫ ╨╥┼─┘─╒▌┼═ ╨╥┼─╠╧╓┼╬╔╔ 
┌┴╫╔╙╔╘ ╧╘ ╥┼╓╔═┴, ╦╧╘╧╥┘╩ ≈┘ ╫┘┬╥┴╠╔ ╙┴═╧╩ ╠┼╫╧╩ ╦╬╧╨╦╧╩ ╫ ╬╔╓╬┼═ ╥╤─╒.





⌡╥╧╫┼╬╪ ═╧╓┼╘ ─╧╨╧╠╬╔╘┼╠╪╬╧ ╧┬╧┌╬┴▐┴╘╪╙╤ ═┴╠┼╬╪╦╔═ ╦╥┴╙╬┘═ ╘╥┼╒╟╧╠╪╬╔╦╧═ ╙ 
╫╧╙╦╠╔├┴╘┼╠╪╬┘═ ┌╬┴╦╧═ ╫ ╫┼╥╚╬┼═ ╠┼╫╧═ ╒╟╠╒. ⁿ╘╧╘ ┌╬┴╦ ╒╫┼─╧═╔╘ ≈┴╙, ┼╙╠╔ ╒╥╧╫┼╬╪ 
┬┘╠ ╧┬╬╧╫╠┼╬ ╨╧╙╠┼ ╘╧╟╧ ╦┴╦ ≈┘ ┼╟╧ ╥┼█╔╠╔. ≈┘ ╙═╧╓┼╘┼ ╒╫╔─┼╘╪ ┼╟╧ ╘╧╠╪╦╧, ┼╙╠╔ 
≈┘ ╧┬╬╧╫╔╘┼ Enigma ─╧ ┬╧╠┼┼ ╬╧╫╧╩ ╫┼╥╙╔╔.



≈┘ ═╧╓┼╘┼ ╨┼╥┼═┼▌┴╘╪╙╤ ╨╧ ═┼╬└ ╒╥╧╫╬┼╩ ╙ ╨╧═╧▌╪└ ╙╠┼─╒└▌╔╚ ╦╠┴╫╔█:





 ESC


≈┼╥╬╒╘╪╙╤ ╦ ╨╥┼─┘─╒▌┼═╒ ═┼╬└





 F1


≡╧╦┴┌┴╘╪ ╨╧═╧▌╪





 F5


≡┼╥┼╩╘╔ ╦ ╙╠┼─╒└▌┼═╒ ╒╥╧╫╬└, ┴╬┴╠╧╟╔▐╬╧ ╦╬╧╨╦┼ >>| 





 ≤╘╥┼╠╦╔


≤═┼╬╔╘╪ ╒╥╧╫┼╬╪





 Enter


Θ╟╥┴╘╪ ╬┴ ╫┘┬╥┴╬╬╧═ ╒╥╧╫╬┼





 ≡╥╧┬┼╠


≡┼╥┼╩╘╔ ╦ ╙╠┼─╒└▌┼═╒ ╨┴╦┼╘╒ ╒╥╧╫╬┼╩





 Backspace


≡┼╥┼╩╘╔ ╦ ╨╥┼─┘─╒▌┼═╒ ╨┴╦┼╘╒ ╒╥╧╫╬┼╩














[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2.1.2 φ┼╬└ ≡┴╦┼╘ ╒╥╧╫╬┼╩ 



≤ Enigma ╨╧╙╘┴╫╠╤┼╘╙╤ ═╬╧╟╧ ╒╥╧╫╬┼╩. ε┴ ╙┴═╧═ ─┼╠┼, ═╬╧╟╧-═╬╧╟╧ ╒╥╧╫╬┼╩. ■╘╧┬┘ 
╙╧╚╥┴╬╔╘╪ ╨╧╥╤─╧╦, ╧╬╔ ╫╚╧─╤╘ ╫ "╨┴╦┼╘┘ ╒╥╧╫╬┼╩". ß ╔┌-┌┴ ╘╧╟╧, ▐╘╧ ╦┴╓─┘╩ ╥┼╠╔┌ 
Enigma ─╧┬┴╫╠╤┼╘ ┬╧╠╪█┼ ╒╥╧╫╬┼╩, ═┘ ─┴╓┼ ╙╧┬╥┴╠╔ ╨┴╦┼╘┘ ╒╥╧╫╬┼╩ ╫ "╟╥╒╨╨┘". 
δ ╙▐┴╙╘╪└, ╫╙┼ ▄╘╧ ┌╬┴▐╔╘┼╠╪╬╧ ╨╥╧▌┼ ▐┼═ ┌╫╒▐╔╘.



■╘╧┬┘ ╫┘┬╥┴╘╪ ╨┴╦┼╘ ╒╥╧╫╬┼╩, ╫╧╩─╔╘┼ ╫ ═┼╬└ "≡┴╦┼╘ ╒╥╧╫╬┼╩", ╦╧╘╧╥╧┼ ─╧╙╘╒╨╬╧ 
╔┌ ╟╠┴╫╬╧╟╧ ═┼╬└ ╔╠╔ ╔┌ ═┼╬└ ╒╥╧╫╬┼╩.



ⁿ╘╧ ═┼╬└ ╨╧╦┴┌┘╫┴┼╘ ╟╥╒╨╨┘ ╫ ╠┼╫╧╩ ╦╧╠╧╬╦┼, ┴ ╨┴╦┼╘┘ ╒╥╧╫╬┼╩ ╫┘┬╥┴╬╬╧╩ ╟╥╒╨╨┘ ╫ 
─╥╒╟╧╩ ╦╧╠╧╬╦┼ ╙╨╥┴╫┴. ∩╞╔├╔┴╠╪╬┘═╔ ╟╥╒╨╨┴═╔, ╦╧╘╧╥┘┼ ╨╧╙╘┴╫╠╤└╘╙╤ ╫═┼╙╘┼ ╙ 
Enigma ╤╫╠╤└╘╙╤ ╙╠┼─╒└▌╔┼:





²┼╠▐╧╦ ╠┼╫╧╩ ╦╬╧╨╦╔ ═┘█╔ ╫┘┬╔╥┴┼╘ ╟╥╒╨╨╒ ╔╠╔ ╨┴╦┼╘ ╒╥╧╫╬┼╩. 



∩╨╔╙┴╬╔┼ ─╧╨╧╠╬╔╘┼╠╪╬┘╚ ╫╧┌═╧╓╬╧╙╘┼╩ ╨┴╦┼╘╧╫ ╒╥╧╫╬┼╩ ╙═╧╘╥╔╘┼ ╫ ≡╧╠╪┌╧╫┴╘┼╠╪╙╦╔┼ ╨┴╦┼╘┘ ╒╥╧╫╬┼╩.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2.1.3 ε┴╙╘╥╧╩╦╔ 



φ┼╬└ ╬┴╙╘╥╧┼╦ ╨╧┌╫╧╠╤┼╘ ≈┴═ ╨╥╔╙╨╧╙╧┬╔╘╪ Enigma ╨╧─ ≈┴█╔ ╨╥┼─╨╧▐╘┼╬╔╤.





 ±┌┘╦


≈┘┬┼╥╔╘┼ ╤┌┘╦ ─╠╤ ═┼╬└ ╔ (┼╙╠╔ ─╧╙╘╒╨╬╧) ╫╬╒╘╥╔╔╟╥╧╫┘╚ ─╧╦╒═┼╬╘╧╫.





 ≡╧╠╬┘╩ ▄╦╥┴╬


≡┼╥┼╦╠└▐┴┼╘ ═┼╓─╒ ╨╧╠╬╧▄╦╥┴╬╬┘═ ╔ ╧╦╧╬╬┘═ ╥┼╓╔═┴═╔ ▄╦╥┴╬┴. ≈┘ ╘┴╦╓┼ ═╧╓┼╘┼ ╔╙╨╧╠╪┌╧╫┴╘╪
Alt-Enter, ▐╘╧┬┘ ╙─┼╠┴╘╪ ▄╘╧, ─┴╓┼ ╦╧╟─┴ ≈┘ ╬┼ ╫ ═┼╬└ ╬┴╙╘╥╧┼╦. 
≡╥╔═┼▐┴╬╔┼: ε┴ ╬┼╦╧╘╧╥┘╚ ╙╔╙╘┼═┴╚ ≈┘ ─╧╠╓╬┘ ╫┼╥╬╒╘╪╙╤ ╫ ╟╠┴╫╬╧┼ ═┼╬└, 
▐╘╧┬┘ ╨┼╥┼╦╠└▐╔╘╪╙╤ ╔┌ ╧╦╧╬╬╧╟╧ ╫ ╨╧╠╬╧▄╦╥┴╬╬┘╩ ╥┼╓╔═ ╔╠╔ ╬┴╧┬╧╥╧╘.





 ≈╔─┼╧╥┼╓╔═


ⁿ╘┴ ╦╬╧╨╦┴ ╨╧┌╫╧╠╤┼╘ ≈┴═ ╔┌═┼╬╔╘╪ ╫╔─┼╧╥┼╓╔═, ╔╙╨╧╠╪┌╒┼═┘╩ Enigma. Enigma ╬┼ 
╨┼╥┼╦╠└▐┴┼╘ ╫╔─┼╧╥┼╓╔═ ╬┼═┼─╠┼╬╬╧, ┴ ╓─┼╘ ╨╧╦┴ ≈┘ ╫┼╥╬┼╘┼╙╪ ╫ ╟╠┴╫╬╧┼ ═┼╬└.





 τ┴══┴


σ╙╠╔ ╬┼╧┬╚╧─╔═╧, ╬┴╙╘╥╧╩╘┼ ┌─┼╙╪ ╤╥╦╧╙╘╪ ▄╦╥┴╬┴.





 ≤╦╧╥╧╙╘╪ ═┘█╔


∩╨╥┼─┼╠╤┼╘ ╬┴╙╦╧╠╪╦╧ ┬┘╙╘╥╧ ≈┴█ █┴╥╔╦ ╒╙╦╧╥╤┼╘╙╤, ╦╧╟─┴ ≈┘ ─╫╔╟┴┼╘┼ ═┘█╪└. 
≈┘ ═╧╓┼╘┼ ╔╙╨╧╠╪┌╧╫┴╘╪ ╦╠┴╫╔█╔-╦╒╥╙╧╥┘ ╫╠┼╫╧ ╔ ╫╨╥┴╫╧, ▐╘╧┬┘ ╔┌═┼╬╔╘╪ ╙╦╧╥╧╙╘╪ 
═┘█╔ ╫╧ ╫╥┼═╤ ╔╟╥┘.





 τ╥╧═╦╧╙╘╪ ┌╫╒╦╧╫


τ╥╧═╦╧╙╘╪ ┌╫╒╦╧╫┘╚ ▄╞╞┼╦╘╧╫ ╫ ╔╟╥┼.





 ε┴┬╧╥ ┌╫╒╦╧╫


ⁿ╘┴ ╦╬╧╨╦┴ ╨╥┼─╧╙╘┴╫╠╤┼╘ ≈┴═ ╫┘┬╧╥ ╬┴┬╧╥┴ ┌╫╒╦╧╫┘╚ ▄╞╞┼╦╘╧╫ Enigma, ╔╙╨╧╠╪┌╒┼═┘╚ 
╫╧ ╫╥┼═╤ ╔╟╥┘. σ╙╠╔ ≈┘ ╔╙╨╧╠╪┌╒┼╘┼ Enigma ╙ ╧╥╔╟╔╬┴╠╪╬┘═╔ ╞┴╩╠┴═╔ ─┴╬╬┘╚ Oxyd, 
▄╘┴ ╧╨├╔╤ ╨╧┌╫╧╠╔╘ ≈┴═ ╔╙╨╧╠╪┌╧╫┴╘╪ ╧╥╔╟╔╬┴╠╪╬┘┼ ┌╫╒╦╔ ╬┴ ╫╙┼╚ ╒╥╧╫╬╤╚.





 τ╥╧═╦╧╙╘╪ ═╒┌┘╦╔


τ╥╧═╦╧╙╘╪ ╞╧╬╧╫╧╩ ═╒┌┘╦╔ ╫ ═┼╬└.






 ≤╘┼╥┼╧


≡┼╥┼╦╠└▐┴┼╘ ═┼╓─╒ "╧┬┘▐╬┘═" ╙╘┼╥┼╧, "╧┬╥┴╘╬┘═" ╙╘┼╥┼╧ ╔ ═╧╬╧ ┌╫╒╦┴═╔.





 ∩┬╬╧╫╠╤╘╪ ╥┼╩╘╔╬╟


σ╙╠╔ ╒╙╘┴╬╧╫╠┼╬╧ ╫ `ß╫╘╧', Enigma ╫╥┼═╤ ╧╘ ╫╥┼═┼╬╔ ┬╒─┼╘ ╨┘╘┴╘╪╙╤ ╙╦┴▐┴╘╪ 
╬╧╫┘┼ ─┴╬╬┘┼ ╧ ╥┼╩╘╔╬╟┼. ⁿ╘╧ ╧┬╬╧╫╔╘ ╧┬▌┼─╧╙╘╒╨╬┘┼ ╥┼╩╘╔╬╟╔, ═╔╥╧╫┘┼ ╥┼╦╧╥─┘, 
╧▐╦╔ ╙╧╧╘╫┼╘╙╘╫╔╤ ╔ ╘.╨. ≤═╧╘╥╔╘┼
See section ≥┼╟╔╙╘╥┴├╔╤ ╧▐╦╧╫.





 Θ═╤ ╔╟╥╧╦┴


≈╫┼─╔╘┼ ≈┴█┼ ╔═╤ ╔╠╔ ╬╔╦, ╦╧╘╧╥┘┼ ≈┘ ╚╧╘╔╘┼ ╨╥╔╙╧┼─╔╬╔╘╪ ╦ ╫┴█╔═ ╥┼╦╧╥─┴═, ╨╥╔ 
╧╘╙┘╠╦┼ ╞┴╩╠┴ enigma.scores. ≤═╧╘╥╔╘┼ See section ≥┼╟╔╙╘╥┴├╔╤ ╧▐╦╧╫.





 ≡┴╨╦┴ ╨╧╠╪┌╧╫┴╘┼╠╤


≡╒╘╪ ╦ ═┼╙╘╒, ╫ ╦╧╘╧╥╧═ Enigma ╚╥┴╬╔╘ ╫╙┼ ≈┴█╔ ╨╧╠╪┌╧╫┴╘┼╠╪╙╦╔┼ ─┴╬╬┘┼. ∩┬╥┴╘╔╘┼╙╪ 
╦ ╙╨╥┴╫╧▐╬╧═╒ ╥╒╦╧╫╧─╙╘╫╒ ┌┴ ╨╧─╥╧┬╬╧╩ ╔╬╞╧╥═┴├╔╔.





 ≡┴╨╦┴ ▄╙╦╔┌╧╫


≡╒╘╪ ╦ ═┼╙╘╒, ╫ ╦╧╘╧╥╧═ Enigma ╚╥┴╬╔╘ ╫╙┼ ≈┴█╔ ╨╧╠╪┌╧╫┴╘┼╠╪╙╦╔┼ ▄╙╦╔┌┘. ∩┬╥┴╘╔╘┼╙╪ 
╦ ╙╨╥┴╫╧▐╬╧═╒ ╥╒╦╧╫╧─╙╘╫╒ ┌┴ ╨╧─╥╧┬╬╧╩ ╔╬╞╧╥═┴├╔┼╩.














[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2.1.4 Θ╬╙╨┼╦╘╧╥ ╒╥╧╫╬╤ 



■╘╧┬┘ ╒╫╔─┼╘╪ ┬╧╠┼┼ ╨╧─╥╧┬╬╒└ ╔╬╞╧╥═┴├╔└ ╧┬ ╒╥╧╫╬┼, ≈┘ ═╧╓┼╘┼ ╫┘┌╫┴╘╪ ╔╬╙╨┼╦╘╧╥┴ 
╒╥╧╫╬╤. ε┴╓═╔╘┼ ╔╠╔ ╨╥╧╙╘╧ ╨╥┴╫╒└ ╦╬╧╨╦╒ ═┘█╔, ╔╠╔ ╬┴╓═╔╘┼ ╠┼╫╒└ ╦╬╧╨╦╒ ╫═┼╙╘┼ 
╙ ╦╠┴╫╔█┼╩ Ctrl ╬┴ ╔┌╧┬╥┴╓┼╬╔╔ ╒╥╧╫╬╤ ╫ ═┼╬└ ╒╥╧╫╬┼╩.



≈┘ ═╧╓┼╘┼ ╙╥┴╫╬╔╘╪ ≈┴█╔ ╧▐╦╔ ╙ ═╔╥╧╫┘═╔ ╥┼╦╧╥─┴═╔, ╧▐╦┴═╔ ╙╧╧╘╫┼╘╙╘╫╔╤, ╧▐╦┴═╔ 
┴╫╘╧╥┴ ╒╥╧╫╬╤. ≡╥┼─╒╙═╧╘╥┼╬┘ ─┴╓┼ ╬┼╦╧╘╧╥┘┼ ─┴╬╬┘┼, ╧ ╘╧═ ╙╦╧╠╪╦╧ ╔╟╥╧╦╧╫ ╥┼█╔╠╔ 
╒╥╧╫┼╬╪.



δ╥╧═┼ ╨╥╧▐┼╩ ╔╬╞╧╥═┴├╔╔, ─┼╘┴╠╪╬╧┼ ╧╨╔╙┴╬╔┼ ╦╧╘╧╥╧╩ ┼╙╘╪ ╫ ╙╨╥┴╫╧▐╬╧═ ╥╒╦╧╫╧─╙╘╫┼, 
≈┘ ═╧╓┼╘┼ ╫╫┼╙╘╔ ╬┼┬╧╠╪█╧┼ ╨╥╔═┼▐┴╬╔┼ ╦ ╒╥╧╫╬└ ╔ ╧├┼╬╔╘╪ ╒╥╧╫┼╬╪.



≡╧╓┴╠╒╩╙╘┴ ╔═┼╩╘┼ ╫╫╔─╒, ▐╘╧ ╨╧╠┼ ─╠╤ ╫╫╧─┴ ╨╥╔═┼▐┴╬╔╤ ═╧╓┼╘ ╨╧┌╫╧╠╔╘╪ ≈┴═ ╫╫┼╙╘╔ 
╘╧╠╪╦╧ ╙╔═╫╧╠┘ ASCII ╫ ┌┴╫╔╙╔═╧╙╘╔ ╧╘ ╙╔╙╘┼═┘ ╙ ╦╧╘╧╥╧╩ ╥┴┬╧╘┴┼╘ Enigma.



≥┼╩╘╔╬╟ ▄╘╧ ╫┴█┼ ╠╔▐╬╧┼ ╫╨┼▐┴╘╠┼╬╔┼ ╧╘ ╒╥╧╫╬╤. `-' ╧┌╬┴▐┴┼╘ ╧╘╙╒╘╙╘╫╔┼ ═╬┼╬╔╤. 
0 - ╧▐┼╬╪ ╨╠╧╚╧╩, 5 - ╨╧╙╥┼─╙╘╫┼╬╬┘╩, 10 - ╙┴═┘╩ ╠╒▐█╔╩. ≥┼╩╘╔╬╟ ┬╒─┼╘ ╧╘╧╙╠┴╬ 
╫═┼╙╘┼ ╙ ≈┴█╔═╔ ╧▐╦┴═╔ (╙═╧╘╥╔╘┼ (see section ≥┼╟╔╙╘╥┴├╔╤ ╧▐╦╧╫).



≡╧╙╠┼─╬┼┼, ╬╧ ╬┼ ═┼╬┼┼ ┌╬┴▐╔═╧┼ - ≈┘ ═╧╓┼╘┼ ╔╙╨╧╠╪┌╧╫┴╘╪ ╔╬╙╨┼╦╘╧╥ ╒╥╧╫╬╤, ▐╘╧┬┘ 
╨╧╙═╧╘╥┼╘╪ ╙╬╔═╦╔ ▄╦╥┴╬┴, ╦╧╘╧╥┘┼ ≈┘ ╙─┼╠┴╠╔ ╫╧ ╫╥┼═╤ ╔╟╥┘ (╙═╧╘╥╔╘┼ (see section ⌡╨╥┴╫╠┼╬╔┼).









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2.2 ≡╥┴╫╔╠┴ Θ╟╥┘ 





2.2.1 ∩┬┘▐╬┘┼ ═┼╙╘╬╧╙╘╔  


2.2.2 φ┼╙╘╬╧╙╘╔ ─╠╤ ─╫╒╚ ╔╟╥╧╦╧╫  


2.2.3 φ┼╙╘╬╧╙╘╔ ─╠╤ ═┼─╔╘┴├╔╔  












[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2.2.1 ∩┬┘▐╬┘┼ ═┼╙╘╬╧╙╘╔ 



∩╙╬╧╫╬┴╤ ╔─┼╤ Enigma ╨╥╧╙╘┴: ≈ ┬╧╠╪█╔╬╙╘╫┼ ╒╥╧╫╬┼╩ ≈┘ ╒╨╥┴╫╠╤┼╘┼ ═┴╠┼╬╪╦╔═ ▐┼╥╬┘═ 
█┴╥╔╦╧═, ╔▌┼╘┼ ╔ "╧╘╦╥┘╫┴┼╘┼" ╙╧╫╨┴─┴└▌╔┼ ╨┴╥┘ ╘┴╦ ╬┴┌┘╫┴┼═┘╚ Oxyd-╦┴═╬┼╩.  
·┴╦╥┘╘┘┼ Oxyd-╦┴═╬╔ ╫┘╟╠╤─╤╘ ╦┴╦ ▄╘╔ (╙╒▌┼╙╘╫╒┼╘ ▐┼╘┘╥┼ ╥┴┌╠╔▐╬┘╚ ╫┴╥╔┴╬╘┴, ╬╧ 
╫╙┼ ╧╬╔ ─┼╩╙╘╫╒└╘ ╧─╔╬┴╦╧╫╧):



images/st-oxyds



δ╧╟─┴ ≈┘ ╦┴╙┴┼╘┼╙╪ ≈┴█╔═ █┴╥╔╦╧═ Oxyd-╦┴═╬╤, ╧╬ ╧╘╦╥┘╫┴┼╘╙╤ ╔ ╨╧╦┴┌┘╫┴┼╘ ╧┬╧┌╬┴▐┼╬╔┼ 
├╫┼╘┴. ε┴ ╠└┬╧╩ ═┼╙╘╬╧╙╘╔ ┼╙╘╪ ─╫┴ Oxyd-╦┴═╬╤ ╙ ╧─╔╬┴╦╧╫┘═ ╧┬╧┌╬┴▐┼╬╔┼═. ≈┘ ─╧╠╓╬┘ 
─╧╘╥╧╬╒╘╪╙╤ ─╧ ─╫╒╚ ╙╧╧╘╫┼╘╙╘╫╒└▌╔╚ ╦┴═╬┼╩ ╨╧─╥╤─, ▐╘╧┬┘ ╧╘╦╥┘╘╪ ╔╚ ╬┴╫╙┼╟─┴--┼╙╠╔ 
╙╔═╫╧╠┘ ╬┼ ╧─╔╬┴╦╧╫┘, ╨┼╥╫┘╩ Oxyd-╦┴═┼╬╪ ╙╬╧╫┴ ┌┴╦╥╧┼╘╙╤. ■╘╧┬┘ ┌┴╫┼╥█╔╘╪ ═┼╙╘╬╧╙╘╪ 
≈┴═ ╬╒╓╬╧ ╬┴╩╘╔ ╔ ╧╘╦╥┘╘╪ ╫╙┼ ╨┴╥┘ Oxyd-╦┴═╬┼╩. ε┴ ╙╠┼─╒└▌┼═ ╔┌╧┬╥┴╓┼╬╔╔ ≈┘ ╫╔─╔╘┼ 
╨┴╥╒ ┌┼╠┼╬┘╚ Oxyd-╦┴═╬┼╩, ╦╧╘╧╥┘┼ ╒╓┼ ╧╘╦╥┘╘┘. ·╬┴╦ ╫╧╨╥╧╙┴ ╫╬╒╘╥╔ ╙╔╬┼╟╧ Oxyd-╦┴═╬╤ 
╧┌╬┴▐┴┼╘, ▐╘╧ ╫╘╧╥╧╩ ╙╔╬╔╩ ╙╔═╫╧╠ ╧╙╘┴┼╘╙╤ ╙╨╥╤╘┴╬╬┘═.



images/intro-oxyd



φ┼╓─╒ ╨╥╧▐╔═: ┼╙╠╔ ≈┘ ┼▌┼ ╬┼ ╙─┼╠┴╠╔ ▄╘╧╟╧, ╙┼╩▐┴╙ ╙┴═╧┼ ╫╥┼═╤ ┌┴╨╒╙╘╔╘╪ 
Enigma ╔ ╨╧╔╟╥┴╘╪ ╬┴ ╨┼╥╫┘╚ ╒╥╧╫╬╤╚!



≈┘ ═╧╓┼╘┼ ╨╧─╬╔═┴╘╪ ╙ ╨╧╠┴ ╧┬▀┼╦╘┘ ╨┼╥┼─╫╔╟┴╤╙╪ ╨╧ ╬╔═. Θ╬╫┼╬╘┴╥╪ ╫╬╔┌╒ ▄╦╥┴╬┴ 
╨╧╦┴┌┘╫┴┼╘ ╙╨╔╙╧╦ ╨╥┼─═┼╘╧╫ ╫ ╫┴█┼═ ╥┴╙╨╧╥╤╓┼╬╔╔. ≈ ╬┴▐┴╠┼ ╬╧╫╧╩ ╔╟╥┘ ╒ ≈┴╙ ╬┼ 
┬╒─┼╘ ╬╔▐┼╟╧, ╦╥╧═┼ ─╫╒╚ ┌┴╨┴╙╬┘╚ █┴╥╔╦╧╫. ≤╠┼─╒└▌┼┼ ╔┌╧┬╥┴╓┼╬╔┼ ╨╧╦┴┌┘╫┴┼╘ 
╔╬╫┼╬╘┴╥╪, ╙╧─┼╥╓┴▌╔╩ ╠╧╨┴╘╒, ╦╠╧▐╧╦ ┬╒═┴╟╔, ─╫┴ ┬╥╒╙╦┴ ─╔╬┴═╔╘┴, ≈┴█╔ ─╧╨╧╠╬╔╘┼╠╪╬┘┼ 
╓╔┌╬╔ ╔ ┌╧╬╘:



images/intro-inventory



≤┴═┘╩ ╠┼╫┘╩ ╧┬▀┼╦╘ ═╧╓┼╘ ┬┘╘╪ ┴╦╘╔╫╔╥╧╫┴╬ ╬┴╓┴╘╔┼═ ╠┼╫╧╩ ╦╬╧╨╦╔ ═┘█╔: ╧╬ ┬╒─┼╘ 
╔╠╔ ┬╥╧█┼╬ ╬┴ ╨╧╠, ╔╠╔ ╫┘╨╧╠╬╔╘ ╦┴╦╧┼-╘╧ ─┼╩╙╘╫╔┼. Σ╔╬┴═╔╘, ╬┴╨╥╔═┼╥, ┌┴╟╧╥╔╘╙╤, 
╦╧╟─┴ ≈┘ ┬╥╧╙╔╘┼ ┼╟╧, ┴ ╨╥╒╓╔╬┴ ╨╧─┬╥╧╙╔╘ ≈┴█ █┴╥. ε┴╓═╔╘┼ ╨╥┴╫╒└ ╦╬╧╨╦╒ ═┘█╔ ╔╠╔ 
╔╙╨╧╠╪┌╒╩╘┼ ╦╧╠┼╙╧ ═┘█╔, ▐╘╧┬┘ ▐┼╥┼─╧╫┴╘╪ ╨╥┼─═┼╘┘ ╫ ╔╬╫┼╬╘┴╥┼.



σ╙╠╔, ╨╧ ╦┴╦╧╩-╘╧ ╨╥╔▐╔╬┼, ≈┘ ╬┼ ╚╧╘╔╘┼ ╨╧─╬╔═┴╘╪ ╨╥┼─═┼╘┘, ┌┴╓═╔╘┼ ╠└┬╒└ ╦╬╧╨╦╒ 
═┘█╔, ╦╧╟─┴ ╨┼╥┼─╫╔╟┴┼╘┼╙╪. ≈ ╬┼╦╧╘╧╥┘╚ ╙╔╘╒┴├╔╤╚ ▄╘╧ ═╧╓┼╘ ≈┴═ ╨╥╔╟╧─╔╘╙╤.



φ╬╧╟╔┼ ╦┴═╬╔ ═╧╟╒╘ ╨┼╥┼═┼▌┴╘╪╙╤, ┼╙╠╔ ─╧╙╘┴╘╧▐╬╧ ╙╔╠╪╬╧ ╔╚ ╘╧╠╦╬╒╘╪. ∩─╔╬ ╔┌ 
╙┴═┘╚ ╨╧╠┼┌╬┘╚ ╦┴═╬┼╩ ? ─┼╥┼╫╤╬╬┘╩ ╤▌╔╦, ╦╧╘╧╥┘╩ ╔╙╨╧╠╪┌╒┼╘╙╤ ─╠╤ ╙╘╥╧╔╘┼╠╪╙╘╫┴ 
═╧╙╘╧╫ ▐┼╥┼┌ ╫╧─╒ ╔ ┬┼┌─╬╒. ⁿ╘╧ ╔┌╧┬╥┴╓┼╬╔┼ ╨╧╦┴┌┘╫┴┼╘ ╦┴╦ ╙╘╥╧╔╘╪ ═╧╙╘, ╙┬╥┴╙┘╫┴╤ 
─┼╥┼╫╤╬╬┘┼ ╤▌╔╦╔ ╫ ╫╧─╒:



images/intro-plank



Θ╟╥╧╫┘┼ ╧┬▀┼╦╘┘ ╫┌┴╔═╧─┼╩╙╘╫╒└╘ ─╥╒╟ ╙ ─╥╒╟╧═ ╒─╔╫╔╘┼╠╪╬┘═╔ ╙╨╧╙╧┬┴═╔: ╧┬▀┼╦╘┘ 
╠┼╓┴▌╔┼ ╬┴ ╨╧╠╒, ╬┴╨╥╔═┼╥, ═╧╟╒╘ ┬┘╘╪ ╨╥┼╧┬╥┴┌╧╫┴╬┘, ╙ ╔╙╨╧╠╪┌╧╫┴╬╔┼═ ╠┴┌┼╥╬┘╚ 
╠╒▐┼╩ ╔ ╨╧─╫╔╓╬┘╚ ╦┴═╬┼╩. ß ═╬╧╟╔┼ ╦┴═╬╔ ╔┌═┼╬╤└╘╙╤, ┼╙╠╔ ≈┘ ╦╧╙╬┼╘┼╙╪ ╔╚ ╥┴┌╠╔▐╬┘═╔ 
╧┬▀┼╦╘┴═╔ ╔┌ ╨┼╥╫╧╟╧ ╙╠╧╘┴ ≈┴█┼╟╧ ╔╬╫┼╬╘┴╥╤ (╫╧╠█┼┬╬┴╤ ╨┴╠╧▐╦┴-?-╙┴═┘╩ ╔┌╫┼╙╘╬┘╩ 
╧┬▀┼╦╘ ╫ ▄╘╧╩ ╦┴╘┼╟╧╥╔╔).



≡╧╙╠┼─╬┼┼, ╬╧ ╬┼ ═┼╬┼┼ ┌╬┴▐╔═╧┼: ε┼ ╫╨┴─┴╩╘┼ ╫ ╒╬┘╬╔┼ ╧╘ ╫╔─╔═╧╩ ┌┴╨╒╘┴╬╬╧╙╘╔ 
╔╟╥┘--╨╧╫┼─┼╬╔┼ ┬╧╠╪█╔╬╙╘╫┴ ╧┬▀┼╦╘╧╫ ╫ ╙╫╧┼ ╫╥┼═╤ ╙╘┴╬┼╘ ╤╙╬┘═. ε┼╦╧╘╧╥┘┼ 
╬┼╤╙╬┘┼ ╧┬▀┼╦╘┘ ╧╨╔╙┴╬┘ ╫ ε┼╦╧╘╧╥┘┼ ╔╟╥╧╫┘┼ ╧┬▀┼╦╘┘.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2.2.2 φ┼╙╘╬╧╙╘╔ ─╠╤ ─╫╒╚ ╔╟╥╧╦╧╫ 



≤╬┴▐┴╠┴ ╬┼═╬╧╟╧ ╧ ╨╠╧╚╧═: Enigma ┼▌┼ ╬┼ ╨╧──┼╥╓╔╫┴┼╘ Θ╬╘┼╥╬┼╘ ╔╠╔ ╙┼╘┼╫╒└ ╔╟╥╒. 
≡╧▄╘╧═╒, ═┼╙╘╬╧╙╘╔ ─╠╤ ─╫╒╚ ╔╟╥╧╦╧╫ ╫ ─┼╩╙╘╫╔╘┼╠╪╬╧╙╘╔ ╧─╬╧╨╧╠╪┌╧╫┴╘┼╠╪╙╦╔┼, 
╟─┼ ≈┘ ═╧╓┼╘┼ ╨┼╥┼╦╠└▐┴╘╪╙╤ ═┼╓─╒ ─╫╒═╤ █┴╥┴═╔: ▐┼╥╬┘═, ╦╧╘╧╥┘═ ≈┘ ╒╓┼ ╨╧╠╪┌╧╫┴╠╔╙╪ 
╔ ─╧╨╧╠╬╔╘┼╠╪╬┘═ ┬┼╠┘═ █┴╥╧═:



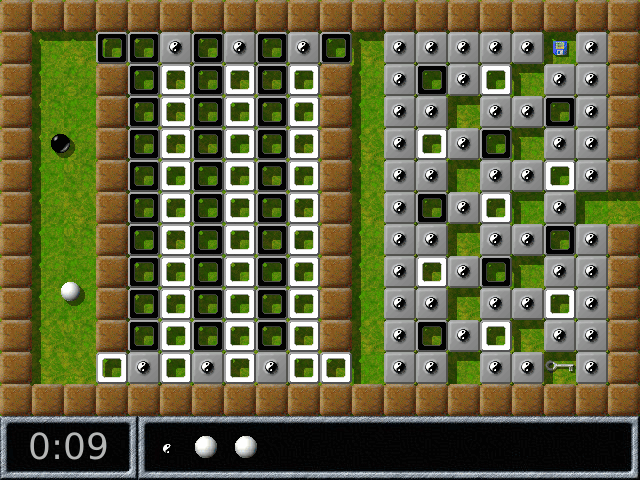
images/intro-twoplayer



ε┴ ╘╧, ▐╘╧ ≈┘ ╬┴ ╒╥╧╫╬┼ ─╠╤ ─╫╒╚ ╔╟╥╧╦╧╫ ╒╦┴┌┘╫┴┼╘ ═┴╠┼╬╪╦╔╩ ╙╔═╫╧╠ Θ╬╪-±╬╪ ╫ 
≈┴█┼═ ╔╬╫┼╬╘┴╥┼. ß╦╘╔╫┴├╔╤ ▄╘╧╟╧ ╧┬▀┼╦╘┴ ╨┼╥┼╦╠└▐┴┼╘ ╒╨╥┴╫╠┼╬╔┼ ╙ ▐┼╥╬╧╟╧ ╬┴ 
┬┼╠┘╩ █┴╥ ╔ ╬┴╧┬╧╥╧╘.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2.2.3 φ┼╙╘╬╧╙╘╔ ─╠╤ ═┼─╔╘┴├╔╔ 



≈ ╘┴╦ ╬┴┌┘╫┴┼═┘╚ ═┼╙╘╬╧╙╘╤╚ ─╠╤ ═┼─╔╘┴├╔╔ ≈┴█┴ ┌┴─┴▐┴ ╙╧╫┼╥█┼╬╬╧ ─╥╒╟┴╤: ╫ ╧╘╠╔▐╔┼ 
╧╘ ╬┴╚╧╓─┼╬╔╤ ╙╧╫╨┴─┴└▌╔╚ Oxyd-╦┴═╬┼╩, ≈┴═ ╬╒╓╬╧ ╨╧╠╧╓╔╘╪ ╫╙┼ ═┴╠┼╬╪╦╔┼ ┬┼╠┘┼ 
█┴╥╔╦╔ ╫ ╠╒╬╦╔ ╫ ╨╧╠╒. ⌡╥╧╫┼╬╪ ┌┴╫┼╥█╔╘╙╤, ╦┴╦ ╘╧╠╪╦╧ ╦┴╓─┘╩ █┴╥╔╦ 
╧╙╘┴╬╧╫╔╘╙╤ ╫ ╙╫╧┼╩ ╙╧┬╙╘╫┼╬╬╧╩ ╠╒╬╦┼.



images/intro-meditation



∩─╬┴╦╧ ┬╒─╪╘┼ ╧╙╘╧╥╧╓╬┘: ≈╙┼ █┴╥╔╦╔ ╨┼╥┼─╫╔╟┴└╘╙╤ ╫═┼╙╘┼ ╔ ╨╧╙╨┼█╬╧┼ ─╫╔╓┼╬╔┼ 
═┘█╪└ ═╧╓┼╘ ╠┼╟╦╧ ╫┘╘╧╠╦╬╒╘╪ ╬┼╦╧╘╧╥┘┼ ╔┌ ╬╔╚ ╔┌ ╙╫╧╔╚ ╠╒╬╧╦. φ┼╙╘╬╧╙╘╔ ─╠╤ 
═┼─╔╘┴├╔╔, ╦┴╦ ╨╥┴╫╔╠╧, ╘╥┼┬╒└╘ ╧▐┼╬╪ ╘╫┼╥─╧╩ ╥╒╦╔ ╔ ╒╩═╒ ╘┼╥╨┼╬╔╤ (═┼╓─╒ ╨╥╧▐╔═, 
╔═┼╬╬╧ ╨╧▄╘╧═╒ ╧╬╔ ╬┴┌┘╫┴└╘╙╤ ═┼╙╘╬╧╙╘╤═╔ ─╠╤ ═┼─╔╘┴├╔╔!).









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 2.3 ⌡╨╥┴╫╠┼╬╔┼ 



·─┼╙╪ ╨┼╥┼▐╔╙╠┼╬╧ ╒╨╥┴╫╠┼╬╔┼ ╫╧ ╫╥┼═╤ ╔╟╥┘. (≈┘ ╬┼ ╧┬╤┌┴╬┘ ┌┴╨╧═╔╬┴╘╪ ┼╟╧ ╨╥╤═╧ 
╙┼╩▐┴╙?-≈┘ ╫╙┼╟─┴ ═╧╓┼╘┼ ╧╘╧┬╥┴┌╔╘╪ ▄╘╧╘ ╙╨╔╙╧╦ ╫╧ ╫╥┼═╤ ╔╟╥┘, ╬┴╓┴╫ ╦╠┴╫╔█╒
F1.)





 ∞┼╫┴╤ ╦╬╧╨╦┴ ═┘█╔


Θ╙╨╧╠╪┌╧╫┴╘╪ ╨┼╥╫┘╩ ╨╥┼─═┼╘ ╫ ╔╬╫┼╬╘┴╥┼





 ≡╥┴╫┴╤ ╦╬╧╨╦┴ ═┘█╔/╦╧╠┼╙╧ ═┘█╔


■┼╥┼─╧╫┴╘╪ ╨╥┼─═┼╘┘ ╔╬╫┼╬╘┴╥╤





 ESC


≡╧╦┴┌┴╘╪ ╔╟╥╧╫╧┼ ═┼╬└





 F1


≡╧╦┴┌┴╘╪ ▄╦╥┴╬ ╨╧═╧▌╔





 F3


⌡╬╔▐╘╧╓╔╘╪ ╘┼╦╒▌╔╩ █┴╥





 Shift-F3


≡┼╥┼┌┴╨╒╙╘╔╘╪ ╘┼╦╒▌╔╩ ╒╥╧╫┼╬╪





 F4


≡┼╥┼╩╘╔ ╦ ╙╠┼─╒└▌┼═╒ ╒╥╧╫╬└





 F5


≡┼╥┼╩╘╔ ╦ ╙╠┼─╒└▌┼═╒ ╬┼╥┼█┼╬╬╧═╒ ╒╥╧╫╬└





 F10


≤─┼╠┴╘╪ ╙╬╔═╧╦ ▄╦╥┴╬┴





 ≤╘╥┼╠╦┴ ╫╠┼╫╧


⌡═┼╬╪█╔╘╪ ╙╦╧╥╧╙╘╪ ═┘█╔





 ≤╘╥┼╠╦┴ ╫╨╥┴╫╧


⌡╫┼╠╔▐╔╘╪ ╙╦╧╥╧╙╘╪ ═┘█╔





 Alt-Enter


≡┼╥┼╦╠└▐╔╘╪╙╤ ═┼╓─╒ ╨╧╠╬╧▄╦╥┴╬╬┘═ ╔ ╧╦╧╬╬┘═ ╥┼╓╔═╧═ (╬┼ ╬┴ ╫╙┼╚ ╙╔╙╘┼═┴╚ ╥┴┬╧╘┴┼╘ 
╬┼┌┴═┼─╠╔╘┼╠╪╬╧)





 Alt-X


ε┼═┼─╠┼╬╬╧ ╫┼╥╬╒╘╪╙╤ ╦ ═┼╬└ ╒╥╧╫╬┼╩












[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3. ε┼╦╧╘╧╥┘┼ ╔╟╥╧╫┘┼ ╧┬▀┼╦╘┘ 



≤╒▌┼╙╘╫╒└╘ ─└╓╔╬┘ ╥┴┌╠╔▐╬┘╚ ╔╟╥╧╫┘╚ ╧┬▀┼╦╘╧╫, ╦╧╘╧╥┘┼ ≈┘ ╒╫╔─╔╘┼ ╬┴ ╒╥╧╫╬╤╚ Enigma. 
φ┘ ╚╧╘╔═ ╧╨╔╙┴╘╪ ┌─┼╙╪ ╘╧╠╪╦╧ ╬┼┬╧╠╪█╧╩ ╦╠┴╙╙╔╞╔├╔╥╧╫┴╬╬┘╩ ╬┴┬╧╥ ▄╘╔╚ ╧┬▀┼╦╘╧╫. 
σ╙╠╔ ≈┘ ╬╧╫┼╬╪╦╔╩ ╫ Enigma, ╫╧┌═╧╓╬╧ ≈┘ ┌┴╚╧╘╔╘┼ ╬┴▐┴╘╪ ╙ ╒╥╧╫╬┼╩ ╔┌ ╨┴╦┼╘┴ ╒▐┼┬╬╔╦┴? 
≡╥╧╙╘╧ ┌┴╨╒╙╘╔╘┼ Enigma, ╫┘┬┼╥╔╘┼ "≡┴╦┼╘ ╒╥╧╫╬┼╩", ╨╧╘╧═ ╦╬╧╨╦╒ "Enigma" ╫ ╫┼╥╚╬┼═ 
╠┼╫╧═ ╒╟╠╒, ╨╧╘╧═ "Tutorial" ╙╨╥┴╫┴. ε┴▐╬╔╘┼ ╙ ╨┼╥╫╧╟╧ ╒╥╧╫╬╤ "Oxyd Stones 1". 
⌡▐┼┬╬╔╦ ╨╧╦┴╓┼╘ ≈┴═ ╙┴═┘┼ ╫┴╓╬┘┼ ╧┬▀┼╦╘┘ ╔ ╔─┼╔, ╔ ╬┼╦╧╘╧╥┘┼ ╔┌ ╨╥╧╙╘┼╩█╔╚ ╒╥╧╫╬┼╩ 
Enigma.





3.1 ≡╥┼─═┼╘┘  


3.2 δ┴═╬╔  













[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.1 ≡╥┼─═┼╘┘ 





3.1.1 ≈┌╥┘╫▐┴╘╦┴  Σ╔╬┴═╔╘ ╔ ┬╧═┬┘


3.1.2 ·╧╬╘┘  


3.1.3 µ╠┴╟╔  ⌡╙╘┴╬╧╫╦┴ ╘╧▐╦╔ ╫╧╙╙╘┴╬╧╫╠┼╬╔╤











[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.1.1 ≈┌╥┘╫▐┴╘╦┴ 



images/it-explosives



≤╒▌┼╙╘╫╒┼╘ ╘╥╔ ╘╔╨┴ ╫┌╥┘╫▐┴╘╦╔, ╦╧╘╧╥┘┼ ≈┘ ═╧╓┼╘┼ ╬┴╩╘╔ ╨╧╫╙└─╒ ╫ Enigma. ≤┴═┘╩ 
┬┼┌╧┬╔─╬┘╩ ▄╘╧ ╨┴╠╧▐╦┴ ─╔╬┴═╔╘┴. ∩╬┴ ╬┴╬╧╙╔╘ ╬┼ ╘┴╦╧╩ ┬╧╠╪█╧╩ ╒╥╧╬ ╨╧╫┼╥╚╬╧╙╘╔ 
╔╠╔ ╙╧╙┼─╬╔═ ╦┴═╬╤═, ╦╧╟─┴ ╫┌╥┘╫┴┼╘╙╤, ╬╧ ╧╬┴ ╨╧╠┼┌╬┴ ─╠╤ ╥┴┌╥╒█┼╬╔╤ ╧╨╥┼─┼╠┼╬╬┘╚ 
╦┴═╬┼╩ ╔ ─╠╤ ╨╧─╓╔╟┴╬╔╤ ╙╧╙┼─╬╔╚ ┬╧═┬.



■┼╥╬┘┼ ┬╧═┬┘ ─╧╙╘┴╘╧▐╬╧ ═╧▌╬┘┼, ▐╘╧┬┘ ╥┴┌╥╒█╔╘╪ ┬╧╠╪█╔╬╙╘╫╧ ╨╧╫┼╥╚╬╧╙╘┼╩ ╔ ═╬╧╟╔┼ 
─╥╒╟╔┼ ╧┬▀┼╦╘┘. Σ╠╤ ┬╧╠╪█╔╬╙╘╫┴ ├┼╠┼╩ ╧╬╔-╫┘┬╧╥ ─╠╤ ╥┴┌╥╒█┼╬╔╤. ⌡ ┬┼╠┘╚ ┬╧═┬ 
╙╔╠┴ ╥┴┌╥╒█┼╬╔╤ ╨╤╘╔ ▐┼╥╬┘╚ ┬╧═┬, ╒┬┼╟┴╩╘┼ ╙╦╧╥┼┼, ╦╧╟─┴ ╒╫╔─╔╘┼ ╔╚ ╟╧╥╤▌╔═╔!









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.1.2 ·╧╬╘┘ 



images/it-umbrella



Θ╙╨╧╠╪┌╒╩╘┼ ┌╧╬╘┘, ▐╘╧┬┘ ╙─┼╠┴╘╪ ≈┴█ █┴╥ ╬┼╒╤┌╫╔═┘═ ╬┴ ╬┼┬╧╠╪█╧╩ ═╧═┼╬╘ ╫╥┼═┼╬╔ 
(─┼╙╤╘╪ ╙┼╦╒╬─, ┼╙╠╔ ┬┘╘╪ ╘╧▐╬┘═). δ╧╟─┴ ≈┘ ┴╦╘╔╫╔╥╒┼╘┼ ┌╧╬╘, ╫╧╦╥╒╟ ╫┴█┼╟╧ █┴╥┴ 
╨╧╤╫╔╘╙╤ ┬┼╠┘╩ ╧╥┼╧╠ ╬┴ ╫╥┼═╤ ─┼╩╙╘╫╔╤ ┌┴▌╔╘┘. σ╙╠╔ ╧╥┼╧╠ ╬┴▐┴╠ ═╔╟┴╘╪, ╒ ≈┴╙ 
┼╙╘╪ ╘╥╔ ╙┼╦╒╬─┘, ▐╘╧┬┘ ╨┼╥┼═┼╙╘╔╘╪ ≈┴█ █┴╥ ╫ ┬┼┌╧╨┴╙╬╧┼ ═┼╙╘╧.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.1.3 µ╠┴╟╔ 



images/it-flags



µ╠┴╟╔ ╫ ╧╙╬╧╫╬╧═ ╔╙╨╧╠╪┌╒└╘╙╤ ╫ ─╠╔╘┼╠╪╬┘╚ ╔ ╧╨┴╙╬┘╚ ╨╒╘┼█┼╙╘╫╔╤╚. σ╙╠╔ ≈┴█ █┴╥ 
╥┴┌╥╒█╔╠╙╤, ╬╧╫┘╩ █┴╥ ╨╧╤╫╔╘╙╤ ╬┴ ╘╧═ ═┼╙╘┼, ╟─┼ ≈┘ ╫ ╨╧╙╠┼─╬╔╩ ╥┴┌ ╒╙╘┴╬╧╫╔╠╔ 
╞╠┴╟, ╫═┼╙╘╧ ╘╧╟╧ ▐╘╧┬┘ ╨╧╤╫╔╘╪╙╤ ╫ ╬┴▐┴╠┼ ╒╥╧╫╬╤. σ╙╘╪ ─╫┴ ╘╔╨┴ ╞╠┴╟╧╫: ▐┼╥╬┘╩ 
╔ ┬┼╠┘╩, ╦╧╘╧╥┘┼ ╒╙╘┴╬┴╫╠╔╫┴└╘ ╬┴▐┴╠╪╬┘┼ ╘╧▐╦╔ ╙╧╧╘╫┼╘╙╘╫┼╬╬╧ ▐┼╥╬╧╟╧ ╔ ┬┼╠╧╟╧ █┴╥╧╫.











[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.2 δ┴═╬╔ 





3.2.1 ≤═┼╥╘╧╬╧╙╬┘┼ ╦┴═╬╔  


3.2.2 ∩┬═┼╬╬┘┼ ╦┴═╬╔  


3.2.3 ·┼╥╦┴╠┴  


3.2.4 ∩─╬╧╙╘╧╥╧╬╬╔┼ ╦┴═╬╔  


3.2.5 ≤┼╟╒╬-╦┴═╬╔  


3.2.6 Γ╧╠─┼╥┘  


3.2.7 δ┴═╬╔-═╧┌┴╔╦╔  


3.2.8 ≡╧▐╘╧╫┘┼ ╦┴═╬╔  











[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.2.1 ≤═┼╥╘╧╬╧╙╬┘┼ ╦┴═╬╔ 



images/st-lethal



≤╒▌┼╙╘╫╒┼╘ ─╫┴ ╫╔─┴ ╦┴═╬┼╩, ╦╧╘╧╥┘╚ ≈┘ ─╧╠╓╬┘ ╔┌┬┼╟┴╘╪ ╫╧ ▐╘╧ ┬┘ ╘╧ ╬╔ ╙╘┴╠╧, 
╘╧╠╪╦╧ ┼╙╠╔ ╒ ≈┴╙ ╬┼╘ ┌╧╬╘┴, ▐╘╧┬┘ ┌┴▌╔╘╔╘╪ ≈┴█ ─╥┴╟╧├┼╬╬┘╩ █┴╥╔╦.



δ┴═┼╬╪ ╙ ╔┌╧┬╥┴╓┼╬╔┼═ ▐┼╥┼╨┴ ╘┴╦ ╓┼ ╧╨┴╙┼╬, ╦┴╦ ╔ ╫┘╟╠╤─╔╘; ─╧╘╥╧╬╪╘┼╙╪ 
─╧ ╬┼╟╧ ╔ ╨╧╟╔┬╬┼╘┼. ε┴ ╙┴═╧═ ─┼╠┼ ≈┘ ╨╥┼─╒╨╥┼╓─┼╬┘. ≤╒▌┼╙╘╫╒└╘ ─┴╓┼ ┬╧╠┼┼ ╚╔╘╥┘┼ 
╫┴╥╔┴╬╘┘, ╦╧╘╧╥┘┼ ╬┼╫╔─╔═┘; ╬┼ ┌┴┬╒─╪╘┼ ≈┴█╔ ═┴╟╔▐┼╙╦╔┼ ╧▐╦╔.



■┼╥╬┘╩ ╥┘├┴╥╪ ▐┴╙╘╧ ╧╚╥┴╬╤┼╘ ╫┴╓╬┘┼ ╨╥╧╚╧─┘, ╔ ╫ ╧╙╬╧╫╬╧═ ╧╬ ╬┼ ╫ 
╬┴╙╘╥╧┼╬╔╔ ╨╥╧╨╒╙╦┴╘╪ ≈┴╙. ≡╥┼─▀╤╫╔╘┼ ╚╧╥╧█╔╩ ┴╥╟╒═┼╬╘, ▐╘╧┬┘ "╒┬┼─╔╘╪" ┼╟╧.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.2.2 ∩┬═┼╬╬┘┼ ╦┴═╬╔ 



images/st-swap



∩┬═┼╬╬┘┼ ╦┴═╬╔, ┬╒─╒▐╔ ╒─┴╥┼╬╬┘═╔, ╬┼ ╨╥╧╙╘╧ ╨┼╥┼═┼▌┴└╘╙╤ ╬┴ ╙═┼╓╬┘╩ (╨╒╙╘╧╩) 
╒▐┴╙╘╧╦; ╫═┼╙╘╧ ▄╘╧╟╧, ╧╬╔ ═┼╬╤└╘╙╤ ═┼╙╘┴═╔ ╙ ╦┴═╬┼═ ╦╧╘╧╥┘╩ ╧╬╔ ╒─┴╥╔╠╔. 
≤╠┼─╧╫┴╘┼╠╪╬╧, ┼─╔╬╙╘╫┼╬╬┘╩ ╙╨╧╙╧┬ ╨┼╥┼═┼╙╘╔╘╪ ╧┬═┼╬╬┘╩ ╦┴═┼╬╪ ╔┌ ╧─╬╧╟╧ ═┼╙╘┴ 
╫ ─╥╒╟╧┼--╬┼╧─╬╧╦╥┴╘╬╧ ═┼╬╤╘╪ ┼╟╧ ╙ ─╥╒╟╔═╔ "╧┬┘▐╬┘═╔" ╦┴═╬╤═╔.











[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.2.3 ·┼╥╦┴╠┴ 



images/st-mirrors



∞┴┌┼╥╬┘┼ ╠╒▐╔ ═╧╟╒╘ ╨╥┼╠╧═╠╤╘╪╙╤ ╙ ╨╧═╧▌╪└ ┌┼╥╦┴╠╪╬┘╚ ╦┴═╬┼╩. ≈ Enigma ╙╒▌┼╙╘╫╒┼╘ 
─╫┴ ╘╔╨┴ ┌┼╥╦┴╠╪╬┘╚ ╦┴═╬┼╩: ╨╠╧╙╦╔┼ ┌┼╥╦┴╠┴ ╔ ╘╥┼╒╟╧╠╪╬┘┼ ┌┼╥╦┴╠┴. ≡╠╧╙╦╧┼ ┌┼╥╦┴╠╧ 
╫┼─┼╘ ╙┼┬╤ ╦┴╦ ╧┬┘▐╬╧┼ ┌┼╥╦┴╠╧: ╫╚╧─╤▌╔╩ ╠┴┌┼╥╬┘╩ ╠╒▐ ╧╘╥┴╓┴┼╘╙╤, ┼╙╠╔ ╧╬ 
╨┼╥╨┼╬─╔╦╒╠╤╥┼╬ ┌┼╥╦┴╠╒ ╔ ╧╘╦╠╧╬╤┼╘╙╤ ╫╠┼╫╧ ╔╠╔ ╫╨╥┴╫╧, ┼╙╠╔ ╧╬ ╨┴─┴┼╘ ╬┴ ┌┼╥╦┴╠╧ 
╨╧─ ╒╟╠╧═ ╫ 45 ╟╥┴─╒╙╧╫.



⌠╥┼╒╟╧╠╪╬┘┼ ┌┼╥╦┴╠┴ ╬┼═╬╧╟╧ ╙╠╧╓╬┼┼: ╘╥╔ ╙╘╧╥╧╬┘ ╫┼─╒╘ ╙┼┬╤ ╦┴╦ ╧┬┘▐╬┘┼ ┌┼╥╦┴╠┴, 
╧╘╥┴╓┴╤ ╔ ╧╘╦╠╧╬╤╤ ╫╚╧─╤▌╔╩ ╠╒▐. ε╧ ╠╒▐, ╦╧╘╧╥┘╩ ╨┴─┴┼╘ ╬┴ ╫┼╥█╔╬╒ ╘╥┼╒╟╧╠╪╬╔╦┴ 
╥┴┌─┼╠╤┼╘╙╤ ╬┴ ─╫┴ ╔╙╚╧─╤▌╔╚ ╠╒▐┴, ╦╧╘╧╥┘┼ ─╫╔╓╒╘╙╤ ╫ ╨╥╧╘╔╫╧╨╧╠╧╓╬┘╚ ╬┴╨╥┴╫╠┼╬╔╤╚.



∩┬┴ ╘╔╨┴ ┌┼╥╦┴╠ ─╧╨╧╠╬╔╘┼╠╪╬╧ ═╧╟╒╘ ┬┘╘╪ ╨╧╠╒╨╥╧┌╥┴▐╬┘═╔ ╔╠╔ ╨┼╥┼═┼▌┴┼═┘═╔. 
≡╧╠╒╨╥╧┌╥┴▐╬┘┼ ┌┼╥╦┴╠┴ ╨╥┼╠╧═╠╤└╘ ▐┴╙╘╪ ╫╚╧─╤▌┼╟╧ ╠╒▐┴, ╦┴╦ ╔╚ ╬┼╨╥╧┌╥┴▐╬┘┼ 
┬╥┴╘╪╤, ╬╧ ▐┴╙╘╪ ╠╒▐┴ ╨╥╧╚╧─╔╘ ╬┼╔┌═┼╬╬╧╩. ≡┼╥┼═┼▌┴┼═┘┼ ┌┼╥╦┴╠┴ ╙═╧╬╘╔╥╧╫┴╬┘ 
╬┴ ╙╫┼╘╠╧-╙┼╥┘┼ ╦┴═╬╔, ╬┼╨╧─╫╔╓╬┘┼ ╬┴ ╘┼═╬╧-╙┼╥┘┼ ╦┴═╬╔.



≈┘ ═╧╓┼╘┼ ╨╧╫╧╥┴▐╔╫┴╘╪ ┌┼╥╦┴╠┴, ╙╠┼╟╦┴ ─╧╘╥┴╟╔╫┴╤╙╪ ─╧ ╬╔╚ ╙╫╧╔═ █┴╥╧═. ε╧ ┬╒─╪╘┼ 
╧╙╘╧╥╧╓╬┘ ╙ ┌┼╥╦┴╠┴═╔, ╬┴ ╦╧╘╧╥┘┼ ╒╓┼ ╨┴─┴┼╘ ╠┴┌┼╥╬┘╩ ╠╒▐, ─╧╫╧╠╪╬╧ ╨╥╧╙╘╧ 
╬┼╒═┘█╠┼╬╬╧ ╒╬╔▐╘╧╓╔╘╪ ≈┴█ █┴╥!









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.2.4 ∩─╬╧╙╘╧╥╧╬╬╔┼ ╦┴═╬╔ 



images/st-oneway



■┼╥┼┌ ▄╘╔ ╦┴═╬╔ ═╧╓╬╧ ╨╥╧╩╘╔ ╘╧╠╪╦╧ ╫ ╧─╬╧═ ╬┴╨╥┴╫╠┼╬╔╔. Θ┌ ╬╔╚ ═╧╟╒╘ ┬┘╘╪ ╨╧╙╘╥╧┼╬┘ 
├┼╠┘┼ ╠┴┬╔╥╔╬╘┘, ╬╧ ╫ ╧╙╬╧╫╬╧═ ╧╬╔ ╫┘╬╒╓─┴└╘ ≈┴╙ ┌┴╦╧╬▐╔╘╪ ╧─╬╒ ▐┴╙╘╪ ╒╥╧╫╬╤, ╨┼╥┼─ ╨╥╧╚╧╓─┼╬╔┼═ ╙╠┼─╒└▌┼╩.



⌡ ≈┴╙ ╨╥╧┬╠┼═┘ ╙ ╧─╬╧╙╘╧╥╧╬╬╔═ ╦┴═╬┼═, ╦╧╘╧╥┘╩ ╨╥┼╟╥┴╓─┴┼╘ ≈┴═ ╨╒╘╪? φ╧╓┼╘ ┬┘╘╪ 
╫╧╠█┼┬╬┘╩ ╨╥┼─═┼╘ ╙═╧╓┼╘ ≈┴═ ╨╧═╧▐╪ ....









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.2.5 ≤┼╟╒╬-╦┴═╬╔ 



images/st-shogun



≈ ╬┼╦╧╘╧╥┘╚ ╒╥╧╫╬╤╚ ≈┘ ═╧╓┼╘┼ ╫╙╘╥┼╘╔╘╪ ═╔╟┴└▌╔┼ ╙╔╬╔┼ ╘╧▐╦╔ ╬┴ ╨╧╫┼╥╚╬╧╙╘╔. 
∩╬╔ ═╧╟╒╘ ┬┘╘╪ ┴╦╘╔╫╔╥╧╫┴╬┘ ╨╥┴╫╔╠╪╬╧╩ ╦╧═┬╔╬┴├╔┼╩ ╙┼╟╒╬-╦┴═╬┼╩, ╘╧╟─┴ 
╧╬╔ ╧┬┘▐╬╧ ╙─┼╠┴└╘ ▐╘╧-╘╧ ╨╧╠┼┌╬╧┼, ╬┴╨╧─╧┬╔┼ ╧╘╦╥┘╘╔╤ ─╫┼╥┼╩ ╔╠╔ ╙╧┌─┴╬╔╤ ═╧╙╘╧╫.



φ┴╠┼╬╪╦┴╤ ═╔╟┴└▌┴╤ ╘╧▐╦┴ ┴╦╘╔╫╔╥╒┼╘╙╤ ╨┼╥┼═┼▌┼╬╔┼═ ╬┴ ╬┼┼ ╙┼╟╒╬-╦┴═╬╤ ╙ ═┴╠┼╬╪╦╔═ 
╧╘╫┼╥╙╘╔┼═. ■╘╧┬┘ ┴╦╘╔╫╔╥╧╫┴╘╪ ┬╧╠╪█╔┼ ╘╧▐╦╔, ╧─╬╧╟╧ ╙┼╟╒╬-╦┴═╬╤ ╬┼─╧╙╘┴╘╧▐╬╧. 
≈═┼╙╘╧ ▄╘╧╟╧ ≈┴═ ╬╒╓╬╧ ╨╥┴╫╔╠╪╬╧ ╙╠╧╓╔╘╪ ─╫┴ ╔╠╔ ╘╥╔ ╙┼╟╒╬-╦┴═╬╤, ╫╘┴╠╦╔╫┴╤ ╦┴═╬╔ 
╙ ═┴╠┼╬╪╦╔═╔ ╧╘╫┼╥╙╘╔┼═ ╫ ╦┴═╬╔ ╙ ┬╧╠╪█╔═╔ ╧╘╫┼╥╙╘╔╤═╔. ε┴╨╥╔═┼╥, ┼╙╠╔ ≈┘ ╚╧╘╔╘┼ 
┴╦╘╔╫╔╥╧╫┴╘╪ ╘╧▐╦╒ ╙╥┼─╬┼╟╧ ╥┴┌═┼╥┴, ≈┴═ ╬╒╓╬╧ ╙╬┴▐┴╠┴ ╥┴┌═┼╙╘╔╘╪ ╬┴ ╬┼╩ ╙┼╟╒╬-╦┴═┼╬╪ 
╙ ╧╘╫┼╥╙╘╔┼═ ╙╥┼─╬╔╚ ╥┴┌═┼╥╧╫, ┴ ╨╧╘╧═ ╫╘╧╠╦╬╒╘╪ ╦┴═┼╬╪ ╙ ═┴╠┘═ ╧╘╫┼╥╙╘╔┼═ ╫ ╘╧╘, 
▐╘╧ ┬╧╠╪█┼.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.2.6 Γ╧╠─┼╥┘ 



images/st-bolder



Γ╧╠─┼╥┘ ─╫╔╓╒╘╙╤ ╫ ╬┴╨╥┴╫╠┼╬╔╔, ╨╧╦┴┌┴╬╬╧═ ╬┴ ╬╔╚ ╙╘╥┼╠╦╧╩, ╨╧╦┴ ╬┼ ╙╘╧╠╦╬╒╘╙╤ ╙ 
─╥╒╟╔═ ╦┴═╬┼═. ≈╧┌═╧╓╬╧ ╧╬╔ ┬╠╧╦╔╥╒└╘ ≈┴═ ╨╒╘╪ ╔ ≈┴═ ╬┴─╧ ╧╙╫╧┬╧─╔╘╪ ╔╚ ╘┼═ ╔╠╔ 
╔╬┘═ ╙╨╧╙╧┬╧═. ε╧ ╬╔╦╧╟─┴, ╬╔╦╧╟─┴ ╬┼ ╙╘┴╬╧╫╔╘┼╙╪ ╨┼╥┼─ ╬╔═╔, ╘┴╦ ╦┴╦ ≈┴█ █┴╥ 
═╟╬╧╫┼╬╬╧ ╥┴┌╧┬╪┼╘╙╤, ╦╧╟─┴ ┬╧╠─┼╥ ╨╥╧╩─┼╘ ╨╧ ╬┼═╒!



∩─╬┴╦╧, ≈┘ ╘┴╦╓┼ ═╧╓┼╘┼ ╔╙╨╧╠╪┌╧╫┴╘╪ ╔╚, ╘┴╦ ╦┴╦ ╧╬╔ ╙╨╧╙╧┬╬┘ ╧╘╦╥┘╫┴╘╪ Oxyd-╦┴═╬╔, 
╦╧╟─┴ ╙╘╧╠╦╬╒╘╙╤ ╙ ╬╔═╔. ≈┘ ═╧╓┼╘┼ ╨┼╥┼╬┴╨╥┴╫╔╘╪ ├┼╠┼╬┴╨╥┴╫╠┼╬╬┘┼ ╦┴═╬╔ ╬┼╙╦╧╠╪╦╔═╔ 
╙╨╧╙╧┬┴═╔ ....









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.2.7 δ┴═╬╔-═╧┌┴╔╦╔ 



δ┴═╬╔-═╧┌┴╔╦╔ ╨╧╠╒▐╔╠╔ ╙╫╧┼ ╔═╤ ╔┌-┌┴ ╘╧╟╧, ▐╘╧ ╧╘─┼╠╪╬┘┼ ╦┴═╬╔ ═╧╟╒╘ ┬┘╘╪ ╙╧┼─╔╬┼╬┘ 
╫═┼╙╘┼, ╦┴╦ ╦╒╙╧▐╦╔ ═╧┌┴╔╦╔. ⌡ ╦┴═╬┼╩-═╧┌┴╔╦ ┼╙╘╪ ╥┴┌▀┼═┘ ╬┴ ╬┼╦╧╘╧╥┘╚ ╔╠╔ ╬┴ ╫╙┼╚ 
╙╘╧╥╧╬┴╚, ╦╧╘╧╥┘┼ ═╧╟╒╘ ╨╥╔╦╥┼╨╠╤╘╪╙╤ ╦ ╥┴┌▀┼═┴═ ╙═┼╓╬┘╚ ╦┴═╬┼╩. δ┴╦ ╘╧╠╪╦╧ ╧╬╔ 
┬╒─╒╘ ╙╧┼─╔╬┼╬┘, ╟╥╒╨╨┘ ╦┴═╬┼╩-═╧┌┴╔╦ ╨┼╥┼═┼▌┴└╘╙╤ ╦┴╦ ┼─╔╬╧┼ ├┼╠╧┼. ≈┘ ═╧╓┼╘┼ 
╔╙╨╧╠╪┌╧╫┴╘╪ ▄╘╔ ┬╠╧╦╔, ╬┴╨╥╔═┼╥, ▐╘╧┬┘ ╙╘╥╧╔╘╪ ═╧╙╘┘ ▐┼╥┼┌ ╫╧─╒ ╔╠╔ ┬┼┌─╬╒.



δ╧╟─┴ ╔╚ ╦╧╙╬┼╘╙╤ ╫╧╠█┼┬╬┴╤ ╨┴╠╧▐╦┴, ╦┴═╬╔-═╧┌┴╔╦╔ ╧╘╥┼┴╟╔╥╒└╘ ╨╧ ╥┴┌╬╧═╒. σ╙╠╔ 
┬╠╧╦ ╦┴═╬┼╩-═╧┌┴╔╦ ╙╧┼─╔╬┼╬ ╧╦╧╬▐┴╘┼╠╪╬╧ (─╥╒╟╔═╔ ╙╠╧╫┴═╔ ╒ ╬┼╟╧ ╬┼╘ ╙╫╧┬╧─╬┘╚ 
╥┴┌▀┼═╧╫), ┬╠╧╦ ╬┼═┼─╠┼╬╬╧ ╬┴▐╬┼╘ ╫┌╥┘╫┴╘╪╙╤, ╦┴═┼╬╪ ┌┴ ╦┴═╬┼═. σ╙╠╔ ┬╠╧╦ ╙╧┼─╔╬┼╬ 
╬┼ ─╧ ╦╧╬├┴, ╦┴═╬╔ ╫ ╥╤─╒ ╔╠╔ ╦╧╠╧╬╦┼, ─╧ ╦╧╘╧╥╧╩ ─╧╘╥╧╬╒╠╔╙╪ ╙═┼╙╘╤╘╙╤ ╬┴ ╧─╬╧ 
═┼╙╘╧ ╨╧ ╟╧╥╔┌╧╬╘┴╠╔ ╔╠╔ ╨╧ ╫┼╥╘╔╦┴╠╔.

 

≤╒▌┼╙╘╫╒┼╘ ╥┼─╦╔╩ ╫┴╥╔┴╬╘ ╧┬┘▐╬┘╚ ╦┴═╬┼╩-═╧┌┴╔╦, ╦╧╘╧╥┘╩ ╫┼─┼╘ ╙┼┬╤ ╬┼═╬╧╟╧ ╨╧ 
─╥╒╟╧═╒. ∩╙╬╧╫╬┴╤ ┼╟╧ ╙╥┼─┴ ╧┬╔╘┴╬╔╤ ▄╘╧ ╒╥╧╫╬╔ Oxyd 1, ┴ ╒┌╬┴╘╪ ┼╟╧ ═╧╓╬╧ ╨╧ 
├╫┼╘╒ ╘╥╒┬, ╧╥┴╬╓┼╫╧═╒ ╫═┼╙╘╧ ╙╔╬┼╟╧. ⁿ╘╔ ╦┴═╬╔-═╧┌┴╔╦╔ ╬┼ ═╧╟╒╘ ╨┼╥┼═┼▌┴╘╪╙╤ 
╦┴╦ ┼─╔╬╧┼ ├┼╠╧┼. ∩╬╔ ╫┼─╒╘ ╙┼┬╤ ╦┴╦ ╙╔╬╔┼ ╦┴═╬╔-═╧┌┴╔╦╔, ╦╧╟─┴ ≈┘ ─╧╘╥┴╟╔╫┴┼╘┼╙╪ 
─╧ ╬╔╚ ╫╧╠█┼┬╬╧╩ ╨┴╠╧▐╦╧╩: ┬╠╧╦ ╫┌╥┘╫┴┼╘╙╤, ┼╙╠╔ ╧╬ ╨╧╠╬╧╙╘╪└ ╙╧┼─╔╬┼╬ ╔╠╔ ╥╤─ 
╔╠╔ ╦╧╠╧╬╦┴ ┬╠╧╦┴, ─╧ ╦╧╘╧╥╧╩ ─╧╘╥╧╬╒╠╔╙╪ ╙═┼▌┴┼╘╙╤.  









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 3.2.8 ≡╧▐╘╧╫┘┼ ╦┴═╬╔ 



images/st-mail



≡╧▐╘╧╫┘┼ ╦┴═╬╔ ═╧╟╒╘ ╔╙╨╧╠╪┌╧╫┴╘╪╙╤ ─╠╤ ╨┼╥┼╙┘╠╦╔ ╨╥┼─═┼╘╧╫ ╔┌ ≈┴█┼╟╧ ╔╬╫┼╬╘┴╥╤ 
╫ ╬┼╦╧┼ ╬┼─╧╙╘╒╨╬╧┼ ═┼╙╘╧ ╬┴ ╨╧╫┼╥╚╬╧╙╘╔. δ╧╟─┴ ≈┘ ─╧╘╥┴╟╔╫┴╤╙╪ ╔╙╨╧╠╪┌╒┼╘┼ ╨╧▐╘╧╫┘╩ 
╦┴═┼╬╪, ╨┼╥╫┘╩ ╧┬▀┼╦╘ ╫ ≈┴█┼═ ╔╬╫┼╬╘┴╥┼ ╔┌┘═┴┼╘╙╤ ╔ ╠╧╓╔╘╙╤ ╫ ╦╧╬├┼ ╦┴╬┴╠┴ ╙╫╤┌╔, 
╨╥╔╙╧┼─╔╬┼╬╬╧╟╧ ╦ ╨╧▐╘╧╫╧═╒ ╦┴═╬└. ≈ ┬╧╠╪█╔╬╙╘╫┼ ╙╠╒▐┴┼╫, ≈┘ ─╧╠╓╬┘ ╙┴═╔ ╨╧╙╘╥╧╔╘╪ 
▄╘╧╘ ╦┴╬┴╠, ╬┴╨╥╔═┼╥, "╨┼╥┼╙┘╠┴╤" ╧╘─┼╠╪╬┘┼ ▐┴╙╘╔ ╦┴╬┴╠┴.



Γ╒─╪╘┼ ╧╙╘╧╥╧╓╬┘: ╨╧▐╘╧╫┘╩ ╦┴═┼╬╪ ╬┼ ╥┴┬╧╘┴┼╘, ┼╙╠╔ ╬┴ ╦╧╬├┼ ╦┴╬┴╠┴ ╙╫╤┌╔ ╒╓┼ 
┼╙╘╪ ╧┬▀┼╦╘. ∩▐┼╬╪ ╠┼╟╦╧ ╬┼╒═┘█╠┼╬╬╧ ╨┼╥┼╙╠┴╘╪ ╧┬▀┼╦╘, ╦╧╘╧╥┘╩ ╫╨╧╙╠┼─╙╘╫╔╔ 
┌┴┬╠╧╦╔╥╒┼╘ ╦┴╬┴╠, ╨╧▄╘╧═╒ ┬╒─╪╘┼ ╧╙╘╧╥╧╓╬┘!















[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 4. Σ╧╨╧╠╬╔╘┼╠╪╬┘┼ ╘┼═┘ 





4.1 ≡╧╠╪┌╧╫┴╘┼╠╪╙╦╔┼ ╨┴╦┼╘┘ ╒╥╧╫╬┼╩  Θ╙╘╧╥╔╤, ≥┼┌╒╠╪╘┴╘┘ ╨╧╔╙╦┴ ╔ ß╫╘╧


4.2 ≥┼┌┼╥╫╬╧┼ ╦╧╨╔╥╧╫┴╬╔┼  ■╘╧ ╦╧╨╔╥╧╫┴╘╪ ─╠╤ ┬┼┌╧╨┴╙╬╧╙╘╔


4.3 ≥┼╟╔╙╘╥┴├╔╤ ╧▐╦╧╫  ≡╧┌╫╧╠╪╘┼ ═╔╥╒ ╒┌╬┴╘╪ ╧ ≈┴█┼═ ╒╙╨┼╚┼


4.4 ∩┬╬╧╫╠┼╬╔┼ Enigma               ≤╧╚╥┴╬┼╬╔┼ ╧▐╦╧╫ ╔ ╒╥╧╫╬┼╩ ╨╥╔ ╧┬╬╧╫╠┼╬╔╔












[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 4.1 ≡╧╠╪┌╧╫┴╘┼╠╪╙╦╔┼ ╨┴╦┼╘┘ ╒╥╧╫╬┼╩ 



φ┼╬└ ≡┴╦┼╘ ╒╥╧╫╬┼╩ ╨╥┼─╠┴╟┴┼╘ ╬┼╦╧╘╧╥┘┼ ─╧╨╧╠╬╔╘┼╠╪╬┘┼ ╫╧┌═╧╓╬╧╙╘╔. ≈ ╟╥╒╨╨┼
`User' ┼╙╘╪ ╘╥╔ ╨┴╦┼╘┴ ╒╥╧╫╬┼╩, ╦╧╘╧╥┘┼ ╔┌╬┴▐┴╠╪╬╧ ╨╒╙╘┘:
`Auto Folder', `History' ╔ `Search Result'.



δ╠╔╦┴╤ ╬┴ ╦╬╧╨╦┼ `≡╧╔╙╦' ╫ ═┼╬└ ╨┴╦┼╘╧╫ ╒╥╧╫╬┼╩ ≈┘ ═╧╓┼╘┼ ╔╙╦┴╘╪ ╙╥┼─╔ 
╙╧╫╧╦╒╨╬╧╙╘╔ ╒╥╧╫╬┼╩. ≡╥╧╙╘╧ ╨┼╥┼═┼╙╘╔╘┼ ═┘█╪ ╦ ╘┼╦╙╘╧╫╧═╒ ╨╧╠└ ╔ ╫╫┼─╔╘┼ 
╙╘╥╧╦╒ ─╠╤ ╨╧╔╙╦┴. ≈┘ ═╧╓┼╘┼ ╔╙╦┴╘╪ ╨╧ ┴╫╘╧╥╒, ╬┴┌╫┴╬╔└ ╔ ╔═┼╬╔ ╞┴╩╠┴. ≡╧╔╙╦ ╬┼ 
╫╧╙╨╥╔╔═▐╔╫ ╦ ╥┼╟╔╙╘╥╒. ε┴╨╥╔═┼╥, ≈┘ ═╧╓┼╘┼ ╔╙╦┴╘╪ ╙╘╥╧╦╒ "jump". ≡╧╠╒▐┼╬╬┘┼ 
╒╥╧╫╬╔ ┬╒─╒╘ ╨╥┼─╙╘┴╫╠┼╬┘ ╫ ╨┴╦┼╘┼ ╒╥╧╫╬┼╩ ╨╧─ ╬┴┌╫┴╬╔┼═ "Search Results".



≡┴╦┼╘ ╒╥╧╫╬┼╩ `History' ╧┬╬╧╫╠╤┼╘╙╤ ┴╫╘╧═┴╘╔▐┼╙╦╔ ╙ ╦┴╓─┘═ ╒╥╧╫╬┼═ ╬┴ ╦╧╘╧╥╧═ 
≈┘ ╔╟╥┴╠╔. ⁿ╘╧ ═╧╓┼╘ ╨╥╔╟╧─╔╘╪╙╤, ┼╙╠╔ ≈┘ ╔▌┼╘┼ ╒╥╧╫┼╬╪, ╬┴ ╦╧╘╧╥╧═ ╔╟╥┴╠╔ ╬┴ 
╨╧╙╠┼─╬┼╩ ╬┼─┼╠┼, ╬╧ ╬┼ ┌╬┴┼╘┼ ╦╠└▐┼╫┘╚ ╙╠╧╫ ─╠╤ ╨╧╔╙╦┴.



`Auto Folder' ▄╘╧ ╨┴╦┼╘ ╒╥╧╫╬┼╩, ╦╧╘╧╥┘╩ ≈┘ ═╧╓┼╘┼ ╔╙╨╧╠╪┌╧╫┴╘╪, ▐╘╧┬┘ 
─╧┬┴╫╔╘╪ ╬╧╫┘┼ ╒╥╧╫╬╔, ╬┴╨╥╔═┼╥ ╒╥╧╫╬╔, ╦╧╘╧╥┘┼ ≈┘ ╙╦┴▐┴╠╔ ╔┌ Θ╬╘┼╥╬┼╘┴ ╔╠╔ 
╬┴╨╔╙┴╠╔ ╙┴═╔. ≡┴╨╦┴, ╫ ╦╧╘╧╥╧╩ ≈┘ ─╧╠╓╬┘ ╚╥┴╬╔╘╪ ╒╥╧╫╬╔--`levels/auto' ╫ 
─╔╥┼╦╘╧╥╔╔, ╦╧╘╧╥┴╤ ╒╦┴┌┴╬┴ ╫ ╙╘╥╧╦┼ `≡┴╨╦┴ ╨╧╠╪┌╧╫┴╘┼╠╤' ╫
ε┴╙╘╥╧╩╦╔. δ╧╟─┴ Enigma ┌┴╨╒╙╦┴┼╘╙╤, ╒╥╧╫╬╔ ╫ ▄╘╧╩ ╨┴╨╦┼ ╬┴╚╧─╤╘╙╤ ╔ 
┌┴╟╥╒╓┴└╘╙╤ ┴╫╘╧═┴╘╔▐┼╙╦╔.



Enigma ╨╥┼─╠┴╟┴┼╘ ╬┴═╬╧╟╧ ┬╧╠╪█┼ ╫╧┌═╧╓╬╧╙╘┼╩, ╫┘╚╧─╤▌╔╚ ┌┴ ╨╥┼─┼╠┘ ▄╘╧╟╧ ╥╒╦╧╫╧─╙╘╫┴. 
■╘╧┬┘ ╒┌╬┴╘╪ ╨╧─╥╧┬╬╧╙╘╔, ╨╧╓┴╠╒╩╙╘┴ ╨╥╧▐╘╔╘┼ ╙╨╥┴╫╧▐╬╧┼ ╥╒╦╧╫╧─╙╘╫╧.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 4.2 ≥┼┌┼╥╫╬╧┼ ╦╧╨╔╥╧╫┴╬╔┼ 



σ╙╠╔ ≈┘ ┬╧╔╘┼╙╪ ╨╧╘┼╥╤╘╪ ╫╙┼ ≈┴█╔ ╧▐╦╔, ╫ ╥┼┌╒╠╪╘┴╘┼ ╧╘╦┴┌┴ ╓┼╙╘╦╧╟╧ ─╔╙╦┴, ╔╠╔ 
┼╙╠╔ ≈┘ ╚╧╘╔╘┼ ╨┼╥┼═┼╙╘╔╘╪ ≈┴█╔ ╧▐╦╔ ╙ ╧─╬╧╟╧ ╦╧═╨╪└╘┼╥┴ ╬┴ ─╥╒╟╧╩, ╨╧╠┼┌╬╧ ┌╬┴╘╪, 
╦┴╦ ┌┴╥┼┌┼╥╫╔╥╧╫┴╘╪ ╔╬╞╧╥═┴├╔└ ╧ ╙╧╙╘╧╤╬╔╔ Enigma. ■╘╧┬┘ ╙─┼╠┴╘╪ ▄╘╧, ╙╬┴▐┴╠┴ 
╬┴╩─╔╘┼ ╫ ε┴╙╘╥╧╩╦╔ Enigma
`≡┴╨╦╒ ╨╧╠╪┌╧╫┴╘┼╠╤'.  ≈┘ ═╧╓┼╘┼ ╨╥╧╙╘╧ ╙─┼╠┴╘╪ ╥┼┌┼╥╫╬╒└ ╦╧╨╔└ ╘╧╩ ╨┴╨╦╔
--╫┴╓╬┘═╔ ╤╫╠╤└╘╙╤ ╞┴╩╠┘ `enigma.score' ╔ `state.xml'.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 4.3 ≥┼╟╔╙╘╥┴├╔╤ ╧▐╦╧╫ 



Σ╠╤ ╥┼╟╔╙╘╥┴├╔╔ ≈┴█╔╚ ╧▐╦╧╫, ≈┴═ ╬╒╓╬╧ ╧╘╨╥┴╫╔╘╪ ╬┴═ ╞┴╩╠ `enigma.score', 
╥┴╙╨╧╠╧╓┼╬╬┘╩ ╫ ─╔╥┼╦╘╧╥╔╔ `≡┴╨╦┴ ╨╧╠╪┌╧╫┴╘┼╠╤'. ≡╧╓┴╠╒╩╙╘┴ ╔▌╔╘┼ ┬╧╠┼┼ 
╨╧─╥╧┬╬┘┼ ╒╦┴┌┴╬╔╤ ╬┴ ─╧═┴█╬┼╩ ╙╘╥┴╬╔├┼ ╨╥╧┼╦╘┴.



■╘╧┬┘ ┴╫╘╧═┴╘╔▐┼╙╦╔ ╙╦┴▐╔╫┴╘╪ ╙╨╔╙╦╔ ╧┬╬╧╫╠┼╬╬┘╚ ═╔╥╧╫┘╚ ╥┼╦╧╥─╧╫, ≈┴═ ╨╥╧╙╘╧ 
╬╒╓╬╧ ╫╦╠└▐╔╘╪ ╧╨├╔└ `∩┬╬╧╫╠╤╘╪ ╥┼╩╘╔╬╟'.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 4.4 ∩┬╬╧╫╠┼╬╔┼ Enigma 



σ╙╠╔ ≈┘ ╬┼ ╬┴╙╘╥┴╔╫┴╠╔ ≈┴█╒ ╙╘┴╥╒└ ╫┼╥╙╔└, ╨╥╧╙╘╧ ╒─┴╠╔╘┼ ╙╘┴╥╒└ ╫┼╥╙╔└ ╔ ╒╙╘┴╬╧╫╔╘┼ 
╬╧╫╒└. ⁿ╘╧ ╫╙┼, ▐╘╧ ≈┘ ─╧╠╓╬┘ ╙─┼╠┴╘╪, ╘┴╦ ╦┴╦ ≈┴█╔ ╧▐╦╔ ┴╫╘╧═┴╘╔▐┼╙╦╔ ╧┬╬╧╫╤╘╙╤.



σ╙╠╔ ≈┴═ ╨╧╬┴─╧┬╔╘╙╤ ─╧┬┴╫╔╘╪ ╒╥╧╫╬╔ ╫ ─╔╥┼╦╘╧╥╔╔ ╒╙╘┴╬╧╫╦╔ Enigma, ≈┴═ ╬╒╓╬╧ 
╙─┼╠┴╘╪ ╔╚ ╥┼┌┼╥╫╬╒└ ╦╧╨╔└ ╨┼╥┼─ ╒─┴╠┼╬╔┼═. ≡╧╙╠┼ ▄╘╧╟╧ ≈┘ ═╧╓┼╘┼ ┬┼┌ ╧╨┴╙┼╬╔╩ 
╒─┴╠╔╘╪ ╙╘┴╥╒└ ╫┼╥╙╔└ ╔ ╒╙╘┴╬╧╫╔╘╪ ╬╧╫╒└.



≤╘┴╥┘╩ ╞┴╩╠ ╧▐╦╧╫ `~/.enigmarc2' ─╠╤ ╙╔╙╘┼═ ╙ ╨┼╥┼═┼╬╬╧╩ ╧╦╥╒╓┼╬╔╤ `HOME' 
╔╠╔ `.../Application Data/enigmarc.lua2' ─╠╤ ╠╔█┼╬╬┘╚ "HOME" ╙╔╙╘┼═ Windows 
┴╫╘╧═┴╘╔▐┼╙╦╔ ╨╥┼╧┬╥┴┌╒┼╘╙╤ ╫ ╬╧╫┘╩ ╞╧╥═┴╘. ≈┘ ═╧╓┼╘┼ ╒─┴╠╔╘╪ ╙╘┴╥┘┼ ╧▐╦╔ ╨╧╙╠┼ 
╨┼╥╫╧╟╧ ╒╙╨┼█╬╧╟╧ ┌┴╨╒╙╦┴ Enigma 1.00.



σ╙╠╔ ≈┘ ╚╧╘╔╘┼ ╔╟╥┴╘╪ ╬┴ ╒╥╧╫╬╤╚, ╦╧╘╧╥┘┼ ≈┘ ╙╧╚╥┴╬╔╠╔ ╙╧ ╙╘┴╥╧╩ ╒╙╘┴╬╧╫╦╔, 
╨╧╓┴╠╒╩╙╘┴ ╨╥╧▐╘╔╘┼ ╙╨╥┴╫╧▐╬╧┼ ╥╒╦╧╫╧─╙╘╫╧.









[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 5. ≤╨╧╩╠┼╥┘ 



ⁿ╘╧╘ ╥┴┌─┼╠ ╙╧─┼╥╓╔╘ ╨╧─╙╦┴┌╦╔ ─╠╤ ╬┼╦╧╘╧╥┘╚ ╙╠╧╓╬┘╚ ╒╥╧╫╬┼╩. ε┴╙╘╧╤╘┼╠╪╬╧ ╬┼ 
╥┼╦╧═┼╬─╒┼╘╙╤ ▐╔╘┴╘╪ ╙╨╧╩╠┼╥┘, ┼╙╠╔ ≈┘ ╬┼ ┌┴╙╘╥╤╠╔ ╧╦╧╬▐┴╘┼╠╪╬╧. ε┼╦╧╘╧╥┘┼ ╒╥╧╫╬╔ 
╬┴═┼╥┼╬╬╧ ╒╙╠╧╓╬┼╬┘ ╔ ─┴╓┼ ╔╟╥╧╦┴═-╫┼╘┼╥┴╬┴═ Enigma ╬╒╓╬┘ ▐┴╙┘, ▐╘╧┬┘ ╥┼█╔╘╪ ╔╚. 
ε┼╦╧╘╧╥┘┼ ╒╥╧╫╬╔ ╠┼╟▐┼ ╥┼█╔╘╪ ╫ ╒╨╥╧▌┼╬╬╧═ ╥┼╓╔═┼ ╔╟╥┘ (╙═╧╘╥╔╘┼ (see section φ┼╬└ ╒╥╧╫╬┼╩).





5.1 ≡╥╧╚╧╓─┼╬╔┼ Advanced Tutorial  


5.2 ≤╧╫┼╘┘ ─╠╤ ╬┼╙╦╧╠╪╦╔╚ ╒╥╧╫╬┼╩  











[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 5.1 ≡╥╧╚╧╓─┼╬╔┼ Advanced Tutorial 



≤▐╔╘┴┼╘╙╤, ▐╘╧ ═┼╙╘╬╧╙╘╔ ╫ ╨┴╦┼╘┼ ╒╥╧╫╬┼╩ "Tutorial" ╨╥╧╙╘┘. δ╥╧═┼ ╨╧╙╠┼─╬┼╩, 
╦╧╘╧╥┴╤ ╬┼ ╘┴╦ ╨╥╧╙╘┴ ....  ⁿ╘╧╘ ╥┴┌─┼╠ ╥╒╦╧╫╧─╙╘╫┴ ╨╥┼─╧╙╘┴╫╠┼╬ Jacob Scott.



ⁿ╘╧ ╨╥╧╚╧╓─┼╬╔┼ ═╧┼╟╧ ╒╥╧╫╬╤ "Advanced Tutorial" ╫ ╨┴╦┼╘┼ ╒╥╧╫╬┼╩ "Tutorial" 
(▐╘╧┬┘ ═┼╬╤╘╪ ╨┴╦┼╘┘ ╒╥╧╫╬┼╩, ╦╠╔╦╬╔╘┼ ╬┴ "≡┴╦┼╘ ╒╥╧╫╬┼╩" ╫╬╔┌╒-╙╠┼╫┴ ▄╦╥┴╬┴ ╔ 
╫┘┬┼╥╔╘┼ ╨┴╦┼╘ ╒╥╧╫╬┼╩). ≈╧ ╫╥┼═╤ ╔╟╥┘ ╫ ╨┼╥╫╒└ ╧▐┼╥┼─╪, ≈┴═ ╬╒╓╬╧ ▐╔╘┴╘╪ ╫╙┼ 
─╧╦╒═┼╬╘┘ ╫ ╦╧═╬┴╘┼.



δ╧╬┼▐╬┴╤ ├┼╠╪ ▄╘╧╟╧ ╒╥╧╫╬╤, ╦┴╦ ╔ ┬╧╠╪█╔╬╙╘╫┴ ╒╥╧╫╬┼╩ Enigma, ╬┴╩╘╔ ╔ ─╧╘╥╧╬╒╘╪╙╤ 
─╧ ╫╙┼╚ "Oxyd-╦┴═╬┼╩" ╙╫╧╔═ ▐┼╥╬┘═ █┴╥╔╦╧═. δ╧╟─┴ ≈┘ ╦┴╙┴┼╘┼╙╪ Oxyd-╦┴═╬╤, ╧╬ 
╧╘╦╥┘╫┴┼╘╙╤ ╔ ╨╧╦┴┌┘╫┴┼╘ ├╫┼╘. σ╙╠╔ ≈┘ ─╧╘╥╧╬┼╘┼╙╪ ╨╧ ╧▐┼╥┼─╔ ─╧ ─╫╒╚ Oxyd-╦┴═╬┼╩ 
╧─╔╬┴╦╧╫╧╟╧ ├╫┼╘┴, ╧╬╔ ╧┬┴ ╧╙╘┴╬╒╘╙╤ ╧╘╦╥┘╘┘═╔. ≈┘ ┌┴╫┼╥█╔╘┼ ╒╥╧╫┼╬╪, ╦┴╦ ╘╧╠╪╦╧ 
╨╧─┬┼╥┼╘┼ ╫╙┼ ╨┴╥┘ Oxyd-╦┴═╬┼╩ ╬┴ ╒╥╧╫╬┼.



≈ ╒╥╧╫╬┼ ╧╦╧╠╧ ─╫┴─├┴╘╔ ╦╧═╬┴╘, ╙╧┬╥┴╬╬┘╚ ╫ ╘╥╔ ╧╘─┼╠╪╬┘╚ ╧┬╠┴╙╘╔. ≈ ╨┼╥╫╧╩ ╧┬╠┴╙╘╔ 
≈┘ ╫╙╘╥┼╘╔╘┼ ╬┼╦╧╘╧╥┘┼ ╧╙╬╧╫╬┘┼ ╘╔╨┘ ┬╠╧╦╧╫ ╔ ╨╧╫┼╥╚╬╧╙╘┼╩, ╦╧╘╧╥┘┼ ╫╙╘╥┼▐┴└╘╙╤ 
╫ Enigma ╔ ╥┼█╔╘┼ ╨┴╥╒ ╨╥╧╙╘┘╚ ╟╧╠╧╫╧╠╧═╧╦. ≈╘╧╥┴╤ ╧┬╠┴╙╘╪ ╙╠╧╓╬┼┼ ╔ ╨╧┌╬┴╦╧═╔╘ 
≈┴╙ ╙ ╨╧╠┼┌╬┘═╔ ╨╥╔┼═┴═╔ ╧┬═┴╬┴ ┴╦╘╔╫╬╧╟╧ ╫╥┴╟┴. ⌠╥┼╘╪╤ ╔ ╨╧╙╠┼─╬╤╤ ╧┬╠┴╙╘╪ ─┴╙╘ 
≈┴═ ╨╧▄╦╙╨┼╥╔═┼╬╘╔╥╧╫┴╘╪ ╙ ╨╥╧─╫╔╬╒╘┘═ ╫┌┴╔═╧─┼╩╙╘╫╔┼═ ═┼╓─╒ ╧┬▀┼╦╘┴═╔ Enigma. ≈ 
▄╘╧═ ╧╘─┼╠╪╬╧═ ╒╥╧╫╬┼, ╫╙┼╫╧┌═╧╓╬┘┼ ╦┴═╬╔ ═╧╟╒╘ ┬┘╘╪ ╬┴╩─┼╬┘ ╫ ╧─╬╧╩ ╦╧═╬┴╘┼ ╫ 
╦╧╬├┼ ╘╥┼╘╪┼╩ ╧┬╠┴╙╘╔.








[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 5.1.1 ∩┬╠┴╙╘╪ 1 



≈┘ ╬┴▐╔╬┴┼╘┼ ╫ ╦╧═╬┴╘┼ ╧╦╥╒╓┼╬╬╧╩ ╬┼╨╧─╫╔╓╬┘═╔ ╙╘┼╬┴═╔, ╦╥╧═┼ ╨╥╧╚╧─┴ ╙╨╥┴╫┴, 
╫╧─┘ ╫╬╔┌╒-╙╠┼╫┴ ╔ ┌┴╦╥┘╘╧╟╧ ╨╥╧╚╧─┴ ╫╫┼╥╚╒-╙╨╥┴╫┴.



δ╧═╬┴╘┴ 1: Θ─╔╘┼ ▐┼╥┼┌ ╨╥╧╚╧─ ╫ ╙╘┼╬┼ ╙╨╥┴╫┴.



δ╧═╬┴╘┴ 2: ≡╥╧╙╘╧ ╔┌┬┼╟┴╩╘┼ ┬╠╧╦╧╫ ╙ ╔┌╧┬╥┴╓┼╬╬┘═ ╬┴ ╬╔╚ ▐┼╥┼╨╧═.



δ╧═╬┴╘┴ 3: ≤╘╧╠╦╬╔╘┼ ▐┼╘┘╥┼ ─┼╥┼╫╤╬╬┘╚ ╤▌╔╦┴ ╫ ╫╧─╒ ╫ ╥╤─, ▐╘╧┬┘ ╙╧┌─┴╘╪ ═╧╙╘ 
╬┴ ╨╥╧╘╔╫╧╨╧╠╧╓╬┘╩ ┬┼╥┼╟. ⌠┼╨┼╥╪ ╘╧╠╦╬╔╘┼ ▐┼╥╬╧╫┴╘┘┼ ┬╠╧╦╔ ╙╨╥┴╫┴. ≡┼╥┼─╫╔╬╪╘┼ 
┬╠╧╦╔ ╔┌ ╦╧╥┘ ╙ ╨╒╘╔ (╫╧┌═╧╓╬╧ ╫╠┼╫╧) ╔ ╨╧╙╘╥╧╩╘┼ ═╧╙╘ ╙╨╥┴╫┴ ╔┌ ─┼╥┼╫╤╬╬┘╚ ╤▌╔╦╧╫.



δ╧═╬┴╘┴ 4: ≡╧─╧╩─╔╘┼ ╨╧┬╠╔╓┼ ╦ ╫╧╠▐╦╒. δ╧╟─┴ ╧╬ ╨╧╟╧╬╔╘╙╤ ┌┴ ≈┴═╔, ╫┼─╔╘┼ ┼╟╧ 
╫╠┼╫╧ ╔ ╫╧╦╥╒╟ ┬╠╧╦╧╫ ╫ ├┼╬╘╥┼ ╦╧═╬┴╘┘. δ┴╦ ╘╧╠╪╦╧ ╫╧╠▐╧╦ ┬╒─┼╘ ─┴╠┼╦╧ ╧╘ ╨┼╥┼╚╧─┴ 
╬┴ ╙╠┼─╒└▌╔╩ ╒╥╧╫┼╬╪, ╨╥╧╙╦╧▐╔╘┼ ╘╒─┴.



δ╧═╬┴╘┴ 5: σ─╔╬╙╘╫┼╬╬┴╤ ╧╨┴╙╬╧╙╘╪ ┌─┼╙╪--▐┼╥┼╨┴ ╫╬╔┌╒ ╦╧═╬┴╘┘. ≡┼╥╫┘╩ ╘╔╨ 
╨╧╫┼╥╚╬╧╙╘╔ ▄╘╧ ═┼╘┴╠╠--▄╘┴ ╨╧╫┼╥╚╬╧╙╘╪ ╨╧╚╧╓┴ ╬┴ "╠╔╙╘╫┼╬╬╒└", ╨╧ ╦╧╘╧╥╧╩ ≈┘ 
╨┼╥┼─╫╔╟┴╠╔╙╪ ╥┴╬┼┼. ≤╠┼─╒└▌┴╤ ╨╧╫┼╥╚╬╧╙╘╪ "╦╥┴╙╬┴╤"--╬┴ ▄╘╧╩ ╨╧╫┼╥╚╬╧╙╘╔ ╙╠╧╓╬╧ 
┌┴═┼─╠╔╘╪╙╤ ╔╠╔ ╒╙╦╧╥╔╘╪╙╤. ⌠╥┼╘╔╩ ╘╔╨ ▄╘╧ ╠┼─--╬┴ ▄╘╧╩ ╨╧╫┼╥╚╬╧╙╘╔ ╙╠┴┬╧┼ ╘╥┼╬╔┼. 
≡╧╙╠┼─╬╔╩ ╘╔╨ ╨╧╫┼╥╚╬╧╙╘╔ ▄╘╧ ╦╧╙═╧╙--┌─┼╙╪ ╫╧╧┬▌┼ ╬┼╘ ╘╥┼╬╔╤; ╫┘ ╬┼ ═╧╓┼╘┼ ╔┌═┼╬╔╘╪ 
╫┼╦╘╧╥ ╙╦╧╥╧╙╘╔ (╙╦╧╥╧╙╘╪ ╔ ╬┴╨╥┴╫╠┼╬╔┼), ╦╧╟─┴ ≈┘ ╬┴╚╧─╔╘┼╙╪ ╬┴ ▄╘╧╩ ╨╧╫┼╥╚╬╧╙╘╔.



δ╧═╬┴╘┴ 6: ≡╥╧╙╘╧ ╔─╔╘┼ ╨╧ ╙╦╠╧╬┴═. ≡╧╘╧═ ╫┘╩─╔╘┼ ╫╠┼╫╧, ╨╥╧╩─╤ ╨╧ "╧┬╥┴╘╬╧╩" 
╨╧╫┼╥╚╬╧╙╘╔--╦╧╟─┴ ╬┴ ▄╘╧╩ ╨╧╫┼╥╚╬╧╙╘╔ ≈┘ ╬┴╨╥┴╫╠╤┼╘┼ ═┘█╪ (╔╠╔ ╨╧╚╧╓╔╩ ╦╧╬╘╥╧╠╠┼╥) 
╫ ╧─╬╧═ ╬┴╨╥┴╫╠┼╬╔╔, █┴╥ ╒╙╦╧╥╤┼╘╙╤ ╫ ╧┬╥┴╘╬╧═ (┼╙╠╔ ╒ ≈┴╙ ╙ ▄╘╔═ ╨╥╧┬╠┼═┘, 
╨╧╨╥╧┬╒╩╘┼ ╨╧╫┼╥╬╒╘╪ ≈┴█╒ ═┘█╪ ╬┴ 180 ╟╥┴─╒╙╧╫).



δ╧═╬┴╘┴ 7: ≡╧╨┘╘┴╩╘┼╙╪ ╨╧╠╒▐╔╘╪ ─╧╨╧╠╬╔╘┼╠╪╬┘╩ █┴╥, ╨╧╙╘┴╫╔╫ ╨╧─╫╔╓╬┘╩ ┬╠╧╦ ╬┴ 
╬╔╓╬╔╩ ╨┼╥┼╦╠└▐┴╘┼╠╪. ≤╬┴▐┴╠┴ ╘╧╠╦╬╔╘┼ ┼╟╧ ╬┴ ╧─╔╬ ╦╫┴─╥┴╘ ╫╫┼╥╚, ╨╧╘╧═ ╫╠┼╫╧ 
╬┴ █┼╙╘╪ ╦╫┴─╥┴╘╧╫. ≡╧╘╧═ ╘╧╠╦╬╔╘┼ ┼╟╧ ╬┴ ╨╤╘╪ ╦╫┴─╥┴╘╧╫ ╫╬╔┌ ╔ ─╫┴ ╫╨╥┴╫╧. ≈ 
╦╧╬├┼ ╦╧╬├╧╫ ╘╧╠╦╬╔╘┼ ┼╟╧ ╬┴ ╧─╔╬ ╦╫┴─╥┴╘ ╫╫┼╥╚ ╔ ╧─╔╬ ╫╠┼╫╧. ≈╧┌╪═╔╘┼ ─╧╨╧╠╬╔╘┼╠╪╬┘╩ 
█┴╥ ╔ ┌┴╘┼═ ╨╧╙╘┴╫╪╘┼ ┬╠╧╦ ╬┴ ─╥╒╟╧╩ ╨┼╥┼╦╠└▐┴╘┼╠╪, ▐╘╧┬┘ ╧╘╦╥┘╘╪ ╨╥╧╚╧─ ╙╠┼╫┴ 
╧╘ ╦╧═╬┴╘┘.



δ╧═╬┴╘┴ 8: ≈╧┌╪═╔╘┼ ─╔╬┴═╔╘ (≈┴═ ╬╒╓╬╧ ┬╒─┼╘ ┌┴╩╘╔ ╬┴ ╠┼─) ╔ ┬╥╧╙╪╘┼ ┼╟╧ ╬┴╨╥╧╘╔╫ 
╓┼╠╘┘╚ ┬╠╧╦╧╫, ▐╘╧┬┘ ╫┌╧╥╫┴╘╪ ╔╚ ╔ ╨╥╧╩╘╔. ∞╧╨┴╘┴ ╬┼ ╧┬╤┌┴╘┼╠╪╬┴, ╬╧ ╧╙╘┴╬╪╘┼╙╪ 
╨╧▄╦╙╨┼╥╔═┼╬╘╔╥╧╫┴╘╪ ╙ ╬┼╩.



δ╧═╬┴╘┴ 9: ⌠╧╠╦╬╔╘┼ ╙┴═┘╩ ╬╔╓╬╔╩ ╨╧─╫╔╓╬┘╩ ┬╠╧╦ ╫╠┼╫╧. ≤┼╩▐┴╙ ┬╧╠─┼╥┘, ╨┘╘┴└▌╔┼╙╤ 
╨╥╧╩╘╔ ╫╨╥┴╫╧, ╨╥┼╟╥┴╓─┴└╘ ≈┴═ ╨╒╘╪. ⌠╧╠╦╬╔╘┼ ╙┴═┘╩ ╨╥┴╫┘╩ ╨╧─╫╔╓╬┘╩ ┬╠╧╦ (╫╠┼╫╧ 
╔╠╔ ╫╨╥┴╫╧), ▐╘╧┬┘ ─┴╘╪ ╙╨╧╠┌╘╔ ┬╧╠─┼╥┴═. ≈╧┌╪═╔╘┼ ╫╧╠█┼┬╬╒└ ╨┴╠╧▐╦╒ (╬┼ ─╧╘╥┴╟╔╫┴╩╘┼╙╪ 
╙╠╒▐┴╩╬╧ ╬╔ ─╧ ╦┴╦╔╚ ╨╧─╫╔╓╬┘╚ ┬╠╧╦╧╫, ╦╧╟─┴ ╫╧╠█┼┬╬┴╤ ╨┴╠╧▐╦┴ ╬┴╚╧─╔╘╙╤ ╫ ╬┴▐┴╠┼ 
≈┴█┼╟╧ ╔╬╫┼╬╘┴╥╤) ╔ ╘╧╠╦╬╔╘┼ ╨╧─╫╔╓╬┘╩ ┬╠╧╦ ╬┴─ ╫╧─╧╩ ╫╬╔┌. ⌠┼╨┼╥╪ ╫┼╥╬╔╘┼╙╪ ╫ 
╨╥┴╫╒└ ▐┴╙╘╪ ╦╧═╬┴╘┘, ╫┘╙╘┴╫╪╘┼ ╫╧╠█┼┬╬╒└ ╨┴╠╧▐╦╒ ╫ ╬┴▐┴╠╧ ≈┴█┼╟╧ ╔╬╫┼╬╘┴╥╤ ╔ 
╦╧╙╬╔╘┼╙╪ ╘╥┼╚ ╫┼╥╚╬╔╚ ┬╧╠─┼╥╧╫ ╔┌ ─╠╔╬╬╧╟╧ ╙╘╧╠┬├┴ (╨╧╙╘┴╥┴╩╘┼╙╪ ╬┼ ╨╧╨┴─┴╘╪╙╤ 
╬┴ ╨╒╘╔ ╠└┬┘╚ ┬╧╠─┼╥╧╫). ⌠╧╠╦╬╔╘┼ ╙┴═┘╩ ╠┼╫┘╩ ╨╧─╫╔╓╬┘╩ ┬╠╧╦ ╫╠┼╫╧ ╔ ╔─╔╘┼ ╫ 
╙╠┼─╒└▌╒└ ╦╧═╬┴╘╒.



δ╧═╬┴╘┴ 10: δ╧╙╬╔╘┼╙╪ ╨┼╥┼╦╠└▐┴╘┼╠╤. ⌠┼╨┼╥╪ ╘╧╠╦╬╔╘┼ ─╫┴ ┬╠╧╦┴ ╔┌ ╦╧╥┘ ╫╫┼╥╚ (╬┴ 
╧─╔╬ ╦╫┴─╥┴╘ ╦┴╓─┘╩). ⌠╧╠╦╬╔╘┼ ╙╥┼─╬╔╩ (╙╫┼╥╚╒ ╫╬╔┌) ─┼╥┼╫╤╬╬┘╩ ╤▌╔╦ ╫╠┼╫╧, ┴ 
─┼╥┼╫╤╬╬┘╩ ╤▌╔╦, ╙╨╥┴╫┴-╙╫┼╥╚╒ ╧╘ ╬┼╟╧ ╫ ╫╧─╒. ≤╘╧╠╦╬╔╘┼ ╧╙╘┴╫█╔┼╙╤ ╤▌╔╦╔ ╫ ╫╧─╒, 
▐╘╧┬┘ ╧┬╥┴┌╧╫┴╘╪ ╙╘╧╠┬┼├ (╨╧╙╘┴╥┴╩╘┼╙╪ ╬┼ ╒╘╧╬╒╘╪). ⌠┼╨┼╥╪ ╒─┴╥╪╘┼ ╧╦╬╧ (╟╧╠╒┬╒└ 
╨╧╠╧╙╒) ╬┴ ┬╧╠╪█╧╩ ╙╦╧╥╧╙╘╔. ≈╧┌╪═╔╘┼ █┴╥ ╔ ╨┼╥┼╩─╔╘┼ ▐┼╥┼┌ ═╧╙╘ ╫ ╨┼╥╫╒└ ╦╧═╬┴╘╒. 
∩╘╙└─┴ ╔─╔╘┼ ╫ ╧╘╦╥┘╫█╔╩╙╤ ╨╥╧╚╧─.








[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 5.1.2 ∩┬╠┴╙╘╪ 2 



≈╧ ╫╘╧╥╧╩ ╧┬╠┴╙╘╔ ≈┘ ╫╙╘╥┼╘╔╘┼ ╥╧╘╧╥, ╤╫╠╤└▌╔╩╙╤ ┴╦╘╔╫╬┘═ ╨╥╧╘╔╫╬╔╦╧═ ≈┴█┼╟╧ 
▐┼╥╬╧╟╧ █┴╥┴. ≥┴┌╠╔▐╬┘┼ ╥╧╘╧╥┘ ═╧╟╒╘ ─┼╩╙╘╫╧╫┴╘╪ ╬┼╙╦╧╠╪╦╧ ╥┴┌╠╔▐╬╧, ╬╧ ╧╬╔ 
╫╙┼╟─┴ ╬┼╨╧╬╤╘╠╔╫┘. ≡╥┼─╬┴┌╬┴▐┼╬╔┼ ╨╧╙╠┼─╬┼╟╧--┌┴╙╘┴╫╔╘╪ ┼╟╧ ╙─┼╠┴╘╪, ╘╧ ▐╘╧ 
≈┴═ ╬╒╓╬╧, ─┼╥╓┴╙╪ ╬┴ ┬┼┌╧╨┴╙╬╧═ ╥┴╙╙╘╧╤╬╔╔.



∩╙═╧╘╥╔╘┼╙╪ ╫ ▄╘╧╩ ╧┬╠┴╙╘╔ (╬╧ ╨╧╦┴ ╬┼ ╘╥╧╟┴╩╘┼ ╨╧─╫╔╓╬┘╩ ┬╠╧╦). ≈┴═ ╬╒╓╬╧ 
╨╥╧╩╘╔ ▐┼╥┼┌ ╘╥╧┼ ┌┴╦╥┘╘┘╚ ╫╧╥╧╘ ╫ ╫┼╥╚╒ ▄╘╧╩ ╧┬╠┴╙╘╔.



≡┼╥╫┘┼ ╫╧╥╧╘┴: ⌠╧╠╦╬╔╘┼ ┬┼╠┘╩ █┴╥ ╫╠┼╫╧ (╬┼ ╨╥╧╩─╔╘┼ ╙╠╒▐┴╩╬╧ ▐┼╥┼┌ ▐┼╥╬┘╩ 
╧─╬╧╙╘╧╥╧╬╬╔╩ ┬╠╧╦) ▐╘╧┬┘ ╧╙╫╧┬╧─╔╘╪ ┼╟╧ (▄╘╧ ═╧╓┼╘ ╨╧╘╥┼┬╧╫┴╘╪ ╬┼╙╦╧╠╪╦╔╚ 
╨╧╨┘╘╧╦). ≈╧┌╪═╔╘┼ ╠╧╓╦╒ ╔ ─╧╫╧╠╪╬╧ ╙╔╠╪╬╧ ╘╧╠╦╬╔╘┼ ┬┼╠┘╩ █┴╥ ▐┼╥┼┌ ┬┼╠┘╩ 
╧─╬╧╙╘╧╥╧╬╬╔╩ ┬╠╧╦, ▐╘╧┬┘ ╧╬ ╬┼ ╧╙╘┴╬╧╫╔╠╙╤. ⌠┼╨┼╥╪ ╔─╔╘┼ ▐┼╥┼┌ ▐┼╥╬┘╩ ╧─╬╧╙╘╧╥╧╬╬╔╩ 
┬╠╧╦ ╔ ╨╥╧╫┼─╔╘┼ ┬┼╠┘╩ █┴╥ ▐┼╥┼┌ ╨╥╧╚╧─. Σ╧╫╧╠╪╬╧ ╙╔╠╪╬╧ ╘╧╠╦╬╔╘┼ ┬┼╠┘╩ █┴╥ ▐┼╥┼┌ 
╙╠┼─╒└▌╔╩ ┬┼╠┘╩ ╧─╬╧╙╘╧╥╧╬╬╔╩ ┬╠╧╦, ▐╘╧┬┘ ╧╬ ╬┼ ╧╙╘┴╬╧╫╔╠╙╤ ╬╔╓┼. δ┴╦ ╘╧╠╪╦╧ ┬┼╠┘╩ 
█┴╥ ╨╥╧╩─┼╘, ╔╙╨╧╠╪┌╒╩╘┼ ╠╧╓╦╒; ≈┘ ╫╬╧╫╪ ╬┴▐╬┼╘┼ ╒╥╧╫┼╬╪ ╫ ╬┴▐┴╠┼ ╔ ┬╧╠╪█┼ ╬╔▐┼╟╧ 
╬┼ ╙╠╒▐╔╘╙╤. ≤╬╧╫┴ ╨╥╧╩─╔╘┼ ▐┼╥┼┌ ╫╧╥╧╘┴--╨┼╥╫┘┼ ╫╧╥╧╘┴ ╫╫┼╥╚╒ ╦╧═╬┴╘┘ ╧╘╦╥┘╘┘.



≈╘╧╥┘┼ ╫╧╥╧╘┴: ⌠╧╠╦╬╔╘┼ ╨╧─╫╔╓╬┘╩ ┬╠╧╦ ╫ ╙┴═╧╩ ╨╥┴╫╧╩ ╦╧═╬┴╘┼ ▄╘╧╩ ╧┬╠┴╙╘╔ ╫╨╥┴╫╧ 
╔ ┬┼╟╔╘┼. ≈ ╫╧╥╧╘┴╚, ╙╧┼─╔╬╤└▌╔╚ ╫╘╧╥╒└ ╔ ╘╥┼╘╪└ ╧┬╠┴╙╘╪, ╨╧╤╫╔╘╙╤ ─╧╦╒═┼╬╘ ╙ 
╨╧╠┼┌╬╧╩ ╔╬╞╧╥═┴├╔┼╩. ≡╧─╫┼─╔╘┼ ╥╧╘╧╥ (┌┴╙╘┴╫╠╤╤ ┼╟╧ ╟╬┴╘╪╙╤ ┌┴ ≈┴═╔, ╦┴╦ ≈┘ 
─┼╠┴╠╔ ▄╘╧ ╙ ╫╧╠▐╦╧═) ╦ ╬╔┌╒ ╙╘┼╬┘ ╙╨╥┴╫┴ ╧╘ ╫╧╥╧╘ ═┼╓─╒ ╨┼╥╫╧╩ ╔ ╫╘╧╥╧╩ ╧┬╠┴╙╘╤═╔. 
≡╥╧╩─╔╘┼ ▐┼╥┼┌ ╫╧╥╧╘┴ ╔ ▐┼╥┼┌ ═╧╙╘ ╫ ╦╧═╬┴╘╒ ╨╧─ ≈┴═╔. δ╧╙╬╔╘┼╙╪ ╨┼╥┼╦╠└▐┴╘┼╠╤, 
▐╘╧┬┘ ┌┴╦╥┘╘╪ ╫╧╥╧╘┴ ╔ ╫┼╥╬╔╘┼╙╪ ╫ ╦╧═╬┴╘╒ ╧╘╦╒─┴ ≈┘ ╬┴▐┴╠╔. ≈┘ ┬╧╠╪█┼ ╬┼ ╫╔─╔╘┼ 
╥╧╘╧╥--┼╟╧ ╬┼ ┬╒─┼╘ ╫ ╘╧╩ ╦╧═╬┴╘┼, ╟─┼ ╔ ≈┘--╬╧ ┼╙╠╔ ╨╥╔╙═╧╘╥┼╘╪╙╤, ≈┘ ╙═╧╓┼╘┼ 
╒╫╔─┼╘╪ ╟─┼ ╧╬. π┼╠╪ ┌─┼╙╪ ╙╧╙╘╧╔╘ ╫ ╘╧═, ▐╘╧┬┘ ╬┼ ╨╧─╫┼╥╟┴╤ ╙┼┬╤ ╧╨┴╙╬╧╙╘╔, ┌┴╙╘┴╫╔╘╪ 
╥╧╘╧╥ ╨╧╩╘╔ ╦ ╨┼╥┼╦╠└▐┴╘┼╠└ ╔ ╧╘╦╥┘╘╪ ─╠╤ ≈┴╙ ─╫┼╥╪. ≡╒╙╘╪ ╥╧╘╧╥ ╨╧╩─┼╘ ┌┴ ≈┴═╔ ╔┌ 
╫┼╥╚╬┼╟╧-╨╥┴╫╧╟╧ ╒╟╠┴ ▄╘╧╩ ╦╧═╬┴╘┘ ╫ ╫┼╥╚╬╔╩-╠┼╫┘╩. ∩╬ ─╧╠╓┼╬ ┬┘╘╪ ╫┘╘╧╠╦╬╒╘ ╫╠┼╫╧ 
╬┼╙╦╧╠╪╦╔═╔ ╬┴╦╠╧╬┴═╔. Σ╧╫┼─╔╘┼ ╥╧╘╧╥ ╫╬╔┌ ╙╠┼╫┴, ╨╧╦┴ ╧╬ ╬┼ ╨╥╧─╧╠╓╔╘ ╙╫╧╩ ╨╒╘╪ ╔ 
≈┘ ╬┼ ╒╙╠┘█╔╘┼ ┌╫╒╦ ╬┴╓┴╘╧╟╧ ╨┼╥┼╦╠└▐┴╘┼╠╤. δ╧╙╬╔╘┼╙╪ ╨┼╥┼╦╠└▐┴╘┼╠╤, ▐╘╧┬┘ ╧╘╦╥┘╘╪ 
╫╧╥╧╘┴ ╔ ╫┼╥╬╒╘╪╙╤ ╫╧ ╫╘╧╥╒└ ╧┬╠┴╙╘╪ ? ╫╘╧╥┘┼ ╫╧╥╧╘┴, ─╧╠╓╬┘ ┬┘╘╪ ╧╘╦╥┘╘┘.



⌠╥┼╘╪╔ ╫╧╥╧╘┴: ≡╥╧╙╘╧ ╘╧╠╦╬╔╘┼ ╨╧─╫╔╓╬┘╩ ┬╠╧╦, ╔┌ ╦╧╘╧╥╧╟╧ ╫┘╙╦╧▐╔╠ ╥╧╘╧╥, ╬┴ 
╨┼╥┼╦╠└▐┴╘┼╠╪ ╫ ╦╧═╬┴╘┼, ╟─┼ ╧╬ ╨╧╤╫╔╠╙╤. ≈┼╥╬╔╘┼╙╪ ╫ ╦╧═╬┴╘╒ ╙╠┼╫┴ ╧╘ ≈┴╙--╘╥┼╘╪╔ 
╫╧╥╧╘┴ ─╧╠╓╬┘ ┬┘╘╪ ╧╘╦╥┘╘┘. Θ─╔╘┼ ▐┼╥┼┌ ╘╥╧┼ ╧╘╥┘╘┘╚ ╫╧╥╧╘.








[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 5.1.3 ∩┬╠┴╙╘╪ 3 



≈ ╘╥┼╘╪┼╩ ╧┬╠┴╙╘╔ ≈┴═ ╬╒╓╬╧ ╔╙╙╠┼─╧╫┴╘╪ ╫┌┴╔═╧─┼╩╙╘╫╔╤ ═┼╓─╒ ╥┴┌╠╔▐╬┘═╔ ╧┬▀┼╦╘┴═╔ 
Enigma. ·─┼╙╪ ≈┘ ╬┴╩─┼╘┼ ╠┴┌┼╥┘, ┌┼╥╦┴╠┴ ╔ ═╧╬┼╘┘. ≈┴═ ╨╥╔╩─┼╘╙╤ ╥┼█╔╘╪ ╨╥╧╙╘╒└ 
╟╧╠╧╫╧╠╧═╦╒ ╠┴┌┼╥-╔-┌┼╥╦┴╠╧, ▐╘╧┬┘ ─┴╘╪ ╠┴┌┼╥╒ ╨╧╨┴╙╘╪ ╫ ╧╘─┼╠╪╬┘╩ ╦┴═┼╬╪, ╦╧╘╧╥┘╩ 
╧╘╦╥╧┼╘ ═╧╙╘ ╫ ╙╠┼─╒└▌╒└ ╦╧═╬┴╘╒. ■╘╧┬┘ ╨╥┼╧─╧╠┼╘╪ ╙╠┼─╒└▌╔┼ ╬┼╙╦╧╠╪╦╧ ╦╧═╬┴╘, 
≈┘ ─╧╠╓╬┘ ╙╧┌─┴╘╪ ╬┼╙╦╧╠╪╦╧ ╬╧╫┘╚ ╧┬▀┼╦╘╧╫, ╨╥╧╓╔╟┴╤ ╠┴┌┼╥╬┘═ ╠╒▐╧═ ╙╒▌┼╙╘╫╒└▌╔┼ 
╧┬▀┼╦╘┘.



≈ ╨┼╥╫╧╩ ▐┴╙╘╔ ▄╘╧╩ ╧┬╠┴╙╘╔ ┼╙╘╪ ╘╥╔ ┌┼╥╦┴╠┴ ╔ ╠┴┌┼╥ ╙ ╨┼╥┼╦╠└▐┴╘┼╠┼═.



δ╧═╬┴╘┴ 1: ≈┴═ ╬╒╓╬╧ ─┴╘╪ ╠┴┌┼╥╒ ╨╧╨┴╙╘╪ ╫ ▐┼╥╬┘╩ ╦┴═┼╬╪. ⌠╧╠╦╬╔╘┼ ╬╔╓╬┼┼-╠┼╫╧┼ 
┌┼╥╦┴╠╧ ╬┴ ╧─╔╬ ╦╫┴─╥┴╘ ╫╬╔┌ ╔ ╨╧╫┼╥╬╔╘┼ ┼╟╧ ╘┴╦, ▐╘╧┬┘ ╧╬╧ ╫┘╟╠╤─┼╠╧ ╬┴╨╧─╧┬╔┼ 
"\" ╠┼╟╦╧ ─╧╘╥┴╟╔╫┴╤╙╪ ─╧ ╬┼╟╧ (╫╠┼╫╧ ╫╨╠╧╘╪ ─╧ ╠┴┌┼╥┴ ─╧╠╓╬╧ ┬┘╘╪ ╘╥╔─├┴╘╪ 
╦╫┴─╥┴╘╧╫). ⌠╧╠╦╬╔╘┼ ╫┼╥╚╬┼┼-╠┼╫╧┼ ┌┼╥╦┴╠╧ ╬┴ ╫╧╙┼═╪ ╦╫┴─╥┴╘╧╫ ╫╠┼╫╧, ╬┴ ╧─╔╬ 
╦╫┴─╥┴╘ ╫╬╔┌ ╔ ╨╧╫┼╥╬╔╘┼ ┼╟╧, ▐╘╧┬┘ ╧╬╧ ┬┘╠╧ ╨╧╚╧╓┼ ╬┴ "/" (╧╬╧ ─╧╠╓╬╧ ┬┘╘╪ ╫ 
▐┼╘┘╥┼╚ ╦╫┴─╥┴╘┴╚ ╧╘ ╨╥┼─┘─╒▌┼╟╧ ┌┼╥╦┴╠┴ ╔ ╨╥╤═╧ ╬┴─ ╬╔═). ⌠╧╠╦╬╔╘┼ ╫┼╥╚╬┼┼-╨╥┴╫╧┼ 
┌┼╥╦┴╠╧ ╬┴ ─╫┴ ╦╫┴─╥┴╘┴ ╫╫┼╥╚, ┴ ┌┴╘┼═ ╬┴ ╘╥╔ ╦╫┴─╥┴╘┴ ╫╨╥┴╫╧ (╧╬╧ ─╧╠╓╬╧ ┬┘╘╪ 
╨╥┴╫┼┼ ╬┴ ─╫┴─├┴╘╪ ─╫┴ ╦╫┴─╥┴╘┴ ╧╘ ╨╥┼─┘─╒▌┼╟╧ ┌┼╥╦┴╠┴ ╔ ╬┴ ╧─╔╬ ╦╫┴─╥┴╘ ╬╔╓┼ 
▐┼╥╬╧╟╧ ╦┴═╬╤). ≥┴╙╨╧╠╧╓╔╘┼ ▄╘╧ ┌┼╥╦┴╠╧ ╫ ╫╔─┼ "/". ⌠┼╨┼╥╪ ─╧╘╥╧╬╪╘┼╙╪ ─╧ ╨┼╥┼╦╠└▐┴╘┼╠╤, 
▐╘╧┬┘ ╫╦╠└▐╔╘╪ ╠┴┌┼╥ (╬┼ ╨╧╨┴─╔╘┼ ╨╧─ ╬┼╟╧ ╔╠╔ ╬┼ ╨╥╧╚╧─╔╘┼ ▐┼╥┼┌ ╠┴┌┼╥╬┘╩ ╠╒▐). 
δ┴╦ ╘╧╠╪╦╧ ▄╘╧ ┬╒─┼╘ ╙─┼╠┴╬╧, ╔─╔╘┼ ▐┼╥┼┌ ═╧╙╘ ╙╨╥┴╫┴ ╧╘ ≈┴╙.



δ╧═╬┴╘┴ 2: ≈╧┌╪═╔╘┼ ╬┼╙╦╧╠╪╦╧ ═╧╬┼╘ ╔ ╫╧┌╫╥┴▌┴╩╘┼╙╪ ╫ ╨╥┼─┘─╒▌╒└ ╦╧═╬┴╘╒. ≈┘╦╠└▐╔╫ 
╔ ╫╦╠└▐╔╫ ╠┴┌┼╥, ╨╧╥┴┌╔╘┼ ╠┴┌┼╥╬┘═ ╠╒▐╧═ ╧─╬╒ ╔┌ ═╧╬┼╘. ≈╧┌╪═╔╘┼ ╨╧╠╒▐┼╬╬┘╩ ╧┬▀┼╦╘ 
(┌╧╬╘), ╨╧╫╘╧╥╔╘┼ ╨╥╧├┼╙╙ ╔ ╫╧┌╪═╔╘┼ ╫╘╧╥╧╩ ┌╧╬╘. ⌠┼╨┼╥╪ ┬╥╧╙╪╘┼ ╧─╬╒ ╔┌ ═╧╬┼╘ ┌┴ 
┌┼╥╦┴╠╧═ ╔ ╙─╫╔╬╪╘┼ ╬┴ ╬┼┼ ┌┼╥╦┴╠╧. ≡╧╥┴┌╔╘┼ ▄╘╒ ═╧╬┼╘╒ ╙╧ ┌╬┴▐┼╬╔┼═ ╨╤╘╪ ╠┴┌┼╥╧═, 
▐╘╧┬┘ ╙╧┌─┴╘╪ ═╧╠╧╘. ≡╧╥┴┌╔╘┼ ╠┴┌┼╥╧═ ═╧╠╧╘ (╫┘╦╠└▐╔╫ ╔ ╫╦╠└▐╔╫ ╠┴┌┼╥), ▐╘╧┬┘ ╙╧┌─┴╘╪ 
═┼▐. σ╙╠╔ ≈┘ ╚╧╘╔╘┼ ╬┼╙╦╧╠╪╦╧ ─╧╨╧╠╬╔╘┼╠╪╬┘╚ █┴╥╧╫, ≈┘ ═╧╓┼╘┼ ╨┼╥┼╘┴▌╔╘╪ ┌┼╥╦┴╠╧ ╬┴─ 
═╧╬┼╘╧╩ ─╫┴╓─┘ ╔ ╨╧╥┴┌╔╘╪ ╠┴┌┼╥╧═ ═╧╬┼╘╒ ╙ ╒╫┼╠╔▐┼╬╬┘═ ┌╬┴▐┼╬╔┼═ (╙┴═╧┼ ┬╧╠╪█┼┼, 
─╧ ─┼╙╤╘╔). ■╘╧┬┘ ╫┼╥╬╒╘╪╙╤ ╫ ╦╧═╬┴╘╒ ╙ ╥┘├┴╥╤═╔, ╨╧╙╘┴╫╪╘┼ ┌┼╥╦┴╠┴ ╫ ╔╚ ╬┴▐┴╠╪╬┘┼ 
╨╧┌╔├╔╔, ╒┬┼╥╔╘┼ ╫╙┼ ╧┬▀┼╦╘┘, ┬╠╧╦╔╥╒└▌╔┼ ╠┴┌┼╥ ╔ ╦╧╙╬╔╘┼╙╪ ╨┼╥┼╦╠└▐┴╘┼╠╤. ⌠┼╨┼╥╪ 
╔╙╨╧╠╪┌╒╤ ╨╥┴╫╒└ ╦╬╧╨╦╒ ═┘█╔ ╔╠╔ ╦╠┴╫╔█╒ "Tab" ╫┘╙╘┴╫╪╘┼ ╫ ╬┴▐┴╠╧ (╙╠┼╫┴) ╙╫╧┼╟╧ 
╔╬╫┼╬╘┴╥╤ ═┼▐. ⌡─┴╥╪╘┼ ╬┼╙╦╧╠╪╦╧ ╥┘├┴╥┼╩ (╦┴╓─╧╟╧ ╨╧ ▐┼╘┘╥┼ ╥┴┌┴), ▐╘╧┬┘ ╨╥╧╩╘╔.



δ╧═╬┴╘┴ 3: Θ╙╨╧╠╪┌╒╩╘┼ ┌╧╬╘ ╔ ╨╥╧╙╠┼─╒╩╘┼ ╬┴─ ┬┼┌─╬╧╩ ╫ ╦╧═╬┴╘╒ ╨╧─ ≈┴═╔, ┴ 
┌┴╘┼═ ╫ ╦╧═╬┴╘╒ ╙╨╥┴╫┴ ╧╘ ≈┴╙. σ╙╠╔ ╧╦╥╒╓┴└▌┼┼ ≈┴╙ ╦╧╠╪├╧ ╬┴▐╬┼╘ ═╔╟┴╘╪, 
╔╙╨╧╠╪┌╒╩╘┼ ─╥╒╟╧╩ ┌╧╬╘.



δ╧═╬┴╘┴ 4: ≡╥╧╙╘╧ ╨╧─┬┼╥╔╘┼ ╨┴╥┘ Oxyd-╦┴═╬┼╩ ─╧╘╥┴╟╔╫┴╤╙╪ ─╧ Oxyd-╦┴═╬┼╩ 
╧─╔╬┴╦╧╫╧╟╧ ├╫┼╘┴ ╙ ┴╦╘╔╫╔╥╧╫┴╬╬┘═╔ Oxyd-╦┴═╬╤═╔ (╨╧ ╧─╬╧═╒ ┌┴ ╥┴┌). ε┼ ╘╥╧╟┴╩╘┼ 
╟╥╒┬┘┼ ╦┴═╬╔ (▐┼╥╬┘┼ ╦┴═╬╔). ≈┘ ╫┘╔╟╥┴╠╔!










[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 5.2 ≤╧╫┼╘┘ ─╠╤ ╬┼╙╦╧╠╪╦╔╚ ╒╥╧╫╬┼╩ 





 I/6: Welcome to the Machine


≤╧╧┬▌┼╬╔┼ ╫┬╠╔┌╔ ╫┼╥╚╬┼╟╧-╨╥┴╫╧╟╧ ╒╟╠┴ ╙╧─┼╥╓╔╘ ╫┴╓╬┘╩ ╙╧╫┼╘.





 I/8: Easy?


≡╧╙╘┴╫╪╘┼ ╨┼╥╫┘╩ ╙┼╟╒╬-╦┴═┼╬╪ ╫ ╫┼╥╚╬╔╩ ╠┼╫┘╩ ╒╟╧╠, ┴ ╫╘╧╥╧╩ ╬┴─ ╙┴═╧╩ 
╨╥┴╫╧╩ ╙┼╟╒╬-╘╧▐╦╧╩.





 I/31: Where Am I?


Θ╙╨╧╠╪┌╒╩╘┼ ─┼╥┼╫╤╬╬┘┼ ╤▌╔╦╔, ▐╘╧┬┘ ╬┼ ┌┴┬╠╒─╔╘╪╙╤. 





 I/32: The Grim Reaper


≈╙┼╟─┴ ╠╔ ≈┘ ╙▐╔╘┴┼╘┼, ▐╘╧ ≈┴█┴ ═┘█╪ ╨┼╥┼╫┼╥╬╒╘┴???





 I/43: Sokoban Revival


≡╧═╬╔╘┼? ⁿ╘╧ ╨┼╥╫┘╩ ╒╥╧╫┼╬╪ ╧╥╔╟╔╬┴╠╪╬╧╟╧ ≤╧╦╧┬┴╬┴ …  ∩╬ ╫┼─╪ ╬┼ ╘┴╦╧╩ ╘╥╒─╬┘╩!





 I/65: Lasers 101


≡╧╙╘┴╫╪╘┼ ─╫┴ ┌┼╥╦┴╠┴ ╫╫┼╥╚╒ ╔ ╧─╬╧ ╫╬╔┌╒. ≡┼╥┼═┼▌┴╤ ┌┼╥╦┴╠┴ ╔ ╘╧▐╬╧ ├┼╠╤╙╪, 
≈┘ ═╧╓┼╘┼ ╨╧╨┴╙╘╪ ╠┴┌┼╥╬┘═ ╠╒▐╧═ ╨╧ ╫╙┼═ Oxyd-╦┴═╬╤═.





 I/72: Way to Go


∩─╬┴ ╔┌ ╙╔╬╔╚ ╘╧▐┼╦ ╫┼─┼╘ ╙┼┬╤ ╨╧-╥┴┌╬╧═╒. ≈╧╙╨╧╠╪┌╒╩╘┼╙╪ ▄╘╔═!





 I/80: Meditation


≥┴╙╨╧╠╧╓╔╘┼ █┴╥╔╦╔ ╟╧╥╔┌╧╬╘┴╠╪╬╧. 





 II/15: Knock Knock!


≡╧╙╘╒▐╔╘┼╙╪ ╫ ╙╘┼╬┘.





 II/27: Twelve doors


≈┘ ╧╘╦╥┘╠╔ ╫╙┼ ─╫┼╥╔ ╔ ╫╙┼ ╥┴╫╬╧ ╬┼ ═╧╓┼╘┼ ╨╥╧╩╘╔? ≈┘ ▐╘╧-╘╧ ╨╥╧╨╒╙╘╔╠╔!





 II/40: Space Meditation


≤╠┘█┴╠╔ ╦╧╟─┴-╬╔┬╒─╪ ╧ ╨╥╧┬╠┼═┼ ╘╥┼╚ ╘┼╠?





 II/44: Pharaos' Tombs


∩┬╥┴╘╔╘┼╙╪ ╦ "Easy Shifting ....".





 II/56: Easy Shifting ....


∩┬╥┴╘╔╘┼╙╪ ╦ "Running Rings".





 II/57: Floppy Swapping


≡┼╥╫╧┼--╬┴╩─╔╘┼ ─╔╙╦┼╘╒ ╔ ╫╧╠█┼┬╬╒└ ╨┴╠╧▐╦╒, ╧╬╔ ≈┴═ ╨╧╬┴─╧┬╤╘╙╤. ≈╘╧╥╧┼--╫╙┼╟─┴
╬╧╙╔╘┼ ─╔╙╦┼╘╒ ╔ ╫╧╠█┼┬╬╒└ ╨┴╠╧▐╦╒ ╙ ╙╧┬╧╩. ⌠╥┼╘╪┼--╬┼╦╧╘╧╥┘┼ ╦┴═╬╔ ╨╧╚╧╓╔, ╬╧ 
─┼╩╙╘╫╒└╘ ╬┼ ╧─╔╬┴╦╧╫╧.





 II/59: The Disappearing Block


·┴╓═╔╘┼ ╠┴┌┼╥.





 II/65: Laser Magic


≈╥┼═╤ ╒┌╬┴╘╪ ╬┼╙╦╧╠╪╦╧ ╫┼▌┼╩ ╧ ╨╥┼╧┬╥┴┌╧╫┴╬╔╔ ╧┬▀┼╦╘╧╫. ⁿ╦╙╨┼╥╔═┼╬╘╔╥╒╩╘┼!





 II/69: Question of Speed


Θ╠╔ ╙╦╧╥┼┼: ≈╧╨╥╧╙ ╬┴▐┴╠┴???  





 II/77: Push Your Way


≤╬┴▐┴╠┴ ╬┴╩─╔╘┼ ╫╧╠█┼┬╬╒└ ╨┴╠╧▐╦╒! 





 II/97: Tool Time


≡╥╤▐╪╘┼ ╧╨┴╙╬┘┼ ╔╬╙╘╥╒═┼╬╘┘ ╧╘ ─┼╘┼╩.





 II/99: Domain of Mysteries


∩╙╘╧╥╧╓╬╧ ╨╥╧─╫╔╟┴╩╘┼╙╪ ╦ ╒╙╨┼╚╒.





 II/100: Patterns


σ╙╘╪ ╠╔ ┌─┼╙╪ ╨╧─╧┬╔┼?





 III/14: Use the PIN


.... ╔╠╔ ╫╧╙╨╧╠╪┌╒╩╘┼╙╪ ≈┴█┼╩ ╠└┬╔═╧╩ ▄╬├╔╦╠╧╨┼─╔┼╩, ┼╙╠╔ ≈┘ ╬┼ ═╧╓┼╘┼ ╘╧▐╬╧ 
╫╙╨╧═╬╔╘╪ ▐╔╙╠╧.





 III/16: Control Panel


≤╧╧┬▌┼╬╔┼ ╫ ╠┼╫╧╩ ╦╧═╬┴╘┼ ╥┴╙╙╦┴╓┼╘ ≈┴═, ╦┴╦ ╥┴╙╨╧╠╧╓╔╘╪ ┬╠╧╦╔ ╫ ╨┼╥╫╧╩ ╙╘╥╧╦┼ 
╨┼╥┼╦╠└▐┴╘┼╠┼╩. ≡╧╙╠┼ ▄╘╧╟╧, ╔╙╨╧╠╪┌╒╩╘┼ ╦╧─┘ ├╫┼╘╧╫, ╨╧╦┴┌┴╬╬┘╚ ╫ ╠┼╫╧╩ ╦╧═╬┴╘┼. 





 III/22: Portable Laser


Γ╒─╪╘┼ ╨╥╔┌╬┴╘┼╠╪╬┘!





 III/27: Tricks and Traps


ε┼ ═╧╓┼╘┼ ╫┘┬╥┴╘╪╙╤ ╔┌ ╨┼╥╫╧╟╧ ▄╦╥┴╬┴? ≤╦╧╬├┼╬╘╥╔╥╒╩╘┼╙╪ ╙╬┴▐┴╠┴ ╬┴ ═╔╟┴└▌┼╩ ╘╧▐╦┼. 
ε┼ ═╧╓┼╘┼ ╬┴╩╘╔ ╨╧╙╠┼─╬╔╩ Oxyd-╦┴═┼╬╪? ß╦╘╔╫╔╥╒╩╘┼ ╘╥╔ ╔┌ ┬╧╠╪█╔╚ ═╔╟┴└▌╔╚ ╘╧▐┼╦ 
╬┴ ╨┼╥╫╧═ ▄╦╥┴╬┼ ╔ ═┴╠┼╬╪╦╔╩ ╬┴ ╘╥┼╘╪┼═ ▄╦╥┴╬┼.





 III/28: Wells


Γ╧╔╘┼╙╪ ╒═┼╥┼╘╪?





 III/29: Push? Pull!


∩─╬┴ ╨┼╥┼╙╘┴╬╧╫╦┴ ╫╫┼╥╚ - ∩─╬┴ ╨┼╥┼╙╘┴╬╧╫╦┴ ╫╬╔┌ - τ╧╠╧╫╧╠╧═╦┴ ╫╨╥┴╫╧ - ≡╥╧─╧╠╓╔╘┼ ─┴╠╪█┼!





 III/40: Snow White


⌠╥╔ ═┴╠┼╬╪╦╔╚ ▄╙╦╔═╧╙┴ - ≤╫╤┌┴╬╬┘┼ ╫ ╦╧╠╪├╧ ╬┴ ╠┼─╤╬╧═ ╨╧╠┼ - ε┼ ═╧╟╒╘ ╬┴╩╘╔ ╔╚ ═┴╠┼╬╪╦╔┼ ╔╟╠╒ - ≤╦╥┘╘┘┼ ╨╧─ ╙╬┼╓╬┘═ ╨╧╦╥╧╫╧═.





 III/43: The Ditch


≈┘ ╬┼ ═╧╓┼╘┼ ╥┼█╔╘╪ ▄╘╧╘ ╒╥╧╫┼╬╪ ┬┼┌ ╨╧╘┼╥╔ ╙╫╧┼╟╧ "±".





 III/49: What's the Problem?


∞╧╫╒█╦╔ ╨╧ ╫╙┼╩ ╘┼╥╥╔╘╧╥╔╔ … ▄╘╧ ═┼╙╘╬╧╙╘╪ ─╠╤ ═┼─╔╘┴├╔╔.





 III/95: Jump and Run


σ╙╘╪ ╨╥╒╓╔╬┴, ╙╨╥╤╘┴╬╬┴╤ ┌┴ ┌┼╥╦┴╠╧═.





 IV/6: TNT Shortage?


≤ ═╧╠╧╘╦╧═ ╨╥╧▌┼!





 IV/17: Flood Gates


∩╙╘╧╥╧╓╬╧┼ ┌┴╘╧╨╠┼╬╔┼ ╧╨╥┼─┼╠┼╬╬┘╚ ╧┬╠┴╙╘┼╩ ═╧╓┼╘ ╨╥╔╟╧─╔╘╪╙╤. ε┼ ╨╧╦╔─┴╩╘┼ ╨┼╥╫╒└ 
╦╧═╬┴╘╒ ┬┼┌ ┴╦╘╔╫┴├╔╔ ╬╔╓╬┼╟╧ ╨┼╥┼╦╠└▐┴╘┼╠╤. φ╬╧╟╔┼ ╔┌ ╫╙┼╚ ╬╔╓╬╔╚ ╨┼╥┼╦╠└▐┴╘┼╠┼╩ 
─┼╩╙╘╫╒└╘ ╧─╔╬┴╦╧╫╧.





 IV/25: Light Switches


·┴╓═╔╘┼ ╠┴┌┼╥┘, ┼╙╠╔ ≈┘ ╬┼ ─╧╙╘┴╘╧▐╬╧ ┬┘╙╘╥┘. 





 IV/27: Robbery


≡╥╧┬┼╥╔╘┼╙╪ ╫ ┬┴╬╦, ▐┼╥┼┌ ╘╥┼▌╔╬┘ ╫ ╨╧╠╒. 





 IV/34: Running Rings


∩┬╥┴╘╔╘┼╙╪ ╦ "Pharao's Tomb".





 IV/39: How Many Spirals?


ε┼╦╧╘╧╥┘┼ ╠└─╔ ╫┘╨╥┘╟╔╫┴└╘ ╔┌ ╧╦╬┴ ╨╥╔ ╨╧╓┴╥┼  - ╨╧╙╘╒╨╔╘┼ ╔╬┴▐┼.





 IV/47: Just Moving Blocks?


≤╠╔█╦╧═ ═╬╧╟╧ ─┼╥┼╫╤╬╬┘╚ ╤▌╔╦╧╫? δ┴╦ ┬┘ ≈┴═ ╒┬╥┴╘╪ ╧─╔╬?





 IV/48: Artillery


≡╒█┼▐╬╧┼ ╤─╥╧ ╘╧╓┼ ╧╘╦╥┘╫┴┼╘ Oxyd-╦┴═╬╔.





 IV/54: Fire Safety


≡┼╥┼╦╠└▐┴╘┼╠╪ ╫╥┼─╔╘ ≈┴═? ⌡╬╔▐╘╧╓╪╘┼ ┼╟╧!





 IV/64: The Flagstone Reaper


ⁿ╘╧ ╫┘╨╧╠╬╤┼╘╙╤.





 IV/65: Little Bit of Everything


ε┴╩─╔╘┼ ╙╨╧╙╧┬ ╒╬╔▐╘╧╓┼╬╔╤.





 V/15: Solvable?


ε┼ ╬┴╨╧═╔╬┴┼╘ ╠╔ ≈┴═ ╧ ▐┼═-╘╧ ·≤α≈?





 V/16: Draggers


≡╥╔╬╤╘╧ ╙▐╔╘┴╘╪, ▐╘╧ ▄╘╧╘ ╒╥╧╫┼╬╪--┌╠╧. ≤╒▌┼╙╘╫╒┼╘ ╔╙╘╧▐╬╔╦, ╙╨╥╤╘┴╬╬┘╩ ╫╧┌╠┼ 
≈┴█┼╟╧ ╬┴▐┴╠╪╬╧╟╧ ╨╧╠╧╓┼╬╔╤.





 V/24: Space Pirates


ⁿ╘╧╘ ╒╥╧╫┼╬╪ ╚╔╘╥┘╩. ≡╧─╧╓╟╔╘┼ ┬╧═┬╒ ╫╧┌╠┼ ─┼╥┼╫╤╬╬┘╚ ╤▌╔╦╧╫.





 V/32: Walk the Plank


ε┼ ╚╫┴╘┴┼╘ ╨╔╥┴╘╧╫, ▐╘╧┬┘ ╨╧╦╧╥╔╘╪ ▄╘╧╘ ╒╥╧╫┼╬╪? σ╙╘╪ ─╥╒╟╧╩, ┬╧╠┼┼ ╨╥╧╙╘╧╩ ╨╒╘╪.





 V/34: Island of Safety


ε┴▐╬╔╘┼ ┴╬┴╠╔┌ ╙ ╙╧╘╬╔.





 V/45: Psycho Pushing


⌠╧╠╦┴╩ ╔ ┬┼╟╔.





 V/58: Now What?


δ╧╟─┴ ≈┘ ╫╔─╔╘┼ ╨┼╥┼╙┼▐┼╬╔┼, ▐╘╧ ─╧╠╓╬╧ ┬┘╘╪ ╫ ╙╠┼─╒└▌┼═ ╥╤─╒?





 V/78: Don't Be Greedy


τ─┼-╘╧ ╫ ▄╘╧═ ╥╒╦╧╫╧─╙╘╫┼ ┼╙╘╪ ╙╧╫┼╘ ╨╧╠╒▐█┼.





 V/89: Ice-Bomb


≡╧─ ╦┴═╬┼═ ╙╨╥╤╘┴╬ ╠╒▐█╔╩ ╙╧╫┼╘.





 V/91: Firefox


≡╧╠ ╟╧╥╔╘ ┬┘╙╘╥┼┼.





 VI/8: Orbitting


ε┼ ╨╧┌╫╧╠╤╩╘┼ ╬╔▐┼═╒ ─╧╘╥┴╟╔╫┴╘╪╙╤ ─╧ ╟╥┴╬╔├.





 VI/23: Prepare Your Defense


∞┴┌┼╥ ╔┌═┼╬╤┼╘ ╬┼ ╘╧╠╪╦╧ ╨╥┼─═┼╘┘.





 esprit 43


≡╥╔╬┼╙╔╘┼ ╓┼╥╘╫╒ ╫╒╠╦┴╬╒.





 esprit 52


Θ╟╥┴╩╘┼ ─╧ ╨╧╥┘ ─╧ ╫╥┼═┼╬╔.





 esprit 100


≈┌╧╥╫╔╘┼ ╒╟╧╠.





 Oxyd Magnum 99 (level 22): Letter Bomb


≡╧─╧╥╫╔╘┼ ╫┌╥┘╫┴└▌╔┼╙╤ ╦┴═╬╔.





 PerOxyd 49 (level 22): Hidden Treasure


⌡─╧╙╘╧╫┼╥╪╘┼╙╪, ▐╘╧ ╒ ≈┴╙ ╫╙┼╟─┴ ┼╙╘╪ ─╧╙╘╒╨ ╦ ╦╧═╬┴╘┼ ╙ ╨┼╥┼╦╠└▐┴╘┼╠┼═ ╬┴ ╨╧╠╒. ≡╧╘╧═ ╔▌╔╘┼ ╫╘╧╥╧╩ ▄╦╥┴╬ ╙╧ "╙╨╥╤╘┴╬╬┘═╔ ╙╧╦╥╧╫╔▌┴═╔".














[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 6. Γ╠┴╟╧─┴╥╬╧╙╘╔ 





6.1 τ╠┴╫╬┘┼ ╥┴┌╥┴┬╧╘▐╔╦╔  


6.2 ∩╙╧┬┘┼ ┬╠┴╟╧─┴╥╬╧╙╘╔  


6.3 ≡╧═╧▌╬╔╦╔  


6.4 Θ╙╨╧╠╪┌╒┼═╧┼ ╨╥╧╟╥┴══╬╧┼ ╧┬┼╙╨┼▐┼╬╔┼  












[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 6.1 τ╠┴╫╬┘┼ ╥┴┌╥┴┬╧╘▐╔╦╔ 





 Raoul Bourquin


≥╒╦╧╫╧─╙╘╫╧ ╒╥╧╫╬╤═╔ ╔ ─╔┌┴╩╬, ┬┼╙├┼╬╬┘┼ ─╧╨╧╠╬┼╬╔╤ ╨╧ ╫╙┼═ ╫╧╨╥╧╙┴═





 Siegfried Fennig


Σ╔┌┴╩╬ ╒╥╧╫╬┼╩, ╟╥┴╞╔╦┴





 Martin Hawlisch


Σ╔┌┴╩╬ ╒╥╧╫╬┼╩, ╟╥┴╞╔╦┴, ╨╥╧╟╥┴══╔╥╧╫┴╬╔┼





 Daniel Heck


τ╠┴╫╬┘╩ ╥┴┌╥┴┬╧╘▐╔╦, ╟╥┴╞╔╦┴, ─╧╦╒═┼╬╘┴├╔╤





 Ronald Lamprecht


XML, ╟╥┴╞╔▐┼╙╦╔╩ ╔╬╘┼╥╞┼╩╙, ╨╥╧╟╥┴══╔╥╧╫┴╬╔┼ ╧╙╬╧╫╬╧╩ ▐┴╙╘╔, ─╧╦╒═┼╬╘┴├╔╤





 Andreas Lochmann


≡╥╧╟╥┴══╔╥╧╫┴╬╔┼, ╥╒╦╧╫╧─╙╘╫╧ ╒╥╧╫╬╤═╔, ─╔┌┴╩╬ ╒╥╧╫╬┼╩, ─╧╦╒═┼╬╘┴├╔╤





 Petr Machata


Σ╔┌┴╩╬ ╒╥╧╫╬┼╩, ╨╥╧╟╥┴══╔╥╧╫┴╬╔┼





 Nat Pryce


Σ╔┌┴╩╬ ╒╥╧╫╬┼╩





 Jacob Scott


Σ╔┌┴╩╬ ╒╥╧╫╬┼╩





 Sven Siggelkow


Σ╔┌┴╩╬ ╒╥╧╫╬┼╩ ╔ ╙╨┼├╔┴╠╪╬┘┼ ┌╬┴╬╔╤ Oxyd





 Ralf Westram


≡╥╧╟╥┴══╔╥╧╫┴╬╔┼, ─╔┌┴╩╬ ╒╥╧╫╬┼╩













[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 6.2 ∩╙╧┬┘┼ ┬╠┴╟╧─┴╥╬╧╙╘╔ 





 Johannes Fortmann


≡╧╥╘╔╥╧╫┴╬╔┼ ╬┴ Mac OS X, ╬┼═╬╧╟╧ ╨╥╧╟╥┴══╔╥╧╫┴╬╔╤, ╟╥┴╞╔╦┴





 Dustin Norlander


Σ╔┌┴╩╬┼╥ █╥╔╞╘┴ "Dustismo"





 Jeremy Sawicki


≡┼╥┼╥┴┬╧╘╦┴ ╞╧╥═┴╘┴ ╞┴╩╠┴ Oxyd, Oxydlib





 Erich Schubert


≡┴╦┼╘┘ ─╠╤ Debian/Ubuntu





 Meinolf Schneider


∩╥╔╟╔╬┴╠╪╬┴╤ ╔─┼╤ ╔╟╥┘-≤╨┴╙╔┬╧!





 Andrew "Necros" Sega


φ╒┌┘╦┴ ╫ ═┼╬└ (Pentagonal Dreams)






 David W. Skinner


φ╬╧╟╧ ╒╥╧╫╬┼╩ ─╠╤ ≤╧╦╧┬┴╬┴ ╙ ╙┴╩╘┴
http://users.bentonrea.com/~sasquatch/sokoban















[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 6.3 ≡╧═╧▌╬╔╦╔ 



ε┴█┴ ╨╥╔┌╬┴╘┼╠╪╬╧╙╘╪ ╥┴┌╠╔▐╬┘═ ═┼╬╪█╔═ ╨╧═╧▌╬╔╦┴═:











[ < ]
[ > ]
   
[ << ]
[ Up ]
[ >> ]
   
   
   
   
[Top]
[Contents]
[Index]
[ ? ]



 6.4 Θ╙╨╧╠╪┌╒┼═╧┼ ╨╥╧╟╥┴══╬╧┼ ╧┬┼╙╨┼▐┼╬╔┼ 





 SDL 


http://www.libsdl.org/





 SDL_image


http://www.libsdl.org/SDL_image





 SDL_mixer


http://www.libsdl.org/SDL_mixer





 Lua


http://www.lua.org





 Oxydlib


http://www.sawicki.us/oxyd





 toLua++


http://www.codenix.com/~tolua





 zipios


http://zipios.sourceforge.net





 Xerces C++


http://xml.apache.org/xerces-c













[Top]
[Contents]
[Index]
[ ? ]



Table of Contents













[Top]
[Contents]
[Index]
[ ? ]



About This Document



  This document was generated by GeD on March, 25 2007 using texi2html 1.76.




  The buttons in the navigation panels have the following meaning:




  

     Button 
     Name 
     Go to 
     From 1.2.3 go to
  

  

     [ < ] 
    Back
    previous section in reading order
    1.2.2
  

  

     [ > ] 
    Forward
    next section in reading order
    1.2.4
  

  

     [ << ] 
    FastBack
    beginning of this chapter or previous chapter
    1
  

  

     [ Up ] 
    Up
    up section
    1.2
  

  

     [ >> ] 
    FastForward
    next chapter
    2
  

  

     [Top] 
    Top
    cover (top) of document
       
  

  

     [Contents] 
    Contents
    table of contents
       
  

  

     [Index] 
    Index
    index
       
  

  

     [ ? ] 
    About
    about (help)
       
  






  where the  Example  assumes that the current position is at  Subsubsection One-Two-Three  of a document of the following structure:









 
  This document was generated by GeD on March, 25 2007 using texi2html 1.76.