Logika, rozbor čísel
| V dnešním dílu se vrátíme k základům v Excelu, konkrétně práci s čísly. Přidáme si ale nějaký ten algoritmus doplněný vlastními funkcemi VBA a mozkové závity zaměstná i logika. Programový kód vlastních funkcí je v příloze volně přístupný. Smí být použit ale jen pro studijní, resp. nekomerční využití. |
Jak asi víte, Excel zvládá výpočty s čísly na patnáct platných cifer. To se může zdát jako naprosto dostatečné pro kancelářské užití Office, pro vědecké výpočty už to není optimální. Kupříkladu funkce Fibbonaciho posloupnosti už přestává být použitelná lehce nad číslem 70, v Excelu jen s velkými obtížemi vyzkoušíte algoritmus pro počítání cifer čísla "pí", obecně pak výpočetní technice jako takové dává zabrat faktoriál. Jinými slovy, rychle rostoucí posloupnosti čísel nejsou pro Excel tím pravým. Většinu z nás ovšem tyto skutečnosti nemusí trápit. Vzpomínáte, když byla řeč o vnitřním a vnějším formátu buňky? Vnitřně si Excel počítá se svými patnácti ciframi. Vizuální tvar čísla ovlivní formát buňky. Nezapomeňte, že jeho důsledkem může být chybně zobrazená hodnota. Jako příklad vyzkoušejte součet cifer 1.95 a 1.90 s formátem buňky pro zobrazení jednoho desetinného místa. Stejný formát dejte i buňce se součtem těchto hodnot. Excel ukáže čísla 2.0, 2.0 a 3.9. (Dovolil jsem si zde použít tečku místo desetinné čárky.) Zaokrouhlování s pomocí funkcí listu je zaokrouhlením definitivním a je třeba je zvážit. Každý další výpočet, který se na číslo odvolává, bude obsahovat i chybu vlivem zaokrouhlení. Chyba tak narůstá a výsledek řekněme dvaceti výpočtů může být znehodnocen. Někdy je ale zaokrouhlení dokonce dáno legislativou. Ano, mám teď na mysli účetní zaokrouhlování. Pojďme se podívat na fukce sloužící k zaokrouhlování. 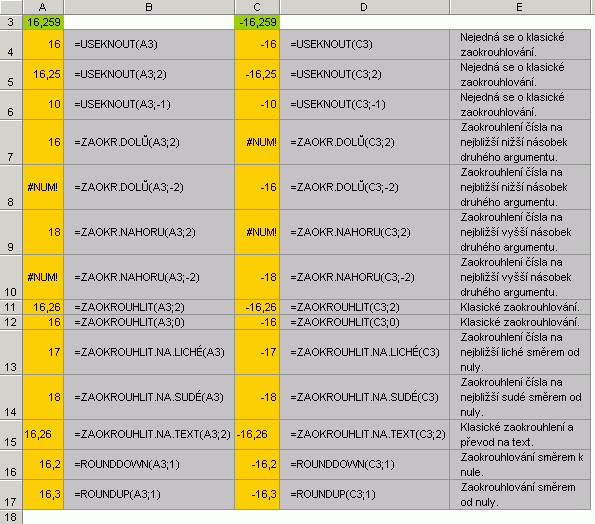 Jak vidíte, funkce nepracují až tak úplně korektně. Poznámka: Budete-li čerpat ze zahraniční literatury, mějte po ruce tabulku funkcí AN-CZ. Funkci ZAOKR.DOLU totiž třeba odpovídá v anglické verzi funkce FLOOR, nikoliv ROUNDDOWN, která český překlad nemá. Vysvětlivku k funkcím představuje další obrázek.  Funkce ROUNDUP a ROUNDDOWN zaokrouhlují číslo na násobky v daném směru. Je-li vaším cílem získat násobek čísla nejbližší dané hodnotě, použijte funkci MROUND (nutno nainstalovat doplněk Analytické nástroje). Zmíněné účetní zaokrouhlování pak může využívat vzorec =ZAOKR.NAHORU(A3;0,5), tj. zaokrouhlování na padesátihaléře směrem nahoru. |
|
Co mi řeknete o daném čísle? Pokud bych obdržel danou otázku, asi bych si vzpomněl na to, že číslo může být liché nebo sudé, kladné nebo záporné, celé, desetinné, přirozené, reálné, komplexní, prvočíslo apod. Směsici funkcí, ať už výpočetních nebo informačních, vlastních i vestavěných, předvádí následující tři obrázky (vše je samozřejmě připraveno k odzkoušení v příloze). 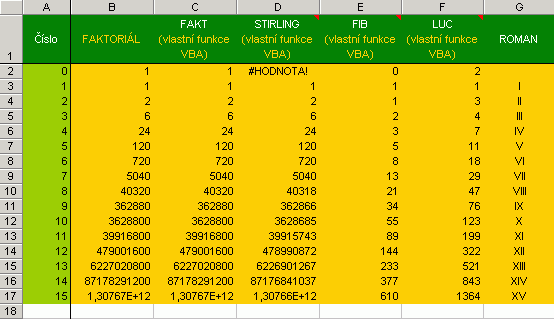
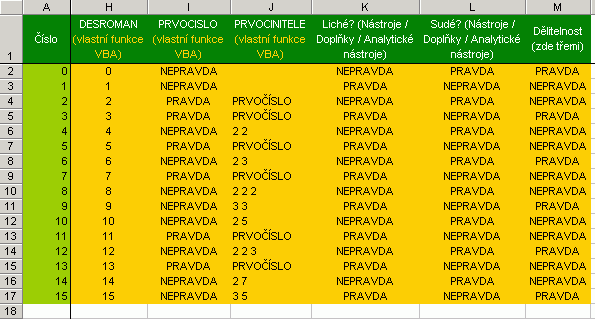
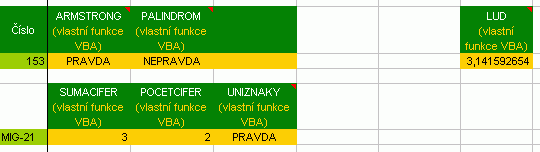
Funkce STIRLING je aproximací faktoriálu (počítačově únosnější algoritmus výpočtu za cenu nepřesnosti), FIB generuje členy Fibbonaciho posloupnosti, LUC členy Lucasovy posloupnosti. DESROMAN je protipólem vestavěné funkce ROMAN (převod římských čísel na desítkové), PRVOCISLO A PRVOCINITELE asi neni treba komentovat. Označení liché-sudé zjišťují funkce ISODD a ISEVEN (viz opět doplněk Analytické nástroje). Dělitelnost řeší funkce MOD (funkce vlastní algoritmům). ARMSTRONG vrací hodnotu PRAVDA, pokud je číslo rovno součtu třetích mocnin svých cifer, PALINDROM vrací PRAVDA, je-li číselná posloupnost symetrická (například 175565571). SUMACIFER a POCETCIFER získává z řetězce číselné hodnoty a dále s nimi počítá, UNIZNAKY pak vrací hodnotu PRAVDA, pokud řetězec obsahuje znaky bez opakování. Některé vlastní funkce (FAKT pro výpočet faktoriálu, LUD pro získání čísla "pí", ...) ačkoliv v Excelu existují, jsou zpracovány v rámci praktikování známých algoritmů. Netvrdím, že jejich zpracování je ideální. A jedeme dál... Pokračujeme zpracováním párů čísel. 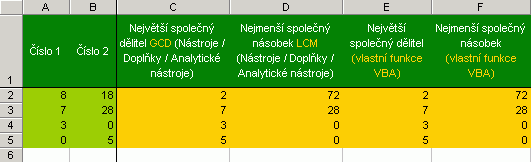


Zde je snad zapotřebí jen vysvětlení dvou funkcí. KONGRUENCE vrací PRAVDA, pokud první i druhé číslo po dělení zvoleným číslem vrací stejný zbytek. PAROVOST testuje, zda-li se jedná o stejnou skupinu znaků řetězce, byť v jiném pořadí. Je to v podstatě test permutace. |
MnožinyMoc se nesmějte, ono to s těmi "hruškami a švestkami" tak jednoduché není :-) Tento odstavec má opět velmi blízko k algoritmizaci úloh a k slibovanému nažhavení mozkových závitů. Jiskřičkou pro zážeh byla skutečnost, že funkce KDYŽ umožňuje pouze sedm křižovatek pro rozhodování. Otázka tedy zněla, zda-li jde snížit počet porovnávání pro základní úlohy. Výsledek posuďte sami. 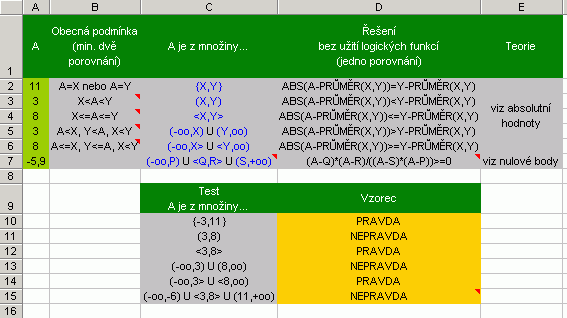 Na základě ukázky lze dospět i k další zajímavé skutečnosti. Obdélníkovou oblast (třeba oblast buněk v listu) lze popsat pouze dvojím porovnáním (viz čtvrtý řádek, operace <= berte jako jedno porovnání). No a když k funkci ABS přidáte ještě SIGN (-1, 0, 1 podle druhu čísla záporné-nula-kladné), dokážete i další věci. 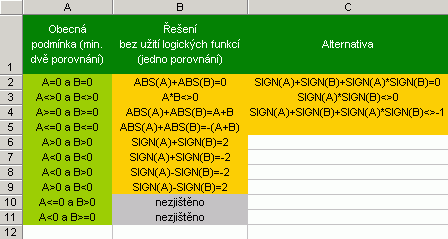 Úlohy pracující s cyklyPředstavte si, že máte v buňkách pod sebou napsané měsíce od ledna do prosince. Když tento seznam vytisknete, vystřihnete a slepíte oba konce k sobě, máte nekonečný cyklus, tak jak funguje i v praxi, tedy po prosince přijde opět leden. Jak ale donutit Excel, aby také považoval rozbalený seznam za cyklus? Jinými slovy, jak donutit třeba vyhledávací funkci aby po prosinci přešla na leden a obráceně? Vyhledávací funkce většinou pracují s indexy, proto si na chvilku zaměňte v duchu měsíce za čísla od 1 do 12 (i = 1, 2, … 12), což znamená naučit Excel, aby po dvanáctce přešel na jedničku. Nazvěme tento případ potřebou resetu cyklu na čísle (R), v našem příkladu resetu na čísle 12. Potřebujeme tedy kontrolovat přetečení proměnné i. Jako první vás asi napadne využít funkce MOD() vracející zbytek čísla po dělení. Pokud ji užijeme ve tvaru MOD(i, R+1), dosáhneme kýženého efektu jen zčásti. Dojde k resetu na R (v našem příkladu R = 12), ovšem následující cyklus začne nulou a nikoliv jedničkou. Přesuňme pozornost k sesterské funkci QUOTIENT vracející celou část po dělení (nutný doplněk Analytické nástroje). Experimentováním jsem u kladných čísel došel ke tvaru = i-R*(QUOTIENT(i-1;R)) Při R = 12 bude vrácená hodnota tedy vždy v rozmezí 1 až 12, a to nikoliv náhodně. Vlastně dochází k jakémusi rozpočítávání do šuplíků 1 až 12. Pro pochopení, číslo 20 na vstupu nám bude vráceno jako 8, což je jeden rok (cyklus) a 8 měsíců (šuplík 8). Připustíme-li výskyt záporných hodnot, pak funkce může mít následující tvar: = SIGN(i)*(ABS(i)-R*(QUOTIENT(ABS(i)-1;R))) Po čase jsem došel k ekvivalentnímu vzorci, který nevyžaduje instalované Analytické nástroje: = i-R*(ROUNDUP(i/R;0)-1) Přehled postupů při práci s cykly (použitelný obecně i ve VBA) znázorňuje obrázek níže. 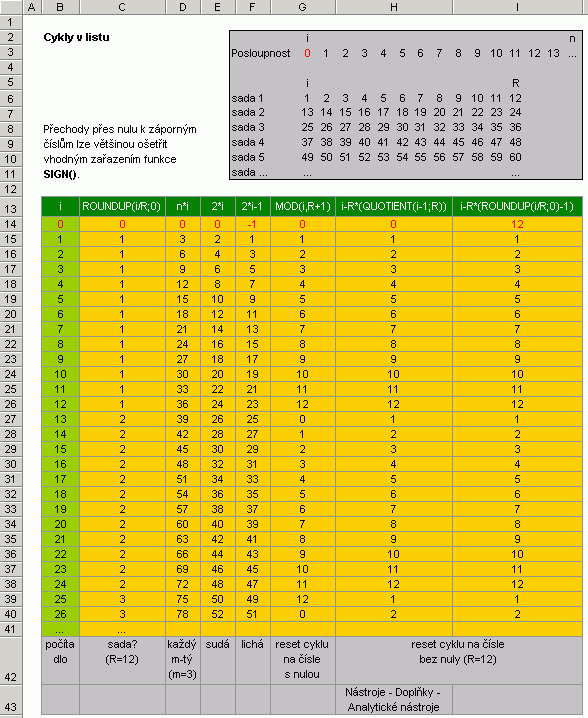 "Čísla v mixéru"Odborník promine, ale tento odstavec jsem tak nazval proto, že jsem nechtěl čtenáře už nadpisem děsit neoblíbenou částí matematiky střední školy. Půjde totiž o kombinace, variace a permutace. Příkladem snad alespoň naznačím, co se skrývá pod jednotlivými pojmy. Cílem bylo navržení funkcí, které generují seskupení čísel v souladu s těmito pojmy. 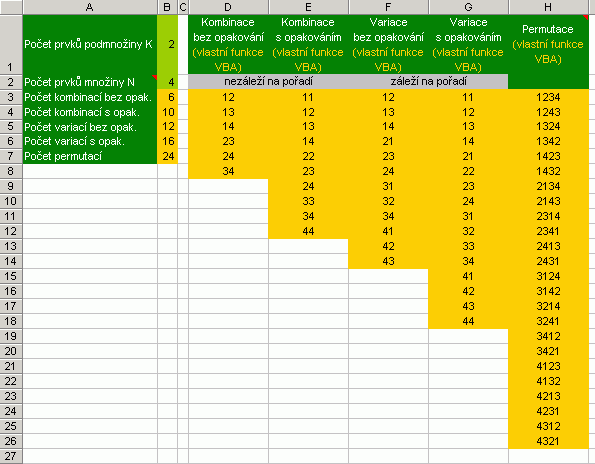 Už slyším čtenáře, kteří říkají, že potřebují funkci, která generuje hesla ze znaků, nikoliv čísel. Tento článek ale nesměřuje přímo k VBA, jen naznačuje možnosti. Napovím pouze tedy, že kupříkladu zápisem 4312 je řečeno: Čtvrtý člen dej na první pozici, třetí na druhou, první přijde na třetí a druhý na poslední. Takže hurá se znaky do pole a ... zbytek je na vás :-) Kód funkcí je totiž volně přístupný... |
|
K vyhodnocování pravdivosti či nepravdivosti výroků slouží tzv. Boolovská algebra. Ta pracuje s dvouhodnotovými proměnnými. Ony dva stavy tvoří známé PRAVDA, NEPRAVDA, v elektrotechnice pak 1 (zapnuto), 0 (vypnuto). Úplnou tabulku elementárních operací dvou proměnných ukazuje následující obrázek (spodní oddělená část je výsledkem experimentování a netvoří základ).  Pracujeme-li s více jak dvěma vstupy, musíme se pohlédnout po teorii. Existují v podstatě dvě. První je známá jako Karnaughovy mapy, se druhou jsem se osobně seznámil mnohem později a je účinnější. Nese název Quine-McCluskey. Cílem obou je minimalizovat funkci (a tedy počet elektronických součástek) potřebnou k řešení problému. Je vám tato technika cizí a zdá se vám nepotřebná? Nemusí tomu tak být. Následující příklad řeší použití odvětrávacího zařízení u tří pecí. Zadání je takové, že odvětrávání se má spustit, jsou-li v provozu alespoň dvě pece. 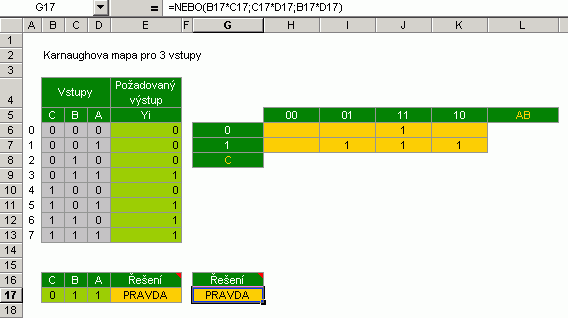 V tuto chvíli nemám zpracovaný obecný algoritmus pro Karnaughovy mapy. Proto je výsledku dosaženo převážně ručně. Na internetu naleznete ovšem řadu samostatných programů na toto téma (Karnaugh Minimizer - http://www.shuriksoft.com, K-V Diagram-Applet a jiné). V momentě, kdy jsem se chystal naprogramovat použitelnější metodu Quine-McCluskey, našel jsem výborný doplněk italského programátora již hotový a navíc zdarma. Jedná se o Binary Arithmetic Package (zkráceně BINUM) a najdete jej na stránkách http://digilander.libero.it/foxes/binum11.zip. |
|
|
Použitá literatura: J. Walkenbach: Excel - vzorce a funkce, Mobil Media, 2001 |