C/C++ & Visual C++
Kurz DirectX (35.)
Úvodem | Datové struktury | Kurz DirectX | Downloads | Otázky a odpovědi
V této lekci se ještě vrátíme k normálovým vektorům terénu. Do teď jsme totiž tyto vektory počítali velice zjednodušeně a dá se říct i nepřesně. Dnes si ukážeme způsob, jak vektory určit přesněji. V další části lekce tyto vektory zobrazíme nad terénem, abychom viděli, že jsou skutečně správně.
35.1. Normálové vektory (2.)
Do dnešní lekce jsme normálový vektor každého vertexu počítali pouze ze dvou směrových vektorů, které byly určeny polohou daného vertexu a jeho sousedy. Tento způsob lze použít v případě, že terén není příliš členitý (tedy nejsou zde náhlé změny výšky vertexu). V tomto případě totiž je vypočtený normálový vektor značně nepřesný. Mezním případem je ostrá hrana. Normála bude kolmá buď k jedné nebo k druhé rovině (podle toho, kde leží uvažované vertexy), což je samozřejmě neodpovídá skutečnosti.
Správně řešení spočívá v tom, že vezmeme v úvahu všechny dílčí normálové vektory rovin přilehlých k daném vertexu a z těchto vektorů pak určíme průměrný normálový vektor.
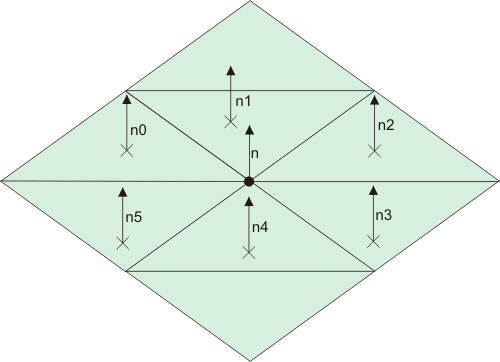
Tedy pro vyznačený vertex se jeho normála spočítá jako průměr vektorů n0 až n5 (dřív jsme vlastně vzali vektor n1 a ten jsme prohlásili za normálu n).
Jak budeme postupovat při výpočtu? Nebude to nic moc složitého. Nejprve vybereme sousedy vertexu, pro který chceme normálu vypočítat. Musíme brát v úvahu to, že ne každý vertex má všech 6 sousedů. Například vrcholy na kraji terénu budou mít o dva sousedy méně, vrcholy na "rohu" dokonce o tři sousedy méně.
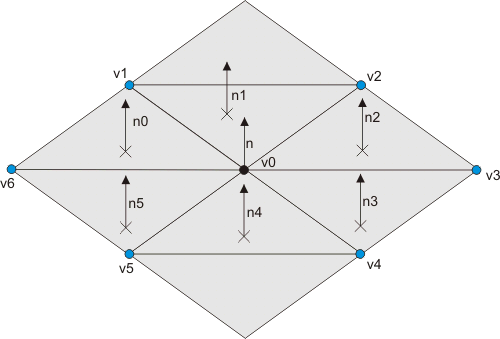
Postupně tedy otestujeme existenci sousedů v1 až v6 a rovnou spočítáme směrový vektor z vektoru v0 výrazem vx - v0 kde vx je v1 až v6. Přitom ještě uložíme informaci, že daný soused skutečně existuje a že ho později musíme brát v úvahu. Kód této části bude vypadat následovně:
// Vektor, pro ktery normalu pocitame - stredovy vektor
v0 = m_arTerrain[x][y].vecPos;
// Nyni vybereme ty spravne body okolo stredoveho vektoru
// a rovnou urcime smerove vektory k temto bodum
if(x < m_iTerrainTilesX)
{
s1 = m_arTerrain[x+1][y].vecPos - v0;
vecMask |= 0x01;
}
if(y < m_iTerrainTilesY)
{
s2 = m_arTerrain[x][y+1].vecPos - v0;
vecMask |= 0x02;
}
if(x > 0 && y < m_iTerrainTilesY)
{
s3 = m_arTerrain[x-1][y+1].vecPos - v0;
vecMask |= 0x04;
}
if(x > 0)
{
s4 = m_arTerrain[x-1][y].vecPos - v0;
vecMask |= 0x08;
}
if(y > 0)
{
s5 = m_arTerrain[x][y-1].vecPos - v0;
vecMask |= 0x10;
}
if(y > 0 && x < m_iTerrainTilesX)
{
s6 = m_arTerrain[x+1][y-1].vecPos - v0;
vecMask |= 0x20;
}
Proměnná vecMask je typu unsigned char nebo BYTE. Ve vektorech s1 až s6 jsou uloženy směrové vektory příslušných vertexů v0 - v6.
V dalším kroku vybere správné sousedy a vypočteme dílčí normály. V proměnné vecMask je nastaven bit pokud existuje směrový vektor, takže dva sousední bity představují dva sousední směrové vektory, ze kterých určíme normálu.
// Spocitame normaly pro sousedni dvojice
// s1 a s2 normala
if(vecMask & 0x03)
{
D3DXVec3Cross(&n, &s1, &s2);
D3DXVec3Normalize(&n, &n);
// Vysledny vektor n0
n0 += n;
// Pocet vektoru pro prumer
iNormCount++;
}
// s2 a s3 normala
if(vecMask & 0x06)
{
D3DXVec3Cross(&n, &s2, &s3);
D3DXVec3Normalize(&n, &n);
// Vysledny vektor n0
n0 += n;
// Pocet vektoru pro prumer
iNormCount++;
}
// s3 a s4 normala
if(vecMask & 0x0C)
{
D3DXVec3Cross(&n, &s3, &s4);
D3DXVec3Normalize(&n, &n);
// Vysledny vektor n0
n0 += n;
// Pocet vektoru pro prumer
iNormCount++;
}
// s4 a s5 normala
if(vecMask & 0x18)
{
D3DXVec3Cross(&n, &s4, &s5);
D3DXVec3Normalize(&n, &n);
// Vysledny vektor n0
n0 += n;
// Pocet vektoru pro prumer
iNormCount++;
}
// s5 a s6 normala
if(vecMask & 0x30)
{
D3DXVec3Cross(&n, &s5, &s6);
D3DXVec3Normalize(&n, &n);
// Vysledny vektor n0
n0 += n;
// Pocet vektoru pro prumer
iNormCount++;
}
// s6 a s1 normala
if(vecMask & 0x41)
{
D3DXVec3Cross(&n, &s6, &s1);
D3DXVec3Normalize(&n, &n);
// Vysledny vektor n0
n0 += n;
// Pocet vektoru pro prumer
iNormCount++;
}
Pro každé dva sousední směrové vektory spočítáme vektorový součin a výsledný vektor normalizujeme na jednotkovou velikost. V proměnné n0 je suma všech dílčích normál. Tento vektor v zápětí podělíme hodnotou iNormCount a získáme konečný normálový vektor jednoho vertexu!
// ulozime vysledny vektor - udelame prumer vsech dilcich normal
m_arTerrain[x][y].vecNormal = n0 / float(iNormCount);
Jako třešničku na dortu vytvoříme konečný vektor jako průměr všech dílčích vektorů přilehlých rovin. Tímto algoritmem spočítáme normály o hodně přesněji než původní verzí. Na druhou stranu výpočet trvá podstatně déle, pro každý vertex totiž voláme funkci D3DXVec3Cross() hned 6x!!!
35.2. Zobrazení normálových vektorů
V druhé části lekce se budeme zabývat tím, jak normály zobrazit u každého vertexu. Normálu zobrazíme jako čáru z příslušného vertexu směrem vzhůru. Výsledek pak bude vypadat jako kdyby na terénu byla dokonale kolmá tráva. Pro každou normálu budeme potřebovat dva body (vertexy). V lokaci máme 128x128 políček takže dohromady to bude 16384 normál s 32768 vrcholy. Vytvoříme tedy pro každou lokaci další vertex buffer. Index buffer nebude v tomto případě potřeba, protože jednotlivé čáry spolu nebudou mít nic společného, tudíž je jakákoliv indexace zbytečná.
struct Location
{
// Jednoznacne ID lokace (pouze kvuli vypisum)
WORD m_wID;
// Index buffer ktery ma indexy v ramci jedny lokace
IIndexBuffer *pIB;
// pocet viditelnych listu
int m_iVisQuads;
int m_iVisTiles;
// Minimalni a maximalni pouzity index
WORD m_iMinIndex;
WORD m_iMaxIndex;
// Docasny pointer na otevreny index buffer
WORD *pIndices;
// Okrajove body
BoundingPoint arBounds[4];
// vertex buffer pro normaly
IVertexBuffer *pNormalsVB;
};
Tento buffer vytvoříme v metodě CreateQuadTree(). Každá lokace má vlastní buffer na normály a velikost jsme odvodili o pár řádků výše:
// Create VB for terrain and copy all locations
if(S_OK == CreateDisplayObject(DISIID_IVertexBuffer, (void**)&m_arLoc[l].pNormalsVB))
{
dwRet = m_arLoc[l].pNormalsVB->Create(2*LOC_V_SIZE*LOC_V_SIZE*sizeof(VERTEX),
D3DUSAGE_WRITEONLY,VERTEXFORMAT,D3DPOOL_DEFAULT);
if(dwRet != S_OK)
{
XException exp("Terrain is not initialized. Cannot create terrain vertex buffer.", dwRet);
THROW(exp);
}
}
Buffer můžeme vytvořit a naplnit ve stejné smyčce jako vertex buffer pro samotné vertexy.
m_pTerrainVB->GetBuffer()->Lock(l*LOC_V_SIZE*LOC_V_SIZE*sizeof(VERTEX),
LOC_V_SIZE*LOC_V_SIZE*sizeof(VERTEX), (BYTE**)&pVertices, 0);
m_arLoc[l].pNormalsVB->GetBuffer()->Lock(0,0, (BYTE**) &NormalsVertices, 0);
for(y = m_arLoc[l].arBounds[0].y; y <= m_arLoc[l].arBounds[3].y; y++)
{
for(x = m_arLoc[l].arBounds[0].x; x <= m_arLoc[l].arBounds[3].x; x++)
{
NormalsVertices[n + 0] = m_arTerrain[x][y];
NormalsVertices[n + 0].dwDiffuse = D3DCOLOR_ARGB(0, 255, 255, 255);
NormalsVertices[n + 1] = m_arTerrain[x][y];
NormalsVertices[n + 1].dwDiffuse = D3DCOLOR_ARGB(0, 255, 255, 0);
NormalsVertices[n + 1].vecPos += m_arTerrain[x][y].vecNormal;
pVertices[i] = m_arTerrain[x][y];
if(m_dwFlags & TF_WRITEBUFFERS)
{
fprintf(f, "%d: %f, %f, %f\n", i+l*LOC_V_SIZE*LOC_V_SIZE, pVertices[i].vecPos.x,
pVertices[i].vecPos.y, pVertices[i].vecPos.z);
}
i++;
n += 2;
}
}
m_arLoc[l].pNormalsVB->GetBuffer()->Unlock();
m_pTerrainVB->GetBuffer()->Unlock();
Modře je vyznačen nový kód ve smyčce. Nejprve uzamkneme příslušný buffer lokace, poté ve dvou vnořených smyčkách nastavíme dva body pro každou normálu. První z těchto bodů je samotný vertex, kterému normála patří. Druhý bod je posunutý ve směru normály (normálový vektor máme již spočítaný). Navíc ještě každému bodu přiřadíme jinou barvu, aby byl vektor pěkně vidět na zeleném terénu. Na závěr buffer samozřejmě odemkneme.
Na úplný závěr lekce ještě ukáži, jak normály vykreslit:
if(m_dwFlags & TF_SHOWNORMALS)
{
pDis->GetDevice()->SetVertexShader(VERTEXFORMAT);
pDis->GetDevice()->SetTexture(0, NULL);
pDis->GetDevice()->SetRenderState(D3DRS_LIGHTING, FALSE);
for(l = m_iLocCount-1; l >= 0; l--)
{
if(m_arLoc[l].m_iVisTiles > 0)
{
pDis->GetDevice()->SetStreamSource(0, m_arLoc[l].pNormalsVB->GetBuffer(), sizeof(VERTEX));
pDis->GetDevice()->DrawPrimitive(D3DPT_LINELIST, 0, LOC_V_SIZE*LOC_V_SIZE);
}
}
pDis->GetDevice()->SetRenderState(D3DRS_LIGHTING, TRUE);
}
Viditelnost normál je závislá na příznaku TF_SHOWNORMALS. Nastavíme standardní parametry jako vertex shader, texturu na NULL, vypneme světlo (normály normál nevedeme) a pak vykreslíme vektory pro každou viditelnou lokaci. Vykreslování normál není příliš efektivní, ale v tomto případě nám samozřejmě nejde o výkon.
35.3. Závěr
Na závěr tu máme obrázek terénu s vykreslenými normálovými vektory:

Příklad si samozřejmě můžete stáhnout v sekci Downloads. Vykreslování normálových vektorů lze zapnout a vypnout klávesou U.
Těším se příště nashledanou.