
Konečně je zde nová lekce programování 3D grafiky. Minule jsme naťukli optimalizační metody, dnes budeme implementovat příklad terénu, který ukáže, že tyto metody jsou skutečně potřeba. Bude se jednat o terén složený z políček, informace o terénu budeme číst buď ze souboru bmp, pak se jedná o techniku heightmap nebo použijeme jeden z mnoha algoritmů na generování náhodné krajiny.
Existuje mnoho algoritmů na tvorbu terénu složených ze čtvercových políček. Tyto políčka jsou složena ze dvou trojúhelníků. Síť takového terénu pak může vypadat takto:

Problém tedy je, jak správně nastavit z-tovou souřadnici jednotlivých vrcholů, aby to ve výsledku vypadalo jako terén. Náhodně přiřazené hodnoty asi nebudou to pravé, pak vznikl velice "ostrá" plocha. Je jasné, že hodnota jednoho vrcholu musí nějak ovlivňovat hodnoty vrcholů kolem. Je mnoho algoritmů, jak tuto úlohu řešit a každý má mnoho modifikací s mírně lišícími se výsledky. V naší lekci použijeme dvě metody tvorby terénu.
1) Tou první bude metoda zvaná heightmap neboli mapa výšek. Jedná se o 2D pole o rozměrech vytvářeného terénu, ve kterém jsou uloženy z-tové souřadnice každého vertexu. Jak ale toto pole naplnit? Nejjednodušší je použít bitmapu, kde barevná informace nese správnou výšku. Pokud použijete monochromatickou bitmapu, je jedno jakou složku barvy berete v úvahu (R = G = B). U barevné je to trochu složitější. V našem případě jsem použil odlišný způsob. Barevná informace bitmapy nese barvu daného vertexu a informaci o výšce nese alpha kanál vytvořený například ve Photoshopu a uložený spolu s bitmapou. Poté bitmapu načteme jako texturu a pomocí metod LockRect() a UnlockRect() načteme potřebnou informaci. Jako příklad uvedu zdrojovou bitmapu terénu a jeho alpha kanál, který je použit pro z-tovou souřadnici vertexů:


2) Za druhé použijeme velice primitivní (ačkoliv dost pomalý) algoritmus "kopců". Je to iterační algoritmus, který vždy vypočítá náhodný střed "kopce" a poté provede v tomto místě vyboulení terénu pomocí funkce kosinus. Tento postup opakuje mnohokrát, takže se na terénu vytváření náhodně vysoké hrbolky. Problém je, že po každém novém kopci se musí projet celé pole vertexů a modifikovat příslušně jejich výšku (u většiny navíc neprovádíme žádnou změnu!), což trvá docela dlouho (když se to má provést 1000x). Výsledek popsaného algoritmu je vidět na dalším obrázku:

Dále jsem implementoval do našeho enginu systém rozhraní. Základem jsou funkce CreateDisplayObject() či CreateInputObject(). Kdo zná technologii COM, vše rychle pochopí. Tento systém totiž pracuje na podobném principu. Každý objekt, který chceme exportovat (většinou se jedná o třídy) neexportujeme přímo, ale exportujeme pouze jeho rozhraní (interface), které obsahuje pouze metody, tedy rozhraní nikdy nemá atributy! Toto rozhraní má jen čistě virtuální metody, je tedy abstraktní a nemůžeme z něj vytvořit objekt. Je třeba zdědit další třídu, která ovšem nebude exportovaná a navíc bude obsahovat implementaci metod rozhraní (dokonce musí, aby šel z této třídy vytvořit objekt) a může mít vlastní atributy. Poté vytvoříme jakýsi manažer objektů, který nám bude vytvářet objekty, tedy již nebude potřeba alokovat paměť pomocí new, to za nás provede manažer. Vše si ukážeme na příkladu. mějme rozhraní IDisplay:
class DISPLAY_API IDisplay
{
public:
virtual HRESULT Init(HWND hWnd) = 0;
virtual HRESULT UpdateBackground() = 0;
virtual HRESULT Present() = 0;
virtual HRESULT RestoreDisplay() = 0;
virtual D3DXVECTOR2* GetResolution() = 0;
virtual ICamera * GetCamera() = 0;
virtual LPDIRECT3DDEVICE8 GetDevice() = 0;
virtual IResourceManager* GetResourceManager() = 0;
virtual D3DFORMAT GetTextureFormat() = 0;
virtual HRESULT EnableLight(int iIndex, BOOL bEnable = TRUE) = 0;
virtual HRESULT SetLight(int iIndex, D3DLIGHT8 * pLight) = 0;
public:
// interface functions
virtual HRESULT AddRef() = 0;
virtual HRESULT Release() = 0;
};
Vidíme pouze čistě virtuální metody bývalé třídy XDisplay. Abychom toto rozhraní mohli použít, je třeba ho exportovat pomocí DISPLAY_API. Třída XDisplay zůstane zachována, ale nyní má základní třídu právě IDisplay a její metody již nejsou čisté a musí být tedy implementovány:
class XDisplay : public IDisplay
{
// D3D objects
IDirect3D8 * m_lpD3DObject;
IDirect3DDevice8* m_lpD3DDevice;
D3DPRESENT_PARAMETERS m_d3dDeviceParam;
DWORD m_dwRef;
//
// Display settings
WORD m_wFlags;
// Display parameters
D3DXVECTOR2 m_sRes;
UINT m_iDepth;
D3DDEVTYPE m_typeDeviceType;
int m_iAdapterOrdinal;
D3DFORMAT m_formatScreenDepth;
D3DFORMAT m_formatTextureDepth;
D3DTEXTUREFILTERTYPE m_tftMagTextureFilter;
D3DTEXTUREFILTERTYPE m_tftMinTextureFilter;
D3DTEXTUREFILTERTYPE m_tftMipTextureFilter;
//
// FPS atributes
float m_fStartTime;
float m_fStopTime;
FLOAT m_Frames;
float m_fCurrentFPS;
float m_fFrameRate;
int m_iDesiredFPS;
char m_szFPSString[50];
char m_szInfoString[512];
//
// Camera
ICamera * m_lpCamera;
I3DFont * m_lpFPSFont;
I3DFont * m_lpInfoFont;
IResourceManager* m_lpResManager;
//
// Time between two frames
float m_fTime;
// Time from app start
float m_fTotalTime;
// Background color
D3DCOLOR m_dwBackgroundColor;
int m_iMaxLights;
private:
int UpdateFPS();
void LimitFPS();
void Clean(void);
void BuildUpMatrices(D3DXVECTOR3 *pvEyePt, D3DXVECTOR3 *pvLookAtPt);
public:
virtual HRESULT Init(HWND hWnd);
virtual HRESULT UpdateBackground();
virtual HRESULT Present();
virtual HRESULT RestoreDisplay();
virtual D3DXVECTOR2* GetResolution() { return &m_sRes;}
virtual ICamera * GetCamera() {return m_lpCamera;}
virtual IResourceManager* GetResourceManager() {return m_lpResManager; }
virtual LPDIRECT3DDEVICE8 GetDevice() {return m_lpD3DDevice;}
virtual D3DFORMAT GetTextureFormat() {return m_formatTextureDepth;}
virtual HRESULT EnableLight(int iIndex, BOOL bEnable = TRUE);
virtual HRESULT SetLight(int iIndex, D3DLIGHT8 * pLight);
public:
virtual HRESULT AddRef();
virtual HRESULT Release();
XDisplay(void);
~XDisplay(void);
};
Navíc třída obsahuje soukromé atributy a všimněte si, že není exportována z knihovny! K čemu jsou metody AddRef() a Release()? Uvnitř třídy naleznete atribut m_dwRef, ve kterém je uložen počet referencí na tento objekt, tedy počet uživatelů používající tento objekt. Kdykoliv zavoláte funkci CreateDisplayObject() je toto počítadlo inkrementováno metodou AddRef() a když uživatel již nepotřebuje objekt, uvolní jeho rozhraní metodou Release(), která sníží reference. Zároveň pokud počet referencí klesne na 0, čili objekt již není používán, objekt se sám zruší. Je tedy duležité při získání rozhraní ho také uvolnit, jinak objekt zůstane viset v paměti. Rozhraní jsou uložena v souboru Interfaces.h. Jak ale vypadá ona záhadná funkce CreateDisplayObject()? Ve skutečnosti je velice primitivní:
// Call This function to get desired interface
DISPLAY_API HRESULT CreateDisplayObject(DISIID InterfaceID, void ** ppv)
{
// unique objects
static IDisplay * g_theDisplay = NULL;
static ICamera * g_theCamera = NULL;
static IResourceManager * g_theResourceManager = NULL;
if(!ppv)
{
return ERROR_INVALID_PARAMETER;
}
// get pointer according IID
switch(InterfaceID) {
case DISIID_IDisplay:
if(!g_theDisplay)
{
*ppv = g_theDisplay = new XDisplay;
}
else {
*ppv = g_theDisplay;
}
((IDisplay*)(*ppv))->AddRef();
break;
case DISIID_ICamera:
if(!g_theCamera)
{
*ppv = g_theCamera = new XCamera;
}
else {
*ppv = g_theCamera;
}
((ICamera*)(*ppv))->AddRef();
break;
case DISIID_IResourceManager:
if(!g_theResourceManager)
{
*ppv = g_theResourceManager = new XResourceManager;
}
else {
*ppv = g_theResourceManager;
}
((IResourceManager*)(*ppv))->AddRef();
break;
case DISIID_IVertexBuffer:
*ppv = new XVertexBuffer;
((IVertexBuffer*)(*ppv))->AddRef();
break;
case DISIID_IIndexBuffer:
*ppv = new XIndexBuffer;
((IIndexBuffer*)(*ppv))->AddRef();
break;
case DISIID_IMesh:
*ppv = new XMesh;
((IMesh*)(*ppv))->AddRef();
break;
case DISIID_ITexture:
*ppv = new XTexture;
((ITexture*)(*ppv))->AddRef();
break;
case DISIID_I3DObject:
*ppv = new X3DObject;
((I3DObject*)(*ppv))->AddRef();
break;
case DISIID_I3DFont:
*ppv = new XFont;
((I3DFont*)(*ppv))->AddRef();
break;
default:
return E_NOINTERFACE;
}
return S_OK;
}
Má dva parametry, prvním určíme, jakého objektu chceme rozhraní a do druhé se uloží přímo ukazatel na požadované rozhraní. Pokud uživatel požádá o rozhraní, které není podporováno, funkce vrací E_NOINTERFACE. První tři objekty jsou zvláštní tím, že jsou unikátní, čili funkce je vytvoří při prvním volání, poté vrací jen ukazatel a inkrementuje reference. Ukazatele jsou uchovány v podobě statických proměnných přímo ve funkci. Další objekty jsou vždy nově vytvořeny. Identifikátory rozhraní jsou definovány v souboru manager.h jako typ enum:
// Interface ids
enum DISIID
{
DISIID_IDisplay,
DISIID_ICamera,
DISIID_IIndexBuffer,
DISIID_IVertexBuffer,
DISIID_IMesh,
DISIID_IResourceManager,
DISIID_ITexture,
DISIID_I3DObject,
DISIID_I3DFont
};
Své rozhraní má každá třída, kterou chceme použít i vně dynamické knihovny. Tento systém je zaveden i v knihovně Input. Nyní můžete odkudkoliv zavolat funkci CreateDisplayObject(DISIID_IDisplay, (void**) pDis) a získat tak rozhraní unikátního objektu XDisplay. Máte zaručeno, že funkce vrátí rozhraní na tentýž objekt (který byl vytvořen při prvním volání s těmito parametry), ale je třeba ho správně uvolnit metodou Release() po ukončení práce s tímto rozhraním. Po této úpravě se nám velice zjednoduší život.
Abychom mohli použít osvětlení Direct3D, je třeba každému vrcholu terénu přiřadit správný normálový vektor, tedy vektor kolmý na plochu. Princip je docela jednoduchý a kdo má za sebou vektorovou algebru, jistě pro něj nebude problém uvedený algoritmus implementovat. Potřebujeme určit rovinu, ve které leží daný vrchol a normála této roviny je i normála vrcholu. Tuto rovinu určíme ze sousedních vrcholů. Budeme-li nároční, budeme počítat normálu ze všech 4 sousedních vrcholů. V našem případě se ale spokojíme s jednodušším řešením a postačí nám pouze dva sousední vrcholy. Na následujícím obrázku je to všechno rozkreslené:
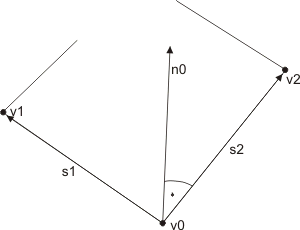
Na obrázku je v0 vrchol, pro který chceme spočítat normálu, v1 a v2 jsou dva sousedi, pomocí kterých určíme rovinu, s1 a s2 jsou dva směrové vrcholy ležící v rovině, k níž je normálový vektor n0 kolmý. Vektory s1 a s2 spočítáme velice jednoduše, protože známe počáteční i koncové body, pak s1 = v0 - v1 a s2 = v0 - v2. Dále použijeme vektorový součin, který přesně vypočte vektor n0 (vektorový součin dvou vektorů vrátí vektor kolmý k oběma vektorům). Je třeba si dát pozor, aby vektory s1 a s2 měly správnou orientaci, protože v opačném případě by vektor n0 měl opačnou orientaci, tudíž pod terén. Výsledkem by byla tma. Menší problém nastává na hranách terénu neboť krajní vrcholy nemají ty správné sousedy, takže vektor spočítáme ze sousedů, které jsou blíže k počátku.
for(int y = 0; y < g_pHeightMap->Height(); y++)
{
for(int x = 0; x < g_pHeightMap->Width(); x++)
{
v0 = arTerrain[x][y].vecPos;
if(x < g_pHeightMap->Width()-1)
{
z1 = arTerrain[x+1][y].vecPos.z;
}
else
{
z1 = arTerrain[x-1][y].vecPos.z;
}
if(y < g_pHeightMap->Height()-1)
{
z2 = arTerrain[x][y+1].vecPos.z;
}
else
{
z2 = arTerrain[x][y-1].vecPos.z;
}
v1 = D3DXVECTOR3(float(x+1), float(y), z1);
v2 = D3DXVECTOR3(float(x), float(y+1), z2);
s1 = v0 - v1;
s2 = v0 - v2;
// create normal vector
D3DXVec3Cross(&n0, &s1, &s2);
D3DXVec3Normalize(&n0, &n0);
arTerrain[x][y].vecNormal = n0;
}
}
Knihovna D3DX naštěstí obsahuje plno podpůrných funkcí pro práci s vektory, takže výpočet bude docela jednoduchý. Vypočet provedeme pro každý vrchol v terénu, do v0 uložíme pozici daného vrcholu a poté nalezneme výšku dvou sousedů. U krajních vertexů je třeba použít jiné dva sousedy. Dále spočteme pozici sousedů (již víme výšku) a určíme směrové vektory s1 a s2 (zde využíváme přetížený operátor - pro objekt D3DXVECTOR3). Nakonec pomocí funkce D3DXVec3Cross() spočteme vektorový součin vektorů s1 a s2 a tento vektor normalizujeme. Vektor bude mít po normalizaci velikost 1. Na závěr vektor přiřadíme danému vrcholu.
Pokud by vám takovýto výpočet nestačil, použijte druhý zmíněný způsob (asi správnější), kdy vypočtete normálu z každých dvou sousedních sousedů daného vektoru, tak získáte 4 normály, ze kterých uděláte průměrný výsledný vektor n0. Tento způsob je popsán na dalším obrázku:
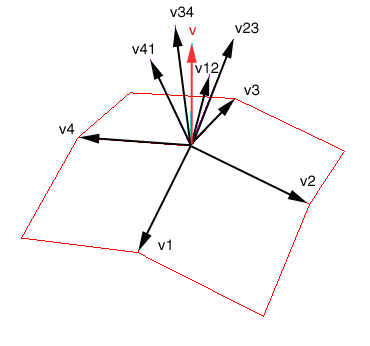
Dále se zaměříme na přečtení potřebných informací ze zdrojové bitmapy. Z obrázku vytvoříme klasickou texturu:
// set parameters according terrain method
dwRet = CreateDisplayObject(DISIID_ITexture, (void**)&g_pHeightMap);
if(dwRet == S_OK)
{
dwRet = g_pHeightMap->LoadTextureFromFile("default.bmp");
if(dwRet != S_OK)
{
XException exp("Cannot load texture for heightmap!", dwRet);
THROW(exp);
}
//set dim of the terrain according dim of the height map
g_iTerrainTilesX = g_pHeightMap->Width() - 1;
g_iTerrainTilesY = g_pHeightMap->Height() - 1;
g_iTerrainVerticesX = g_pHeightMap->Width();
g_iTerrainVerticesY = g_pHeightMap->Height();
}
A rovněž si uložíme rozměry terénu dané velikostí textury, tím pádem jsme omezení na textury o rozměrech 128x128, 128x64 atd. V proměnné g_iTerrainTilesX je počet políček ve směru osy X, v g_iTerrainVerticesX je počet vrcholů ve směru osy X. Vytvoření vertex a index bufferu si necháme na později, ale určitě vytvoříme funkci FillTerrainBuffers(), která načte data z heightmapy a aplikuje výše popsané algoritmy. Poté jen spočítá normály, přesype data do vertex bufferu a vypočte obsah index bufferu. Pro nás teď bude důležitá první část:
VERTEX **arTerrain;
arTerrain = new VERTEX*[g_iTerrainVerticesX];
for(i = 0; i < g_iTerrainVerticesX; i++)
{
arTerrain[i] = new VERTEX[g_iTerrainVerticesY];
}
D3DLOCKED_RECT lr;
g_pHeightMap->GetTexture()->LockRect(0, &lr, NULL, D3DLOCK_READONLY);
TEXTURE_PIXEL * data = (TEXTURE_PIXEL*)lr.pBits;
i = 0;
for(int y = 0; y < g_iTerrainVerticesY; y++)
{
for(int x = 0; x < g_iTerrainVerticesX; x++)
{
arTerrain[x][y].vecPos = D3DXVECTOR3(float(x), float(y), float(data[i].a)/255.0f*10.0f);
arTerrain[x][y].dwDiffuse = D3DCOLOR_ARGB(255,data[i].r,data[i].g,data[i].b);
arTerrain[x][y].tu1 = (x % 2) ? 1.0f : 0.0f;
arTerrain[x][y].tv1 = (y % 2) ? 1.0f : 0.0f;
arTerrain[x][y].vecNormal = D3DXVECTOR3(0.0f, 0.0f, 1.0f);
i++;
}
}
g_pHeightMap->GetTexture()->UnlockRect(0);
Zde nejprve vytvoříme dynamické 2D pole vertexů. Pak voláme metodu LockRect() textury. Tato metoda uzamkne textutu heightmapy a vrátí strukturu D3DLOCKED_RECT, ve které je ukazatel na data textury. Je to pole o stejných rozměrech jako textura. V tomto poli jsou uloženy barevné informace textury a samozřejmě také alpha kanál. Data jsou rozdělena po 4 bytech, kde první byte je modrá složka, druhá je zelená, třetí je červená a čtvrtá je hodnota alpha kanálu, který použijeme pro výpočet výšky vertexu v daném místě textury (každému vertexu přísluší jeden pixel textury). Pro tento účel použijeme strukturu TEXTURE_PIXEL:
struct TEXTURE_PIXEL
{
BYTE b;
BYTE g;
BYTE r;
BYTE a;
};
Která obsahuje barevné složky a alpha kanál pixelu na daném místě textury. Hodnota alpha se může měnit v rozmezí 0-255, proto toto číslo podělíme 255.0, abychom dostali hodnotu v rozmezí 0-1.0 a dále pracujeme s tím rozsahem (v našem případě ho pouze vynásobíme 10.0). Normálové vektory zinicializujeme do neškodného stavu, to je směr vzhurů. Také musíme správně nastavit texturové souřadnice. Pro liché vertexy nastavujeme hodnotu 0.0f, pro sudé 1.0f a to ve směru X i Y. Na závěr je třeba texturu odemknout metodou UnlockRect().
Nyní přejdeme k vlastní podstatě terénu. Již jsem uvedl, že terén je složen z políček, kde každé políčko obsahuje 4 vrcholy a tedy dva trojúhelníky:
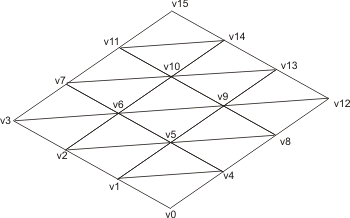
Například první políčko je složeno z trojúhelníků v0, v1, v4 a v1, v5, v4. A v tomto pořadí také budou uloženy indexy těchto vrcholů: 0,1,4,1,5,4. Výpočet indexů tedy už budeme provádět pro každé políčko (nikoliv pro každý vrchol):
WORD *pIndices;
dwRet = g_pTerrainIB->GetBuffer()->Lock(0, 0, (BYTE**)&pIndices, 0);
i = 0;
for(int y = 0; y < g_iTerrainTilesY; y++)
{
for(int x = 0; x < g_iTerrainTilesX; x++)
{
pIndices[i + 0] = x + y * g_iTerrainVerticesX;
pIndices[i + 1] = (x+1) + y * g_iTerrainVerticesX;
pIndices[i + 2] = x + (y+1) * g_iTerrainVerticesX;
i += 3;
pIndices[i + 0] = (x+1) + y * g_iTerrainVerticesX;
pIndices[i + 1] = (x+1) + (y+1) * g_iTerrainVerticesX;
pIndices[i + 2] = x + (y+1) * g_iTerrainVerticesX;
i += 3;
}
}
dwRet = g_pTerrainIB->GetBuffer()->Unlock();
Nejdříve samozřejmě musíme zamknout index buffer. V každém cyklu inicializujeme indexy pro jedno políčko, je vidět, že pro jedno políčko budeme potřebovat 6 indexů (z toho zároveň plyne požadavek na velikost index bufferu). První tři řádky jsou indexy pro první trojúhelník, poté se přesuneme na druhý (jedná se o vypočet indexů ve 2D poli vrcholů). Na závěr nezapomeňte buffer odemknout.
Nyní tedy víme, jak velké mají být vertex a index buffery. Ty můžeme vytvořit hned po načtení heightmapy:
dwRet = CreateDisplayObject(DISIID_IVertexBuffer, (void**) &g_pTerrainVB);
if(dwRet == S_OK)
{
g_dwTerrainVBSize = g_iTerrainVerticesX * g_iTerrainVerticesY * sizeof(VERTEX);
g_dwVerticesCount = g_iTerrainVerticesX * g_iTerrainVerticesY;
dwRet = g_pTerrainVB->Create(g_dwTerrainVBSize, D3DUSAGE_WRITEONLY, VERTEXFORMAT, D3DPOOL_DEFAULT);
if(dwRet != S_OK)
{
XException exp("Cannot create VB for terrain!", dwRet);
THROW(exp);
}
}
dwRet = CreateDisplayObject(DISIID_IIndexBuffer, (void**) &g_pTerrainIB);
if(dwRet == S_OK)
{
g_dwTerrainIBSize = g_iTerrainTilesX * g_iTerrainTilesY * 6 * sizeof(WORD);
g_dwIndicesCount = g_iTerrainTilesX * g_iTerrainTilesY * 6;
dwRet = g_pTerrainIB->Create(g_dwTerrainIBSize, D3DUSAGE_WRITEONLY, D3DFMT_INDEX16, D3DPOOL_DEFAULT);
if(dwRet != S_OK)
{
XException exp("Cannot create IB for terrain!", dwRet);
THROW(exp);
}
}
Velikost vertex bufferu je přímo daná počtem pixelů textury. Metoda Create() rozhraní IVertexBuffer ovšem požaduje velikost v bytech, takže hodnotu musíme vynásobit velikostí struktury VERTEX. U index bufferu jsme si řekli, že pro každé políčko budeme potřebovat 6 indexů. Počet políček je g_iTerrainTilesX * g_iTerrainTilesY. Opět je zde požadována velikost v bytech a tudíž je třeba násobit hodnotu velikostí WORDu (indexy jsou 16-ti bitové).
Po přesypaní dat z 2D pole, vytvořeného na začátku funkce FillTerrainBuffers(), již není toto pole potřeba a proto ho zcela vymažeme z paměti.
V této podkapitole stručně popíšu jak pracuje algoritmus kopečků. Jak jsem uvedl na začátku lekce, algoritmus vytváří na povrchu jakési kopečky o daném poloměru circle size. Tyto kopečky mají několik parametrů, které lze libovolně měnit, třeba i náhodně:
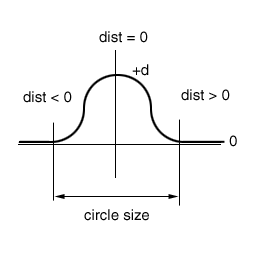
Vertexy uvnitř tohoto poloměru jsou vyboulené podle funkce kosinus, vertexy vně zůstanou nezměněny. Na následujícím obrázku vidíme jeden kopeček:

Na začátku nastavíme výšku všech vertexů na určitou základní hodnotu. Dále opakovaně vytváříme kopečky na náhodných místech mapy a s náhodnými parametry. Složitost terénu závisí na počtu iterací hlavního cyklu, teda na počtu kopečků. Výpis algoritmu:
void CircleAlgorithm(VERTEX **arVertices, int dimX, int dimY)
{
int iCircleX, iCircleY;
char per[50];
double pd, circlesize, distance, disp, fPer = 0.0f;
int iIterCount = cmnReadSetupInt(_S_TERRAIN, _S_ITERCOUNT);
int iDisplacement = cmnReadSetupInt(_S_TERRAIN, _S_DISPLACEMENT);
int iMaxHeight = cmnReadSetupInt(_S_TERRAIN, _S_MAXHEIGHT) * 10.0f;
// reset terrain
for(int y = 0; y < dimY; y++)
{
for(int x = 0; x < dimX; x++)
{
arVertices[x][y].vecPos.z = -10.0f;
}
}
for(int i = 0; i < iIterCount; i++)
{
// choose random circle center
iCircleX = rand() % dimX;
iCircleY = rand() % dimY;
circlesize = (rand() % iMaxHeight) / 10.0f + 10.0f;
disp = (rand() % iDisplacement) / 10.0f;
// apply displacement
for(int y = 0; y < dimY; y++)
{
for(int x = 0; x < dimX; x++)
{
// compute distance current point and center point
distance = sqrt(pow(arVertices[iCircleX][iCircleY].vecPos.x - arVertices[x][y].vecPos.x, 2) + pow(arVertices[iCircleX][iCircleY].vecPos.y - arVertices[x][y].vecPos.y, 2));
pd = distance * 2 / circlesize;
if(fabs(pd) <= 1.0f)
{
arVertices[x][y].vecPos.z += float(disp / 2 + cos(pd * D3DX_PI) * disp / 2);
}
}
}
fPer += (100.0f/iIterCount);
g_pDisplay->UpdateBackground();
g_pDisplay->GetDevice()->BeginScene();
sprintf(per, "Generating terrain: %3.1lf%%", fPer);
g_pKeys->Draw(per, 0, 50, D3DCOLOR_ARGB(255,255,255,0));
g_pDisplay->GetDevice()->EndScene();
g_pDisplay->Present();
}
}
Parametrem disp určíme míru "vyboulenosti" kopečku. Tuto hodnotu volíme náhodně, ale krajní hodnotu načítáme z konfiguračního souboru. Vyboulení je závislé na vzdálenosti středového vertexu a vertexu, pro který počítáme výšku. Tuto vzdálenost spočítáme jako vzdálenost dvou bodů v rovině (druhá odmocnina součtu druhých mocnin rozdílů x-ových a y-ových souřadnic obou bodů). Proměnná pd je menší než 1.0 pokud je vertex v okolí středu kopce a v tomto případě aplikujeme vyboulení. V opačném případě s vertexem nebudeme hýbat, protože je mimo dosah vytvářeného kopce. Posledních 7 řádku jen vypíše informaci o průběhu vytváření terénu, protože to je časově docela náročné. Protože ještě neběží obnovovací smyčka, je třeba prohazovat buffery uměle.
Algoritmus umožňuje mnoho modifikací a to nejen změnou parametrů, ale můžete například jinou funkci než kosinus a vytvářet tak jiné tvary kopců.
Na závěr lekce si povíme, jak terén vykreslit. Zde nastává malý problém kvůli omezení počtu vykreslovaných trojúhelníků. Většina grafických karet umožňuje vykreslovat pouze 65536 primitiv během jednoho volání metody DrawIndexedPrimitive(). Pokud máme terén o rozměrech 128x128 je všechno v pořádku, protože pak budeme mít pouze 32258 trojúhelníků. Pokud ale zkusíte terén 256x256 narazíte, protože 130050 trojúhelníku najednou prostě nevykreslíte. Takže největší terén, který můžeme vytvořit na jedno volání DrawIndexedPrimitive() je 128x256 s 64770 trojúhelníky. Řešení tohoto problému je celkem prosté, volat vykreslovací funkci víckrát s jinými parametry. My se s tím však nebudeme zabývat, protože terén beztak nebudeme vykreslovat najednou (dnes tedy ano, ale dnes také nepoužíváme žádnou optimalizační metodu a spoléháme pouze na hrubý výkon grafické karty a procesoru). Dáme tedy do programu test na správnou velikost textury.
g_pDisplay->GetDevice()->BeginScene();
g_pDisplay->GetDevice()->SetVertexShader(VERTEXFORMAT);
g_pDisplay->GetDevice()->SetStreamSource(0, g_pTerrainVB->GetBuffer(), sizeof(VERTEX));
g_pDisplay->GetDevice()->SetIndices(g_pTerrainIB->GetBuffer(), 0);
g_pDisplay->GetDevice()->SetTexture(0, g_pTerrainSurface->GetTexture());
g_pDisplay->GetDevice()->DrawIndexedPrimitive(D3DPT_TRIANGLELIST, 0, g_dwVerticesCount, 0, g_dwIndicesCount / 3);
g_pDisplay->GetDevice()->EndScene();
Na samotném vykreslení není nic, co bychom neprobírali v minulých lekcích. Voláme metodu pro připravení scény BeginScene(), dále nastavujeme formát vertexů, zdrojový vertex buffer, index buffer a texturu travičky, pak vykreslíme celý terén voláním DrawIndexedPrimitive(), na závěr ukončíme scénu metodou EndScene(). Proměnná g_dwIndicesCount obsahuje počet indexů, již víme, že na každý trojúhelník připadají tři indexy, stačí tedy tuto hodnotu podělit třemi a získáme počet trojúhelníků.
Všimněte, že pokud vytvoříte větší terén, vaše grafická karta přestane stíhat vykreslovat terén s rozumným FPS. Ono také vykreslovat vše není to pravé a v příští lekci si tedy ukážeme jak tento NEDOSTATEK vylepšit.
Těším se příště nashledanou.