DneÜnφ lekce bude ryze teoretickß. ZaΦneme si povφdat o optimalizaΦnφ metod∞ quadtree, kterou v nßsledujφcφ lekci pou₧ijeme na vykreslovßnφ komplexnφho terΘnu. Lekce tedy nebude tentokrßt obsahovat p°φklad, to si ale vynahradφme p°φÜt∞, kdy vytvo°φme novou aplikaci, vyu₧φvajφcφ nßÜ "engine" a hlavn∞ dnes popsanΘ principy.
Optimalizace v oblasti grafiky mß nesmφrn² v²znam, proto₧e i dneÜnφ v²konnΘ karty majφ svß omezenφ a pl²tvat jejich potencißlem (jak je dneska v m≤d∞ a nemusφ se jednat pouze o grafickΘ karty) je krajn∞ nevhodnΘ! Engine, kter² se nezab²vß optimalizacemi vykreslovßnφ dat a spolΘhß jen na hrubou sφlu grafickΘho Φipu, nikdy nem∙₧e b²t ·sp∞Ün². Tohle pochopil John Carmack a vytvo°il nap°φklad genißlnφ engine Quake3, na kterΘm b∞₧φ mnoho her i dnes, 4 roky po uvedenφ hry Quake 3.
My se pochopiteln∞ nebudeme zab²vat takto slo₧it²mi algoritmy, ale n∞kde zaΦφt musφme. Jedna z Φast²ch ·loh v Direct3D je vykreslovßnφ komplexnφ plochy a nemusφ se jednat pouze o terΘn. Metod optimalizace vykreslovßnφ terΘnu je spousta, nap°φklad Quadtree, kter² si rozebereme v dneÜnφ lekci, OctTree se hodφ pro slo₧it∞jÜφ terΘny nebo t°eba LOD (Level of Detail), kde pro zm∞nu nahrazujeme vφc podobn∞ polo₧en²ch polygon∙ jednφm a tφm snφ₧φme celkov² poΦet polygon∙.
V∙bec nejlepÜφ optimalizace je nevykreslovat nic. Pak mßme zaruΦeno, ₧e nßÜ engine bude nejrychlejÜφ na sv∞t∞. ProblΘm bude pravd∞podobn∞ s vyu₧itφm. Prvnφm ·kolem je tedy vykreslovat pouze ta data, kterß jsou skuteΦn∞ vid∞t. Vzpome≥te si na minulou lekci, kdy₧ jsme probφrali kameru. M∞li jsme tam jak²si Φty°st∞n (frustrum), uvnit° kterΘho byla vÜechna data vid∞t, data umφst∞nß vn∞ tohoto objektu se nevykreslujφ. Direct3D se samo starß o to, aby se zbyteΦn∞ nevykreslovala data, kterß jsou ji₧ mimo, jen tato vlastnφ optimalizace nenφ nic extra a ani b²t nem∙₧e, proto₧e Direct3D ji₧ nevidφ logickΘ uspo°ßdanφ dat, o to se tedy musφme postarat my. ╚φm lΘpe a rychleji rozliÜφme, kterΘ polygony vykreslit a kterΘ ne, tφm bude nßÜ engine lepÜφ. Bohu₧el toto nenφ zrovna lehkß ·loha a pan Carmack by z°ejm∞ v₧dy naÜel dalÜφ °eÜenφ, kterΘ by bylo jeÜt∞ rychlejÜφ ne₧ to naÜe! Chce to rovn∞₧ po°ßdnou dßvku zkuÜenostφ s programovßnφm a tφm nemßm te∩ na mysli pouze grafiku.
Druh²m pohledem na optimalizaci m∙₧e b²t snaha o snφ₧enφ poΦtu polygon∙, kterΘ se urΦit∞ musφ vykreslit. V p°φpad∞ terΘnu je to prßv∞ technika LOD, kdy nahrazujeme vφce podobn∞ umφst∞n²ch polygon∙ jednφm (sni₧ujeme vlastn∞ detail terΘnu). Pokud vykreslujeme slo₧it∞jÜφ objekty naΦφtanΘ ze soubor∙ .x, je dobrΘ vytvß°et rozumn∞ slo₧itΘ modely. Docela dobrΘ pravidlo je vytvß°et modely s co nejmenÜφm poΦtem polygon∙ tak, aby v²sledn² model m∞l reßlnΘ tvary. M∙₧ete pou₧φt i vφce model∙ a potΘ vybφrat jednoduÜÜφ model na pomalejÜφch kartßch a naopak. DalÜφ mo₧nost je pou₧φvat billboardy mφsto prav²ch 3D objekt∙. O billboardech jsme se povφdali ji₧ v minulΘ lekci a nynφ ji₧ nenφ problΘm takov² objekt vytvo°it a sprßvn∞ nasm∞rovat pomocφ billboard matice ulo₧enΘ v naÜφ kame°e.
Poslednφ optimalizaΦnφ krok, kde m∙₧eme takΘ nahnat n∞jakΘ ty FPS navφc, se t²kß textur. Zde platφ podobnΘ pravidlo jako u objekt∙. Je pot°eba vytvß°et sprßvn∞ velkΘ textury, aby byl v²sledek vizußln∞ p∞kn² - rozblitΘ textury nejsou na objektech zrovna moc hezkΘ a kdy₧ je textura zbyteΦn∞ velkß, dochßzφ k jejφmu smrÜt∞nφ a to taky nenφ dobr² efekt, navφc pak dochßzφ k zbyteΦnΘmu pl²tvßnφ v²konu. Pou₧φvejte mipmapping, kde to jen jde! Ten vßm ΦßsteΦn∞ zaruΦφ, ₧e textura bude v po°ßdku a¥ budete blφzko Φi daleko od objektu. Toto je vykoupeno vyÜÜφ pam∞¥ovou nßroΦnostφ, proto₧e mipmapovΘ textury zabφrajφ mnohem vφce mφsta v pam∞ti.
Nynφ si p°edstavte, ₧e mßte plochu slo₧enou ze ΦtvereΦk∙ podobn∞ jako ve h°e Transport Tycoon (Deluxe). V Direct3D mß ka₧dΘ polφΦko minimßln∞ 2 troj·helnφky (m∙₧ete d∞lat polφΦka i ze 4 troj·helnφk∙). V Tycoon je plocha slo₧ena asi z 120x120 polφΦky, poΦφtejme tedy 120x120 = 14400 polφΦek na celΘ ploÜe. Mßme tedy 28800 troj·helnφk∙ a to je pouze na terΘn, dalÜφch 50 000 polygon∙ mohou zabφrat stromy. Ve skuteΦnosti je ale povrch 120x120 hrozn∞ malinkat². Ud∞lejme tedy 256x256 (proΦ takovΘ rozm∞ry, uvidφme za chvilku). To u₧ mßme 65536 polφΦek a troj·helnφk∙ tedy bude 2x tolik - 131072. To u₧ je docela sφla, nemyslφte? Kdybychom m∞li vykreslovat v ka₧dΘm cyklu takovΘ mno₧stvφ polygon∙, tak bychom FPS ukazatel moc vysoko nedostali - navφc by to z programßtorskΘho hlediska byla "prasßrna na n-tou". A to se jednß pouze o povrch, kter² vlastn∞ obsahuje minimum polygon∙ z celΘ scΘny (z dalÜφch 500 000 polygon∙ m∙₧ou b²t dalÜφ objekty atd.).
NßÜ problΘm je tedy jasn∞ definovan². U₧ ne tak jasnΘ bude °eÜenφ. M∙₧ete si zkusit vykreslovat vÜe nebo jen n∞jak primitivn∞ zjiÜ¥ovat, zda-li je danΘ polφΦko vid∞t Φi nikoliv (nap°φklad testem na ka₧dΘ polφΦko), ale v²sledek bude pomal² prßv∞ dφky tomuto testu, proto₧e i v²konn²m procesor∙m chvilku trvß ne₧ zpracujφ 131072 podmφnek. Nakonec byste metodou pokus-omyl doÜli k zßv∞ru, ₧e je lepÜφ vykreslovat vÜe. Metoda quadtree slou₧φ k velice efektivnφmu rozpoznßvßnφ viditeln²ch polygon∙ a o to nßm jde! ╚φm efektivn∞jÜφ algoritmus pou₧ijete, tφm lΘpe. Velice toti₧ usnadnφte prßci procesoru a poslΘze i grafickΘ kart∞.
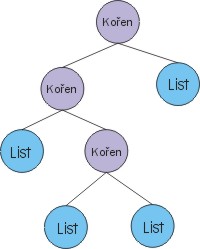
Znßte-li binßrnφ stromy, bude pro Vßs pochopenφ nßsledujφcφ lßtky hraΦkou. Pokud jste se se stromy jeÜt∞ v∙bec nesetkali, mohu vßm slφbit, ₧e podrobn∞ budou probφrßny v serißlu o Datov²ch strukturßch. Zde si ukß₧eme jen zßkladnφ princip strom∙. ZaΦneme u binßrnφho stromu. Binßrnφ strom vypadß n∞jak takto:

Ka₧d² ko°en-rodiΦ mß dva svΘ potomky-listy. Jak bychom oΦekßvali, quadtree bude mφt potomky Φty°i:
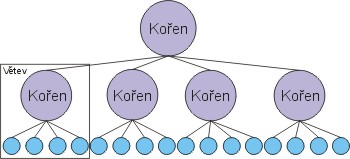
VÜechny modrΘ kuliΦkou jsou listy. List je prvek, kter² nemß dalÜφ potomky. V∞tev je Φßst stromu, kterß obsahuje ko°en a p°φsluÜnΘ listy. Strom, kter² je vyvß₧en² neobsahuje ₧ßdnΘ ko°eny, kterΘ by m∞ly mΘn∞ jak Φty°i potomky. Na v²Üe uvedenΘm obrßzku vidφte vyvß₧en² quadtree (jeÜt∞ v²Üe binßrnφ strom je upadl² doleva). Pokud chceme najφt specifick² list, najdeme ho velice rychle a jednoduÜe. Ka₧dΘho ko°enu se zeptßme, zda-li po₧adovan² list obsahuje nebo ne. Pokud ne, dßle se s v∞tvφ stromu v∙bec nezab²vßme (v∞tÜinou vÜem prvk∙m stromu p°i°azujeme n∞jakΘ ohodnocenφ). U tohoto jednoduchΘho stromu najdeme prvek poka₧dΘ stejn∞ rychle, ale u slo₧it∞jÜφ struktury zaΦne rychlost rapidn∞ nar∙stat.
Podφvßme-li se na nßÜ p°φpad terΘnu, zaΦφnß b²t °eÜenφ pon∞kud jasn∞jÜφ. Nejprve rozd∞lφme naÜe polφΦka do skupin, kterΘ budou tvo°it jednotlivΘ ko°eny stromu, a₧ v nejni₧Üφ vrstv∞ to budou listy. Od shora budeme projφ₧d∞t ko°eny a budeme zkoumat jestli tento ko°en je vid∞t (t°eba i ΦßsteΦn∞). Pokud ne, v∙bec se s touto v∞tvφ dßle zab²vat a p°esuneme se dßl. Celou plochu tedy rozd∞lφme na ko°eny a listy nßsledovn∞:
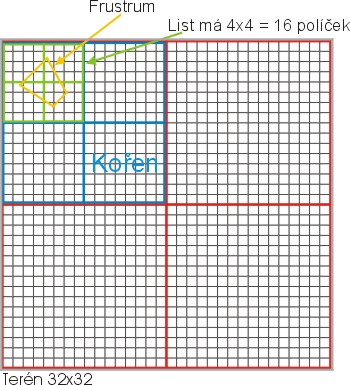
Pro jednoduchost jsem zvolil terΘn 32x32, ale v praxi to funguje na terΘn, u kterΘho m∙₧ete cyklicky d∞lit rozm∞r dv∞ma, krom∞ listu (tam ji₧ nenφ pot°eba d∞lit). Tak₧e nap°φklad pokud se rozhodnete ud∞lat list 5x5, musφ mφt terΘn rozm∞ry 10x10, 20x20, 40x40 atd. NejmenÜφ ΦtvereΦek na obrßzku p°edstavuje skuteΦnΘ polφΦko terΘnu slo₧enΘ nap°φklad ze dvou troj·helnφk∙. Vn∞jÜφ Üed² okraj p°edstavuje hlavnφ ko°en stromu. V tomto ko°enu se frustrum nachßzφ v₧dy, tak₧e tento prvek nemusφme ani testovat (v celkovΘm souΦt∙ test∙ se tento ztratφ). Dßle budeme testovat ka₧d² Φerven∞ ohraniΦen² ko°en. Otestujeme prvnφ a zjistφme, ₧e frustrum se nachßzφ v n∞m. Frustrum by ale mohlo b²t na rozhranφ vφce ko°en∙, tak₧e musφme otestovat i zbylΘ ko°eny na stejnΘ ·rovni. V naÜem p°φpad∞ jsme ale vylouΦili tφmto testem t°i ko°eny, co₧ je dohromady 768 polφΦek z celkov²ch 1024. To je sluÜnΘ, ₧e? PokraΦujeme na dalÜφ ·rovni tentokrßt modr²ch ko°en∙. Zde provedeme zcela analogicky totΘ₧ a vylouΦφme dalÜφch 192 polφΦek (dohromady: 960 polφ). Nakonec testujeme zelenΘ listy a zjistφme, ₧e frustrum se nachßzφ ve vÜech t∞chto listech. Z toho plyne, ₧e musφme vykreslit tyto Φty°i listy. Tak₧e jsme nakonec pouh²mi 9-ti testy zjistili, ₧e 960 polφΦek je mimo frustrum. Jak je vid∞t, testovßnφ Φty° potomk∙ danΘho listu je v₧dy stejnΘ, jen se pracuje poka₧dΘ s jin²m rodiΦem. Zde se tedy dß s v²hodou vyu₧φt rekurzivnφ volßnφ funkce, kterΘ se spustφ poka₧dΘ na vÜechny potomky ka₧dΘho viditelnΘho ko°enu. Data viditeln²ch list∙ se ulo₧φ do vykreslovacφ fronty (nebo p°φmo do dynamickΘho vertex bufferu) a v nßsledujφcφm kroku se vykreslujφ.
V praxi pak zßle₧φ jak velkΘ mßme listy a jak hlubok² je strom - hloubka stromu = poΦet pater. ╚φm v∞tÜφ zvolφte listy, tφm vφce se bude vykreslovat zbyteΦn²ch polygon∙ mimo frustrum, ale zase bude rychlejÜφ rozpoznßvßnφ, proto₧e strom bude mφt mΘn∞ pater. P°edstavte si extrΘm, kdy jako list zvolφme celou plochu. Rozpoznßvßnφ je pak zcela p°eskoΦeno, ale dostali bychom se do p°φpadu z ·vodu, kdy jsou vykreslovßna vÜechna polφΦka Pokud bychom zvolili druh² extrΘm a jako list bychom zvolili pouze jedno polφΦko, budeme mφt jistotu, ₧e se vykreslujφ jen ty polφΦka, kterΘ jsou skuteΦn∞ vid∞t, ale rozpoznßvßnφ zde bude pomalejÜφ. V praxi je proto dobrΘ zvolit vhodn² kompromis mezi ob∞ma extrΘmy, Φasto se m∙₧ete takΘ rozhodnout podle v²konu procesoru nebo grafickΘ karty. V²konnou grafickou kartu pßr polφΦek navφc nezabije, ale pro pomal² procesor m∙₧e b²t "hlubÜφ" rozpoznßvßnφ tvrd² o°φÜek. Rozhodn∞ nenφ dobrΘ spolΘhat na to, ₧e cφlov² u₧ivatel mß dostateΦn∞ v²konnou kartu, kterß zvlßdne vykreslit cel² terΘn s 30FPS (co₧ tedy stejn∞ nic moc) a optimalizaci zcela p°eskoΦit. M∙₧ete se pozd∞ji rozhodnout, ₧e polφΦko sestavφte z vφce troj·helnφk∙ a v²kon vßm rapidn∞ klesne!
Princip metody quadtree mßme za sebou. P°φÜt∞ si ukß₧eme, jak vypadß konkrΘtnφ implementace.
Na zßv∞r si jen ve zkratce popφÜeme metody OctTree. Jak nßzev napovφdß, op∞t se bude jednat o n∞jak² strom. Tentokrßt to bude strom, kde ka₧d² ko°en bude mφt 8 potomk∙. ProΦ zrovna 8? NestaΦφ 4? Mo₧nß jste si vÜimli, ₧e v p°φpad∞ quadtree jsme d∞lili terΘn pouze v rovin∞, nynφ budeme d∞lit v prostoru a prßv∞ proto je pot°eba 8 list∙. Ji₧ se nebude jednat o Φtverce, ale o krychle. UrΦφme si tedy zßkladnφ krychli, kterß obepφnß cel² terΘn (m∙₧e se jednat obecn∞ o kvßdr) a tu pak rozd∞lφme na 8 menÜφch krychliΦek. Ka₧dou tuto malou krychliΦku op∞t rozd∞lφme na 8 jeÜt∞ menÜφch krychliΦek, a₧ se dostaneme na ·rove≥ list∙ a d∞lenφ p°eruÜφme.
Princip rozpoznßvßnφ viditeln²ch polygon∙ je analogick² metod∞ quadtree. Nejprve se podφvßme, zda-li je frustrum v prvnφ nejv∞tÜφ krychli, tam bude asi urΦit∞ (pokud nenφ kamera otoΦenß na druhou stranu), dßle testujeme vÜech 8 podkrychliΦek a vybereme jen ty, kterΘ jsou ve frustrum. S ostatnφmi se v∙bec nezab²vßme.
ProΦ tedy d∞lit zbyteΦn∞ prostor na vφce oddφl∙? Ano, rozpoznßvßnφ viditeln²ch krychlφ bude pravd∞podobn∞ pomalejÜφ ne₧ v p°φpad∞ metody quadtree. Ale p°edstavme si m∞sto typu NY, kde je hodn∞ mrakodrap∙ a kdy₧ jsme s kamerou hodn∞ blφzko nad povrchem, nemusφ b²t viditelnΘ mrakodrapy vid∞t celΘ, jin²mi slovy uvidφme jen malou Φßst a proΦ tedy zbyteΦn∞ vykreslovat cel² mrakodrap (tzn. i jeho nejvyÜÜφ patra), kdy₧ jsme n∞kde u jeho paty? Pomocφ metody octree rozd∞lφme mrakodrapy i v horizontßlnφm sm∞ru a tudφ₧ se vykreslφ p°esn∞ to, co je vid∞t (a mo₧nß patro navφc). V tom je hlavnφ v²hoda tΘto metody, vykoupenß slo₧it∞jÜφ implementacφ (aΦkoliv to je dost relativnφ) a mo₧nß vyÜÜφ Φasovou slo₧itostφ vyhledßvßnφ viditeln²ch krychlφ.
Na zßv∞r tΘto Φßsti se podφvßme na jednoduch² obrßzek, kter² nßm osv∞tlφ princip metody octree. Vidφme, ₧e hlavnφ krychle je rozd∞lena na 8 menÜφch a ty d∞lφ nßÜ "vysok²" objekt. Pokud tedy kamera bude nasm∞rovanß ve sm∞ru Üipky, bude se vykreslovat pouze krychle, kterß je vzadu a vlevo a z toho vypl²vß, ₧e o hornφ Φßst objektu se nebudeme v∙bec starat!
Ji₧ jsem zmφnil, ₧e v p°φÜtφ lekci se budeme v∞novat implementaci algoritm∙ quadtree. Tak₧e si vytvo°φme jednoduchou plochu a na nφ si budeme testovat r∙znΘ postupy vykreslovßnφ jednotliv²ch polφΦek.
T∞Üφm se p°φÜt∞ nashledanou.