V poslednφm dφlu jsme ukonΦili povφdßnφ o datov²ch strukturßch, kterΘ byly implementovßny p°es pole, co₧ nßs v n∞kter²ch ohledech omezovalo. Dnes se zaΦneme v∞novat datovΘ struktu°e seznamu, kterß je zalo₧ena na dynamickΘ alokaci pam∞ti.
Sice u₧ jsme se seznamem pracovali, ale neuvedli jsme si jeho charakteristickΘ vlastnosti:
pevn∞ stanovenΘ po°adφ
mo₧nost opakovßnφ stejn²ch prvk∙
mo₧nost uklßdat, vyjφmat a samoz°ejm∞ vyhledßvat ·daje
NßÜ seznam (a¥ u₧ pole, fronta nebo zßsobnφk) implementovan² pomocφ polφ byl statick², museli jsme tedy u₧ p°φmo v programu urΦit kolik bude mφt maximßln∞ prvk∙. Toto omezenφ odstranφme vyu₧itφm spojovΘho seznamu, jeho₧ jednotlivΘ prvky jsou vytvß°eny p°φmo za b∞hu programu. Proto₧e alokace pam∞ti probφhß p°φmo za b∞hu programu, mß jistΘ nev²hody. Za prvΘ je pam∞¥ov∞ nßroΦn∞jÜφ, proto₧e ka₧d² prvek musφ obsahovat ukazatel na dalÜφ prvek (nßsledovnφka, pop°. i p°edch∙dce) a funkce pro alokaci pam∞ti nepat°φ k funkcφm, kterΘ by byly zrovna mßlo Φasov∞ nenßroΦnΘ. Druhou nev²hodou pak je, ₧e na k-t² prvek se m∙₧eme dostat pouze pr∙chodem p°es prvky le₧φcφ p°ed nφm (nebo za nφm, pokud je obousm∞rn²) nelze pou₧φt v²hod indexovßnφ jako u polφ. Poslednφ pak je, ₧e je trochu nßroΦn∞jÜφ pro implementaci.
My se nynφ budeme v∞novat lineßrnφmu spojovΘmu seznamu a to konkrΘtn∞ jednosm∞rnΘmu - ka₧d² prvek bude obsahovat ukazatel pouze na svΘho nßsledovnφka.
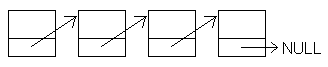
Je to tedy posloupnost objekt∙ (struktur, t°φd) stejnΘho typu, kterΘ jsou se°azeny do °ady. Jeho funkce je podobnß funkci jednorozm∞rnΘho pole, ovÜem ji₧ s v²Üe uvedenou nev²hodou: nejde indexovat, prochßzφme tedy v₧dy od zaΦßtku. Grafickß reprezentace tΘto datovΘ struktury:
Malß spodnφ Φßst prvku zobrazuje datov² prvek obsa₧en² ve struktu°e, kter² odkazuje na nßsledujφcφ prvek. Velkß Φßst pak zobrazuje data. Seznam je ukonΦen prvkem, ve kterΘm jsou platnß data, ale ukazatel na dalÜφ prvek mß hodnotu NULL. Druhou mo₧nostφ je zarß₧ka, se kterou se setkßme my. Zarß₧ka neobsahuje data vklßdanß u₧ivatelem, uvidφme jak se ale dß vyu₧φt pro ulehΦenφ n∞kter²ch operacφ:
Implementovat budeme dv∞ t°φdy a to t°φdu CJednPrvek, kterß bude, jak u₧ nßzev °φkß, prvkem jednosm∞rnΘho lineßrnφho spojovΘho seznamu. Druhou t°φdou bude CLinSpojSeznam, obsahujφcφ jako Φlenskou prom∞nnou typu CJednPrvek urΦujφcφ zaΦßtek seznamu. Proto₧e do seznamu budeme jist∞ p°idßvat prvky, tak se nßm bude hodit i prom∞nnß ukazujφcφ na jeho konec. Pokud by tam nebyla, tak bychom p°i ka₧dΘm vlo₧enφ prvku na konec seznamu museli projφt cel² seznam (tedy vÜech N prßv∞ ulo₧en²ch prvk∙):
#ifndef LINSPOJSEZNAM_H
#define LINSPOJSEZNAM_H
template<class T> class CJednPrvek {
private:
T m_Data;
CJednPrvek<T> *m_lpDalsi;
public:
CJednPrvek() : m_lpDalsi(NULL) { }
CJednPrvek(const T& _Data) : m_Data(_Data), m_lpDalsi(NULL) { }
T VratData() const { return m_Data; }
CJednPrvek<T>* VratDalsi() const { return m_lpDalsi; }
void NastavDalsi(CJednPrvek<T> *_lpDalsi) { m_lpDalsi = _lpDalsi; }
void NastavData(const T& _Data) { m_Data = _Data; }
};
template<class T> class CLinSpojSeznam {
private:
CJednPrvek<T> *m_lpPrvni, *m_lpPosledni;
public:
CLinSpojSeznam() : m_lpPrvni(NULL), m_lpPosledni(NULL) { }
~CLinSpojSeznam() { if(!JePrazdny()) { SmazSeznam(); } }
bool VytvorPrazdny();
bool SmazSeznam();
bool JePrazdny() { return (m_lpPrvni == m_lpPosledni); }
bool VlozNaKonec(const T& _Data);
// vklada na konec seznamu
void Vypis();
};
T°φda CJednPrvek je jasnß, zapouzd°uje pouze nßÜ datov² prvek a ukazatel na dalÜφ objekt CJednPrvek. T°φda CLinSpojSeznam pak pro zaΦßtek obsahuje metody pro zßkladnφ prßci se seznamem, slo₧it∞jÜφ metody budeme p°idßvat postupn∞:
template<class T> bool CLinSpojSeznam<T>::VytvorPrazdny()
{
bool bNavrat = false;
m_lpPrvni = new CJednPrvek<T>; // konstruktor automaticky nastavi m_lpDalsi na NULL,
jinak bychom to museli udelat my
if(m_lpPrvni)
{
m_lpPosledni = m_lpPrvni; // zacatek je i koncem
bNavrat = true;
}
return bNavrat;
}
K tomuto kousku k≤du je nutnΘ dodat, ₧e aΦkoliv vytvß°φme prßzdn² seznam, obsahuje tento hned jeden prvek. Tento specißlnφ prvek budeme naz²vat zarß₧kou a s v²hodou ji vyu₧ijeme p°i prochßzenφ pole za ·Φelem nalezenφ prvku s urΦitou hodnotou. Na tento prvek bude v₧dy ukazovat Φlenskß prom∞nnß t°φdy CLinSpojSeznam::m_lpPosledni. Proto₧e prßzdn² seznam je celkem k niΦemu, ukß₧eme si jak ulo₧it prvek na konec seznamu:
template<class T> bool CLinSpojSeznam<T>::VlozNaKonec(const
T& _Data)
{
bool bNavrat = false;
if(m_lpPosledni) // pokud existuje zarazka
{
// vytvorime novy konec (prazdny prvek)- musime dynamicky
CJednPrvek<T> *lpNovy= new CJednPrvek<T>;
// ulozime data do posledniho prvku -
zarazky
m_lpPosledni->NastavData(_Data);
m_lpPosledni->NastavDalsi(lpNovy);
m_lpPosledni = lpNovy; // poslednim prvkem je nove vytvorena zarazka
bNavrat = true;
// pozor prvek novy zde nesmime uvolnit !!!
}
return bNavrat;
}
Zde vyu₧ijeme toho, ₧e poslednφ prvek je zarß₧ka, kterß neobsahuje pro nßs zajφmavß data. Ulo₧φme tedy data p°edanß jako parametr do tΘto zarß₧ky a vytvo°φme nov² prßzdn² prvek - novou zarß₧ku. Alokaci provedeme dynamicky, proto₧e staticky alokovan² prvek by zanikl po zavolßnφ p°φkazu return. PotΘ nastavφme ukazatel v p∙vodnφ zarß₧ce tak, aby ukazoval na nov∞ vytvo°enou zarß₧ku a koneΦn∞ posuneme ukazatel na zarß₧ku na nov² konec. Toto vÜe provedeme jen za p°edpokladu, ₧e existuje zarß₧ka, tedy seznam byl korektn∞ vytvo°en. Nynφ si ukß₧eme funkci pro v²pis seznamu:
template<class T> void CLinSpojSeznam<T>::Vypis()
{
cout << "Stav seznamu: ";
if(!JePrazdny())
{
CJednPrvek<T> *lpVypisovany= m_lpPrvni;
while(lpVypisovany!= m_lpPosledni) // data zarazky pro nas nejsou dulezita
{
cout << lpVypisovany->VratData() << " ";
lpVypisovany= lpVypisovany->VratDalsi();
}
}
else
{
cout << " PRAZDNY";
}
cout << endl;
}
Pokud seznam nenφ prßzdn² (tedy ukazatele m_lpPrvni a m_lpPosledni jsou r∙znΘ), vyu₧ijeme cyklu while a pomocnΘ prom∞nnΘ vypisovany k vypsßnφ obsahu vÜech prvk∙, samoz°ejm∞ krom∞ zarß₧ky. A proto₧e jsme alokovali dynamicky pam∞¥, musφme sezname korektn∞ zruÜit:
template<class T> bool CLinSpojSeznam<T>::SmazSeznam()
{
bool bNavrat = false;
if(!JePrazdny())
{
CJednPrvek<T> *lpMazany;
while(m_lpPrvni)
{
lpMazany= m_lpPrvni;
m_lpPrvni = m_lpPrvni->VratDalsi();
// posun na dalsi prvek
delete lpMazany;
}
bNavrat = true;
}
return bNavrat;
}
Seznam uvolnφme pr∙chodem od zaΦßtku
postupn²m odmazßvßnφm prvk∙ v po°adφ, ve kterΘm byly ulo₧eny do seznamu. Tφm
mßme naÜi zßkladnφ kostru, kterou budeme dßle rozÜi°ovat o u₧iteΦnΘ funkce. Nejprve
vyhledßvßnφ prvku:
template<class T> CJednPrvek<T>* CLinSpojSeznam<T>::Najdi(const
T& _Data)
{
CJednPrvek<T> *lpNavrat = NULL; // implicitne nenalezeno
if(!JePrazdny())
{
CJednPrvek<T> *lpZkoumany= m_lpPrvni;
m_lpPosledni->NastavData(_Data); // ulozime data do zarazky
while(lpZkoumany->VratData() != _Data)
{
lpZkoumany= lpZkoumany->VratDalsi();
}
if(lpZkoumany!= m_lpPosledni)
{
lpNavrat =
lpZkoumany; // nalezli jsme prvek
}
}
return lpNavrat;
}
Zde jsme s v²hodou vyu₧ili zarß₧ky, do kterΘ ulo₧φme hledanou hodnotu. Potom mßme jistotu, ₧e tuto hodnotu nalezneme v₧dy a nemusφme se zab²vat tφm, jestli jsme dosßhli konce seznamu. Ukß₧eme si, jak by vypadala metoda p°epsanß pro ov∞°ovßnφ konce pole:
template<class T> CJednPrvek<T>* CLinSpojSeznam<T>::NajdiBezZarazky(const
T& _Data)
{
CJednPrvek<T> *lpNavrat = NULL; // implicitne nenalezeno
if(!JePrazdny())
{
CJednPrvek<T> *lpZkoumany= m_lpPrvni;
while(lpZkoumany!= m_lpPosledni )
{
if(_Data == lpZkoumany->VratData())
{
lpNavrat = lpZkoumany;
break; //
preruseni cyklu
}
lpZkoumany= lpZkoumany->VratDalsi();
// posun na dalsi prvek
}
}
return lpNavrat;
}
Vidφme, ₧e zarß₧ka je velice u₧iteΦnß v∞c. UÜet°φme si toti₧ nejen problΘmy s pracφ s ukazateli, ale uÜet°φme si tΘ₧ ov∞°ovßnφ podmφnky na platnost ukazatele v ka₧dΘm kroku. Ob∞ tyto metody vracφ pouze prvnφ v²skyt danΘho prvku. P°idßnφm parametru typu unsigned integer a jednoduchou ·pravou metody bez zarß₧ky lze upravit hledßnφ pro nalezenφ k-tΘho prvku. Ukß₧eme si verzi bez zarß₧ky:
template<class T> CJednPrvek<T>* CLinSpojSeznam<T>::Najdi(const
T& _Data, unsigned int _k)
{
CJednPrvek<T> *lpNavrat = NULL; // implicitne nenalezeno
if(!JePrazdny())
{
CJednPrvek<T> *lpZkoumany= m_lpPrvni;
while((lpZkoumany!= m_lpPosledni) && (_k != 0))
{
if(_Data == lpZkoumany->VratData())
{
if(--_k == 0)
{
lpNavrat = lpZkoumany;
break;
}
}
lpZkoumany= lpZkoumany->VratDalsi();
}
}
return lpNavrat;
}
V tomto p°φpad∞ je u₧itφ zarß₧ky slo₧it∞jÜφ. Nynφ metoda pro vlo₧enφ dat na zaΦßtek lineßrnφho spojovΘho seznamu:
template<class T> bool CLinSpojSeznam<T>::VlozNaZacatek(const
T& _Data)
{
bool bNavrat = false;
if(m_lpPrvni) // pokud je pred co vkladat
{
CJednPrvek<T> *lpNovy = new CJednPrvek<T>(_Data);
if(lpNovy)
{
lpNovy->NastavDalsi(m_lpPrvni); // novy prvek bude ukazovat na puvodni zacatek
m_lpPrvni = lpNovy; // a posuneme novy zacatek
bNavrat = true;
}
// opet novy prvek nemazeme !!!
}
return bNavrat;
}
#endif
Pouze vytvo°φme nov² prvek a zapojφme zep°edu do seznamu a upravφme ukazatel na prvnφ prvek.
Pro dneÜek jsme si ukßzali zßkladnφ operace pro prßci s lineßrnφm spojov²m seznamem, v p°φÜtφm dφlu p°idßme dalÜφ metody. Jak bylo slφbeno v dφlech v∞novan²ch front∞ a zßsobnφku, povφme si jak implementovat tyto dv∞ datovΘ struktury pomocφ lineßrnφho spojovΘho seznamu. Implementovat budeme takΘ frontu obousm∞rnou. A mo₧nß u₧ p°φÜt∞ si povφme n∞co o dynamicky vytvß°en²ch stromech.
PřφÜtě nashledanou.