V dneÜnφm pokraΦovßnφ se jeÜt∞ vrßtφme k p°et∞₧ovßnφ operßtor∙ a to konkrΘtn∞ k operßtor∙m new a delete. Potom se vrßtφme k tomu, co jsme naΦali minule, tedy d∞diΦnosti. Povφme si n∞co o jednoduchΘ d∞diΦnosti a vÜe si ukß₧eme na p°φkladech.
Jak ji₧ vφme operßtory new a delete slou₧φ k alokaci a uvoln∞nφ dynamicky alokovanΘ pam∞ti. Oba operßtory existujφ ve dvou verzφch a to operßtor pro jednoduchΘ prom∞nnΘ:
void* operator new(size_t _velikost);
a pak je tu operßtor, kter² je urΦen pro alokace polφ:
void* operator new[](size_t _velikost);
Pou₧itφm operßtoru new dojde prßv∞ na zßklad∞ druhu prom∞nnΘ, pro kterou chceme alokovat pam∞¥ k zavolßnφ jednΘ z t∞chto funkcφ. Operßtor delete mß takΘ dv∞ verze:
void operator delete(void *ptr);
, resp. pro pole:
void operator delete[](void *p);
Je vhodnΘ poznamenat, ₧e operßtor new se starß pouze o alokaci pam∞ti, tedy nap°. volßnφ konstruktoru je starostφ p°ekladaΦe. Stejn∞ tak i volßnφ destruktoru v p°φpad∞ operßtoru delete. Jak ji₧ vφme, operßtor new v p°φpad∞, ₧e nenφ dostatek pam∞ti pro uspokojenφ po₧adavku, vracφ NULL. Jinou reakcφ na nedostatek pam∞ti m∙₧e b²t vyvolßnφ v²jimky, ale t∞mi se budeme zab²vat a₧ v n∞kterΘm z nßsledujφcφch dφl∙.
Narozdφl od ostatnφch operßtor∙ lze tyto dva operßtory krom∞ p°etφ₧enφ i p°edefinovat, Φφm₧ dojde k nahrazenφ standardnφch verzφ po celou dobu b∞hu programu. Jednφm z d∙vod∙ pro p°edefinovßnφ t∞chto operßtor∙ m∙₧e b²t pot°eba ov∞°enφ, zdali sprßvn∞ uvol≥ujeme pam∞¥ nebo inicializace bloku pam∞ti p°edem zadanou hodnotou. Mohli bychom takΘ v operßtorovΘ funkci new zv∞tÜit o mal² kousek alokovan² ·sek, kter² bychom vyplnili p°edem zadanou hodnotou a p°i uvol≥ovßnφ bychom tento ·sek mohli zkontrolovat. Pokud by byl zm∞n∞n, pak pravd∞podobn∞ doÜlo k necht∞nΘmu p°φstupu do pam∞ti, kterß nßm u₧ nepat°φ. V ukßzce bude program p°i provedenφ alokace vypisovat kolik byte pam∞ti si u₧ivatel p°eje p°id∞lit a p°i uvoln∞nφ pak vypφÜe adresu bloku pam∞ti, kter² se uvol≥uje:
#include "stdafx.h"
// Pouzivame predkompilovane hlavicky
#include <stdio.h>
#include <malloc.h>
#include <iostream.h>
void* operator new(size_t _velikost)
{
void* p = NULL;
printf("Pokus o alokaci %u byte ... ", _velikost);
if(!_velikost) { _velikost = 1; } // operator new by mel vracet ruzne
adresy
p = malloc(_velikost);
if(p)
{
printf("uspesne (adresa : %p)\n", p);
}
else
{
printf("neuspesne\n");
}
return p;
}
void operator delete(void* _ptr)
{
printf("Dealokace bloku na adrese %p\n", _ptr);
if(_ptr)
{
free(_ptr);
}
}
int main(int argc,
char* argv[])
{
int i = 0;
int *p_int;
p_int = new int;
*p_int = i;
int *p_int2;
p_int2 = new int[4096];
delete p_int2;
delete p_int;
char c;
cin >> c;
return 0;
}
Zdrojov² k≤d naleznete v sekci Downloads (projekt PretNew).
U standardnφho operßtoru new je v dokumentaci uvedeno, ₧e v p°φpad∞ opakovanΘ alokace 0 byte operßtor new vracφ ukazatele na r∙znΘ oblasti pam∞ti. To mßme nynφ zajiÜt∞no alokacφ 1 byte. Tedy i kdy₧ u₧ivatel chce (spφÜe ale nechce) blok pam∞ti, vrßtφme mu jeden byte.
Pokud se rozhodneme, ₧e se nßm funkce printf() nelφbφ a nahradφme ji volßnφm cout dostaneme se do potφ₧φ. Tento objekt toti₧ intern∞ pou₧φvß operßtory new a delete k alokovßnφ a uvoln∞nφ bloku pomocnΘ pam∞ti. AvÜak nßmi definovan² operßtor nahradil standardnφ verzi, Φφm₧ dojde k rekurzivnφmu volßnφ funkce, kterΘ ale chybφ ukonΦovacφ podmφnka. Tφm m∙₧e u n∞kter²ch implementacφ vzniknout nekoneΦn² cyklus.
Kv∙li v²Üe uvedenΘmu se tedy redefinici operßtor∙ new a delete na globßlnφ ·rovni sna₧φme vyhnout. Pou₧ijeme tedy mo₧nosti p°etφ₧enφ operßtoru new jako metody n∞jakΘ t°φdy nebo jako globßlnφho operßtoru s p°idan²mi parametry, kdy se m∙₧eme rozhodnout jestli pou₧ijeme naÜφ verzi nebo standardnφ:
void* operator new(size_t
_velikost, int _iMuj)
{
printf("Toto je muj operator new");
return operator new(_velikost);
}
int main(int argc, char* argv[])
{
int *p_int;
p_int = new(5) int; // Dojde k zavolani naseho operatoru new
delete p_int;
return 0;
}
Zdrojov² k≤d naleznete v sekci Downloads (projekt PretNew2).
Podobn∞ jako jsme p°et∞₧ovali operßtory new a delete bychom mohli p°etφ₧it jejich verze pro pole, operßtory new[] a delete[]. Ve v∞tÜin∞ p°φpad∙ je to vÜak zbyteΦnΘ, nebo¥ tyto operßtory intern∞ pou₧φvajφ operßtor∙ new a delete.
Nynφ si ukß₧eme jak p°etφ₧it operßtor pro t°φdu:
#include "stdafx.h"
// Pouzivame predkompilovane hlavicky
#include <stdlib.h>
#include <memory.h>
#include <iostream.h>
class Test {
public:
void *operator new(size_t _velikost, char _cznak);
char VratZnak() { return m_cZnak; }
private:
char m_cZnak;
};
void* Test::operator new(size_t _velikost, char _cZnak)
{
void *p = malloc(_velikost);
if(p)
{
memset(p, _cZnak, _velikost);
}
return p;
}
int main(int argc, char* argv[])
{
Test *cTest = new('G') Test;
cout << "Znak je : " << cTest->VratZnak() << endl;
char c;
cin >> c;
return 0;
}
P°i alokaci pam∞ti cel² ·sek nastavφme na zadanou hodnotu. Globßlnφ operßtor new je p°ed touto t°φdou skryt, tak₧e p°φkaz:
Test *cTest = new Test;
vyvolß chybu p°i p°ekladu. Pokud bychom ovÜem pot°ebovali pro alokaci pou₧φt standardnφho operßtoru new, pom∙₧e nßm nßsledujφcφ °ßdek:
Test *cTest = ::new Test;
P°etφ₧φme-li operßtory new a delete jako metody objektovΘho typu, jsou v₧dy statickΘ. A to i v p°φpad∞, ₧e klφΦovΘ slovo static neuvedeme.
Zdrojov² k≤d naleznete v sekci Downloads (projekt PretNew3).
JeÜt∞ se podφvßme na zvlßÜtnφ operßtor new, kter² je v souboru new.h. Je definovßn takto:
void* operator new(size_t
_velikost, void* p)
{
return p;
}
Jak vidφme, tak tento operßtor ve svΘm t∞le neobsahuje ₧ßdnΘ p°φkazy pro alokaci bloku pam∞ti. K Φemu se tedy vlastn∞ hodφ? Podφvejme se na nßsledujφcφ p°φklad:
#include "stdafx.h"
// Pouzivame predkompilovane hlavicky
#include <iostream.h>
void* operator new(size_t _velikost, void *_p)
{
return _p;
}
void operator delete(void *_ptr, void *_p2)
{
;
}
class Test
{
private:
char a, b;
public:
Test() { a = 'A'; b = 'B'; }
};
char pole[64];
int main(int argc, char* argv[])
{
// Zinicializujeme na X
for(int i = 0; i < 64; i++)
{
pole[i] = 'X';
}
Test *mujtest = new(pole) Test;
cout << "Adresa pole je : " << &pole << endl;
cout << "Adresa objektu je : " << mujtest << endl;
for(i = 0; i < 64; i++)
{
cout << pole[i];
}
char c;
cin >> c;
return 0;
}
Zdrojov² k≤d naleznete v sekci Downloads (projekt PretNew4).
Na v²stupu programu pak uvidφme, ₧e se adresy pro pole znak∙ a instanci t°φdy Test shodujφ. Takto definovan² operßtor tedy jen vrßtφ ukazatel na zadanou adresu. Pokud si pak vypφÜeme obsah pole, uvidφme, ₧e pole ve sv²ch dvou prvnφch bytech obsahuje ΦlenskΘ prom∞nnΘ t°φdy Test. Prßzdn² operßtor delete je uveden, aby p°ekladaΦ nehlßsil upozorn∞nφ, ₧e neexistuje odpovφdajφcφ operßtor delete, kter² by uvolnil pam∞¥ pokud by vznikla p°i inicializaci v²jimka. Pokud chceme definovat odpovφdajφcφ operßtor delete k operßtoru new, pak musφ mφt parametry shodnΘ od druhΘho a p°φpadn∞ v²Üe. Tento operßtor nemusφme vlastnoruΦn∞ p°et∞₧ovat, staΦφ pouze vlo₧it soubor new.h do naÜeho programu.
Jin²m p°φkladem by mohlo b²t p°etφ₧enφ operßtoru new jako metody t°φdy. V programu bychom pak definovali ·sek pam∞ti (pole) pro vytvß°enφ instancφ tΘto t°φdy. Toto pole by mohlo b²t takΘ statickou Φlenskou prom∞nnou danΘ t°φdy. Operßtor new by pak vracel ukazatele do tohoto pole a v ΦlenskΘ statickΘ prom∞nnΘ by si udr₧oval index na zb²vajφcφ volnΘ mφsto v tomto poli. Pokud bychom v tomto poli cht∞li uklßdat i pole objekt∙, tedy pomocφ operßtoru new[], museli bychom ho v tΘto t°φd∞ p°etφ₧it. Jinak by se pou₧il globßlnφ operßtor, kter² by alokoval blok pam∞ti z dostupnΘ volnΘ pam∞ti. Pro alokovßnφ pam∞ti pro t°φdu Test mimo pole (tedy ve volnΘ pam∞ti) lze op∞t pou₧φt globßlnφ operßtor new, kter² musφme kvalifikovat Φty°teΦkou (::).
A koneΦn∞, chceme-li jen alokovat pam∞¥ (bez zavolßnφ konstruktoru) nebo pam∞¥ uvolnit (bez volßnφ destruktoru):
Test *bezvolani = (Test *)operator new(sizeof(Test));
// Pouziti
operator delete(bezvolani);
Zdrojov² k≤d naleznete v sekci Downloads (projekt PretNew5).
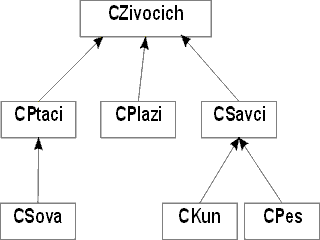
V minulΘm dφle jsme se dov∞d∞li n∞jakΘ obecnΘ informace o d∞diΦnosti. Dnes si ukß₧eme jak pou₧φt jednoduchΘ d∞diΦnosti. ZaΦneme ale pojmem hierarchie t°φd. Slo₧it∞jÜφ programy se neobejdou pouze s jednou t°φdou, mohou jich mφt stovky. P°i pou₧itφ d∞diΦnosti vzniknou p°φbuzenskΘ vztahy mezi n∞kter²mi t°φdami. Tuto strukturu naz²vßme hierarchiφ t°φd. Pro minule uveden² p°φklad se zoologickou zahradou by mohl vypadat nap°φklad takto:
Vidφme, ₧e hierarchie pro jednoduchou d∞diΦnost mß tvar stromu. Libovolnß t°φda, krom∞ zßkladnφ, mß pouze jednoho p°edka. T°φdu na nejvyÜÜφ ·rovni naz²vßme ko°enovou t°φdu (angl. root), je to spoleΦn² prvek pro vÜechny t°φdy v hierarchii. T°φda ze kterΘ vede Φßra je t°φdou odvozenou, t°φda v nφ₧ konΦφ Üipka je t°φdou zßkladnφ. Sm∞r Üipky je zvolen tφmto zp∙sobem, proto₧e odvozenß t°φda znß svou zßkladnφ t°φdu, kde₧to zßkladnφ t°φda nevφ, kterΘ dalÜφ t°φdy z nφ budou odvozeny. Jazyk C++ nßm krom∞ jednoduchΘ d∞diΦnosti umo₧≥uje pou₧φt d∞diΦnost vφcenßsobnou a d∞diΦnost opakovanou. P°i vφcenßsobnΘ d∞diΦnosti mß t°φda vφce rodiΦ∙, v grafu tedy bude ukazovat na vφce t°φd v hierarchii. P°i opakovanΘ d∞diΦnosti, ke kterΘ dochßzφ p°edevÜφm ve slo₧it∞jÜφch hierarchiφch, zd∞dφ t°φda vlastnosti n∞kterΘho p°edka vφce cestami.
M∞jme t°φdu nebo strukturu Predek. Potom t°φdu nebo strukturu Potomek, odvozenou od t°φdy Predek, deklarujeme nßsledovn∞:
class Potomek : Predek {
/*Pridane prvky*/
};
nebo
struct Potomek : Predek {
/*Pridane prvky*/
};
V C++ je struktura vlastn∞ to samΘ co t°φda, s tφm rozdφlem, ₧e vÜechny jejφ prvky jsou implicitn∞ ve°ejnΘ (public). V obou p°φpadech m∙₧eme p°ed jmΘnem t°φdy, od kterΘ d∞dφme uvΘst specifikßtory p°φstupu (public, private, protected). Pokud neuvedeme ₧ßdn² z t∞chto specifikßtor∙ platφ nßsledujφcφ: pokud je d∞d∞n² objekt t°φdou platφ implicitn∞ private, u struktur public. Nßsledujφcφ tabulka ukazuje, jak budou ovlivn∞na p°φstupovß prßva ve zd∞d∞nΘ t°φd∞:
|
p°φstupovΘ prßvo v rodiΦovskΘm objektu |
public |
protected |
private |
|
odvozenφ public |
public |
protected |
nep°φstupn² |
|
odvozenφ protected |
protected |
protected |
nep°φstupn² |
|
odvozenφ private |
private |
private |
nep°φstupn² |
Äe je prvek nep°φstupn² znamenß, ₧e k n∞mu nenφ mo₧no p°istupovat v t∞le metod p°idan²ch do odvozenΘ t°φdy. K p°φstupu k nim je tedy nutnΘ pou₧φt Φlensk²ch metod, jako bychom k nim p°istupovali z vn∞jÜku t°φdy. Chrßn∞nΘ prvky m∙₧eme pou₧φt v nov∞ p°idan²ch metodßch odvozenΘ t°φdy, ale nejsou p°φstupnΘ z venku. Ve°ejnΘ prvky lze op∞t vyu₧φt v nov∞ p°idan²ch metodßch odvozenΘ t°φdy, ale krom∞ toho jsou jeÜt∞ p°φstupnΘ vn∞jÜφm p°φstupem.
Vφme-li, ₧e od danΘ t°φdy budeme chtφt d∞dit a v p°idan²ch metodßch pak p°istupovat k Φlensk²m prom∞nn²m zßkladnφ t°φdy, je nejlepÜφ pou₧φt pro prom∞nnΘ v zßkladnφ t°φd∞ p°φstupovΘho prßva protected a t°φdu zd∞dit pomocφ specifikßtoru p°φstupu public. Vyhneme se tφm zbyteΦnΘmu volßnφ metod zp°φstup≥ujφcφch danΘ prom∞nnΘ a zachovßme pravidlo, ₧e prom∞nnΘ nebudou p°φstupnΘ zvn∞jÜku objektu. V p°φkladech v∞novan²ch d∞diΦnosti budeme v∞tÜinou pou₧φvat prßv∞ tohoto zp∙sobu.
Pokud chceme, m∙₧eme u vybran²ch prom∞nn²ch vrßtit jejich p°φstupovß prßva na ·rove≥ kterou m∞la ve t°φd∞ od nφ₧ odvozujeme. Ukßzka:
class Predek {
public:
char a;
};
class Potomek : Predek {
public:
Predek::a; // Pokud neni uvedeno, prekladac
pri primem pristupu k prvku a ohlasi chybu (public se totiz pri
private dedeni
stane private)
};
To samΘ lze za°φdit pomocφ nov∞jÜφho zßpisu:
class Potomek : Predek {
public:
using Predek::a;
};
Pro zm∞n∞nφ p°φstupovΘho prßva metody je nutnΘ uvΘst v obou p°φpadech metodu bez zßvorek.
Pokud se nßm nezdß vhodnΘ ponechat p°φstup k n∞jakΘ metod∞ rodiΦovskΘ t°φdy, lze ji zakßzat. Provedeme to tak, ₧e v odvozenΘ t°φd∞ deklarujeme soukromou metodu se stejn²m typem a parametry. Tato metoda p∙vodnφ metodu zastφnφ a tφm znemo₧nφ jejφ pou₧itφ vn∞ t°φdy. V p°φpad∞, ₧e bychom ji cht∞li zavolat uvnit° n∞jakΘ ΦlenskΘ funkce musφme ji zavolat jejφm cel²m jmΘnem, tedy nap°. Predek::Metoda().
Existujφ takΘ prvky, kterΘ se ned∞dφ. Ned∞dφ se konstruktor. Jeho volßnφ za°φdφ p°ekladaΦ, pop°φpad∞ ho lze v konstruktoru odvozenΘ t°φdy zavolat explicitn∞. Podobn∞ se ned∞dφ destruktor, ale je op∞t vyvolßn p°ekladaΦem. A takΘ se ned∞dφ p°etφ₧en² operßtor operator=(). Pokud nenφ explicitn∞ definovßn pro odvozenou t°φdu, vyu₧ije se operßtor p°edka p°i konstrukci implicitnφho p°i°azovacφho operßtoru potomka.
P°φÜt∞ se podφvßme podrobn∞ji na volßnφ konstruktor∙ a destruktor∙ v odvozen²ch t°φdßch. Dßle virtußlnφmu d∞d∞nφ, virtußlnφm metodßm a abstraktnφm t°φdßm.
PřφÜtě nashledanou.
