Kurz C++ (9.)

┌vod do OOP

Vφtßm Vßs na dalÜφm pokraΦovßnφ kurzu o C++. Vlastn∞ a₧ ode dneÜka si kurz zaslou₧φ nßzev "o C++", proto₧e do te∩ jsme se v∞novali jazyku C a rozÜφ°enφm, kterΘ p°inesl jazyk C++, ale objekt∙m (co₧ je nejv∞tÜφ p°φnos jazyka C++ oproti jazyka C) jsme se nev∞novali, ale to dnes napravφme – zaΦneme pronikat do taj∙ OOP, tedy objektov∞ orientovanΘho programovßnφ.

ProΦ OOP

Programovßnφ, kterΘmu jsme se v∞novali do dnes, se °φkß imperativnφ. Program je prost∞ sled instrukcφ (volßnφ funkcφ a p°φkaz∙ jazyka), kter² b∞hß v n∞jakΘm pevn∞ danΘm po°adφ. Ale to nenφ vÜe, navφc jsme p°ed∞lali problΘmy, kter² jsme °eÜili, na jinΘ, jejich₧ struktura by vφce odpovφdala struktu°e poΦφtaΦe. P°φkladem nßm m∙₧e b²t op∞t adresß° osob. Adresß° jsme naprogramovali jako strukturu obsahujφcφ data (pole jmen a telefonnφch Φφsel), ale operace s touto strukturou (kterΘ jsou s nφ neodd∞liteln∞ spjaty - vyhledßvßnφ jmΘna, p°idßnφ atd.) jsme odd∞lili a implementovali jako vn∞jÜφ funkce (proto, ₧e poΦφtaΦ neumφ spojit data a operace - data jsou v pam∞ti a m∙₧eme napsat funkce, kterß tyto data m∞nφ, ale funkce a data nem∙₧eme p°φliÜ dob°e vßzat). Nemßme tedy ₧ßdnΘ prost°edky pro p°esn∞jÜφ reprezentaci problΘmu.

Objekty a t°φdy

Objektov∞ orientovanΘ programovßnφ nßm umo₧≥uje programov∞ reprezentovat elementy problΘmu. V²sledek tΘto reprezentace je objekt – model n∞jakΘ entity z reßlnΘho sv∞ta. S objekty m∙₧eme provßd∞t r∙znΘ operace, tak jak je tomu i v reßlnΘm sv∞t∞. Objekt tedy obsahuje data, ale i operace, kterΘ je mo₧nΘ s nφm provΘst. Navφc u₧ivatel nemusφ v∞d∞t, jak objekt provßdφ ₧ßdanΘ operace, m∙₧e k n∞mu p°istupovat jako k ΦernΘ sk°φnce.

Ka₧d² objekt je n∞jakΘho typu (tak jako prom∞nnß je n∞jakΘho typu) – v terminologii OOP se °φkß, ₧e objekt je instancφ n∞jakΘ t°φdy. T°φda definuje objekt, nap°. urΦuje, jakΘ operace umφ provßd∞t. Ka₧dß t°φda m∙₧e mφt vφce instancφ (tedy je mo₧nΘ vytvo°it vφce objekt∙ na zßklad∞ jednΘ t°φdy).

Vztahy mezi t°φdami

Program napsan² pomocφ OOP je v₧dy tvo°en n∞jak²mi objekty, kterΘ spolupracujφ, mezi nimi jsou tedy v₧dy n∞jakΘ vztahy. Proto₧e objekty jsou instancemi n∞jak²ch t°φd, vztahy jsou vlastn∞ mezi t°φdami. Pro v∞tÜφ p°ehlednost budu tyto vztahy kreslit, a to za pomocφ diagram∙ jazyka UML (Unified Modeling Language). Pokud tento jazyk neznßte, nevadφ, uvidφte, ₧e diagramy jsou velmi jednoduchΘ. T°φdy se zjednoduÜen∞ kreslφ obdΘlnφkem s nßzvem t°φdy uvnit°, a ka₧d² vztah vysv∞tlφm.

Asociace (association)

Je to vztah, kter² vyjad°uje, ₧e t°φdy "v∞dφ o sob∞" – jsou urΦit²m zp∙sobem propojeny a mohou komunikovat. V diagramu se to znaΦφ Φarou, kterß spojuje t°φdy ·Φastnφcφ se asociace. K tΘto Φß°e p°ipojφme text, vysv∞tlujφcφ asociaci. Nap°φklad vztah zam∞stnance a firmy, pro kterou pracuje, je asociace:

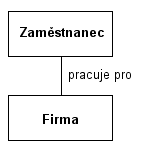
Agregace (aggregation)

Mluvφme o agregaci pokud n∞jakß t°φda obsahuje jinΘ t°φdy (takΘ se jφm °φkß komponenty). Pomocφ agregace m∙₧eme tvo°it slo₧it∞jÜφ t°φdy pomocφ jednoduÜÜφch. Vztah se znaΦφ Üipkou, kterß zaΦφnß u komponenty a konΦφ nevypln∞n²m kosoΦtvercem u t°φdy, kterß komponentu obsahuje. Nap°φklad t°φda Auto obsahuje t°φdu Motor:

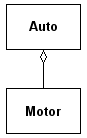
D∞diΦnost

To je pravd∞podobn∞ nejznßm∞jÜφ vztah mezi t°φdami. Pot°ebujeme-li vytvo°it dv∞ t°φdy, kterΘ majφ mnoho spoleΦnΘho (nap°φklad grafick² objekty Φtverec a kru₧nice), byla by Ükoda je vytvo°it odd∞len∞. Mnohem lepÜφ je °φct, ₧e to jsou grafickΘ objekty, tedy "d∞dφ" od t°φdy grafick² objekt (a obsahujφ tedy i operace, kterΘ je mo₧nΘ provΘst s grafick²m objektem), a dßle se liÜφ jen v detailech (obdΘlnφk mß Üφ°ku a dΘlku, kru₧nice mß polom∞r). V podstat∞ mluvφme o d∞diΦnosti pokud jedna t°φda je podmno₧ina druhΘ (druhß t°φda d∞dφ od prvnφ). Prvnφ (od kterΘ se d∞dφ) se naz²vß nadt°φda (takΘ p°edek), a druhß t°φda (kterß d∞dφ) se naz²vß podt°φda (potomek). V diagramu se d∞diΦnost znaΦφ Üipkou od podt°φdy k nadt°φd∞:

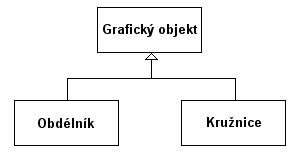
Deklarace a definice t°φd

Po tomto, pro n∞koho pon∞kud nezß₧ivnΘm ·vodu, se m∙₧eme pustit do n∞jakΘho programovßni. Abychom mohli zavΘst do programu n∞jak² nov² objekt, je pot°eba definovat pro tento objekt novou t°φdu. To se provßdφ klφΦov²m slovem class. Zkusφme nap°φklad t°φdu Osoba: 

// deklarace t°φdy
class Osoba {
public:
    char jmeno[30];
    char adresa[50];
};
Deklarovali jsme t°φdu Osoba, kterß obsahuje dv∞ slo₧ky (budeme jim °φkat ΦlenskΘ prom∞nnΘ). Jak vidφte, deklarace se liÜφ od struktury pouze klφΦov²m slovem class, ale p°ibyl nßm °ßdek "public:". ZnaΦφ ·rove≥ p°φstupu k Φlen∙m (od tohoto °ßdku dßle budou mφt vÜechny Φleny ·rove≥ p°φstupu public). Ka₧dß Φlenskß prom∞nnß (a funkce, jak uvidφme pozd∞ji) mß n∞jakou ·rove≥ p°φstupu (member access control), kterß urΦuje, kdo m∙₧e k nφ p°istupovat. Existujφ t°i ·rovn∞ p°φstupu:

┌rove≥
p°φstupu		 Popis
private p°φstup je pouze z t°φdy, ve kterΘ je Φlen deklarovan²
protected p°φstup je pouze z t°φdy, ve kterΘ je Φlen deklarovan², a z t°φd z nφ odvozen²ch d∞diΦnostφ
public p°φstup je z jakΘkoliv t°φdy nebo funkce

Nenφ-li explicitn∞ uvedena ·rove≥ p°φstupu, platφ private.

Pou₧itφ v programu se neliÜφ od pou₧itφ struktury:

Osoba osoba;  // deklare objektu osoba (instance t°φdy Osoba)
strcpy(osoba.jmeno, "Jan Novak");
Ale tφmto p°φkladem jsme si neukßzali skoro nic novΘho, v podstat∞ jsme pouze p°epsali klφΦovΘ slovo struct na class. ╪ekli jsme si v²Üe, ₧e objekt m∙₧e vykonat n∞jakΘ operace. K implementaci operacφ slou₧φ v C++ funkce, kterΘ jsou souΦßstφ t°φdy (jsou v nφ obsa₧enΘ podobn∞ jako ΦlenskΘ prom∞nnΘ jmeno a adresa). Tyto funkce se naz²vajφ ΦlenskΘ funkce nebo takΘ metody. Na rozdφl od obyΦejn²ch funkcφ je mo₧nΘ je zavolat pouze v kontextu n∞jakΘho objektu: 
class Osoba {
public:
    char jmeno[30];
    char adresa[50];
    
    // Φlenskß funkce
    char *vratJmeno() {
        return jmeno;
    }
};
Jak vidφte, nenφ tu ₧ßdn² rozdφl oproti deklaraci obyΦejn²ch funkcφ. Volßnφ se ovÜem provßdφ teΦkovou notacφ, podobn∞ jako se odkazujeme k Φlensk²m prom∞nn²m: 
#include <iostream.h>
#include <string.h>

void main() {
    Osoba osoba;
    strcpy(osoba.jmeno, "Jan Novak");
    
    cout << osoba.vratJmeno() << endl;
}
Proto₧e definice Φlensk²ch funkcφ by mohly b²t dost velkΘ, deklarace t°φdy by se mohla stßt pon∞kud velkou a mΘn∞ p°ehlednou. Proto je mo₧nΘ p°esunout definici Φlensk²ch metod vn∞ deklarace t°φdy: 
class Osoba {
public:
    char jmeno[30];
    char adresa[50];
    
    char *vratJmeno();
};

// definice ΦlenskΘ funkce - pou₧φvß se tzv. cty°teΦkovß notace
char *Osoba::vratJmeno() {
    return jmeno;
}
Jak je vid∞t, definice vypadß jako definice obyΦejnΘ t°φdy, s tφm rozdφlem, ₧e v hlaviΦce je uvedena i t°φda, ke kterΘ tato Φlenskß funkce pat°φ (plnΘ jmΘno tΘto funkce tedy je Osoba::vratJmeno().

Mo₧nß si kladete otßzku proΦ jsme napsali funkci, kterß nßm vracφ n∞jakou Φlenskou prom∞nnou, copak nem∙₧eme k nφ p°istupovat rovnou? V popisu objekt∙ jsme si °ekli, ₧e u₧ivatel k nim m∙₧e p°istupovat jako k ΦernΘ sk°φnce, dostane tedy seznam operaci, ale vφc ne (tomu se °φkß zapouzd°enφ). Kdy₧ mu dßvßme k dispozici p°φmo Φlenskou prom∞nnou, je to poruÜenφ zapouzd°enφ (je pravda, ₧e n∞kdy se v praxi na zapouzd°enφ p°φliÜ nehledφ, ale musφme se sna₧it, aby k takov²m situacφm nedochßzelo). Napsßnφm ΦlenskΘ funkce jeÜt∞ nemßme vyhrßno, u₧ivatel ji m∙₧e, ale nemusφ pou₧φt. Musφme mu tedy zabrßnit v tom, aby se mohl p°φmo odkazovat na Φlenskou prom∞nnou, a to provedeme tak, ₧e ji dßme ·rove≥ p°φstupu private. Proto₧e tφm p°ijdeme o mo₧nost Φlenskou prom∞nnou nastavit, p°idßme metodu nastavJmeno(): 

class Osoba {
private:
    char jmeno[30];
    char adresa[50];
    
public:
    char *vratJmeno();
    void nastavJmeno(char *nove_jmeno);
};

char *Osoba::vratJmeno() {
    return jmeno;
}

void Osoba::nastavJmeno(char *nove_jmeno) {
    strncpy(jmeno, nove_jmeno, 30);
    jmeno[29] = 0;
}

void main() {
    Osoba osoba;
    
    osoba.nastavJmeno("Jan Novak");
    cout << osoba.vratJmeno() << endl;
}
A to je pro dneÜnφ lekci vÜe. P°φÜt∞ budeme pokraΦovat v podobnΘm duchu jako dnes a prohloubφme znalosti o t°φdßch a objekt.

Andrei Badea    

⌐ 2001 Vogel Publishing Vogel Publishing, design by ET NETERA ET NETERA