Maticové počty a některé algoritmy
| Maticové počty patří v Excelu k hůře pochopitelným a tedy málo oblíbeným. Naštěstí pro běžné užití jsou k dispozici již známé postupy a tak uživateli postačí napasovat zveřejněný vzorec do svého sešitu. Příloha k tomuto tématu obsahuje přes 60 příkladů na více jak 200 řádcích. | |
Pojmy
Typ maticové konstanty
Pozn. Práce se skupinou hodnot jako celkem je totožná s myšlenkou "pro každý prvek z celku udělej", jinými slovy, je jakýmsi programátorským cyklem "for each ... in ...". Pokud se autorovi hudby bude zdát skladba přehrávána poněkud vlažně, nepřistoupí k hudebníkům jednotlivě, nýbrž půjde za dirigentem a řekno něco ve smyslu "ať všichni přehrají znovu poslední tři takty a více sforzato". |
|
Každá konstanta má svůj řádkový i sloupcový index a je vlastně prvkem pole. Položky v řádku se oddělují středníkem (;), řádek se ukončuje svislicí (|). Text je uzavřen v uvozovkách, pravdivostní hodnoty nikoliv. Číselné hodnoty se vkládají normálně. {1;2;3|"pondělí";"úterý";"středa"|PRAVDA;NEPRAVDA;PRAVDA}
Příklad je uveden níže v textu. Pozn. Je smutné, že v 80% dostupné literatury (včetně nápovědy pro Excel 2000) se překladatel nenamáhal si svou nápovědu ověřit. Viděl jsem dokonce i text, ve kterém se údajně mají používat jako oddělovače |
|
Podtitulek by mohl znít "a počátky chaosu..". Maticový vzorec je takový vzorec, jehož editace je ukončena stiskem Ctrl+Shift+Enter. Po této akci Excel uzavře váš vzorec do složených závorek. Nesnažte se Excelu pomáhat a tyto vnější závorky dopisovat ručně! Excel by takový zápis bral jako prostý text. Ale! Týká se to pouze vnějších závorek. Pokud ve vzorcích používáte maticou konstantu, pak její hraniční závorky vypsat musíte. Berte to tak, že onen stisk Ctrl+Shift+Enter je vaším tajným signálem pro Excel "posílám matici" a vrácené vnější závorky jako odpověď Excelu "potvrzuji matici". Příklad výpisu z řádků vzorců, kdy maticový vzorec pracuje s maticí A77:A83 {=SUMA(KDYŽ(A77:A83>5;1))-SUMA(KDYŽ(A77:A83>=9;1))}
V maticovém vzorci se nemohou objevit vzorce ani proměnné (například {2^6;3^6;5^6}, {x^6;3^6;5^6}). Výraz {A2;B2;C2} je také neplatný, správný je zápis {A2:C2}. |
| Obsah buňky, která je součástí maticového vzorce, nelze měnit klasickým způsobem (potvrzení klávesou Enter). Použitím Ctrl+Shift+Enter změníte vzorec pro celou oblast, k níž náleží. Pro změnu maticového vzorce tedy nemusíte vybírat celou oblast. Pokud ji přeci jen chcete zvýraznit, použijte při vybrané buňce maticového vzorce zkratkovou klávesu Ctrl+Shift+/ (lomítko na alfanumerické klávesnici) nebo Ctrl+/ (lomítko na numerické části klávesnice). | |
| S buňkou, jež je součástí maticového vzorce, nelze manipulovat (přesun, odstranění, vkládání, ...). Formát buňky je přitom libovolně přizpůsobitelný pro každou buňku matice. Maticové vzorce nelze použít pro sloučené buňky. |
|
"Nepravá" maticová konstanta se nachází na listu a vždy je doprovázena maticovým vzorcem. 
Složené závorky ohraničující "pravou" maticovou konstantu se do vzorce píší ručně, vnější pro maticový vzorec dodá Excel sám. 
Chceme-li vybrat prvek z jednořádkové matice, musíme použít funkci INDEX. Není možné obrátit se k funkci ZVOLIT. To je v souladu s faktem, že matice má vlastnosti pole. 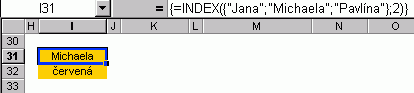
Další příklad ukazuje výhodu maticové konstanty, kdy není zapotřebí samostatné tabulky. 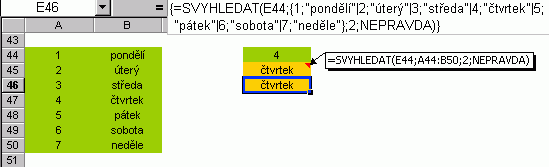
Pamatujete si ještě, že je možné vytvořit nejen pojmenovanou oblast, ale i pojmenovanou konstantu? Stejně tak můžete vytvořit pojmenovanou maticovou konstantu a na tu se poté odkazovat jménem kdekoliv ve vzorcích. Zpřehlední se tak zápis vzorce a sníží se riziko přepsání. 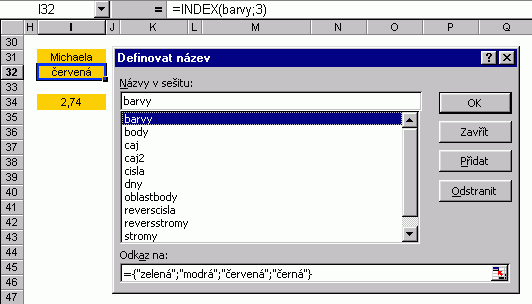
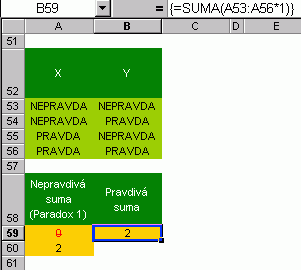
První obrázek z těch následujících ukazuje, že Excel má leckdy problémy s logickými hodnotami. Nejinak je tomu i při použití v maticových vzorcích. Základní chyby a jejich řešení najdete v příloze. Téma "logika" bude ještě zpracováno samostatně. 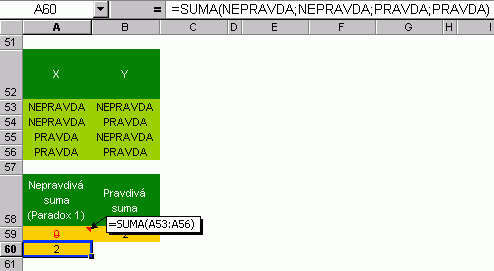
Revers pole hodnot je lahůdkou pro maticové vzorce. Ne tak už pro pochopení principu činnosti. Výsledkem maticového vzorce je v daném případě hodnota. Pro ostatní položky přetáhněte buňku za úchytný bod směrem dolů. 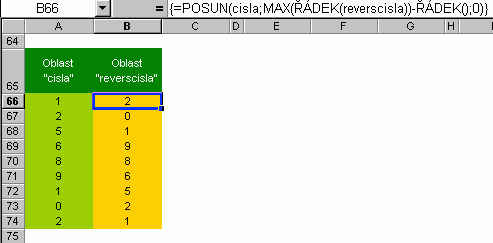
Převracení oblasti patří rovněž do repertoáru maticových vzorců. Vrácena je opět jedna hodnota a vzorec je třeba přetáhnout do dalších buněk. 
Častým požadavkem je suma n-největších či n-nejmenších hodnot z oblasti. 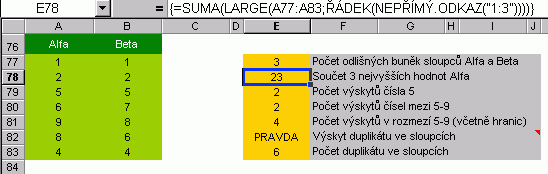
Otázku "Není mezi vámi slečna jménem Adéla?" pokládá následující vzorec. 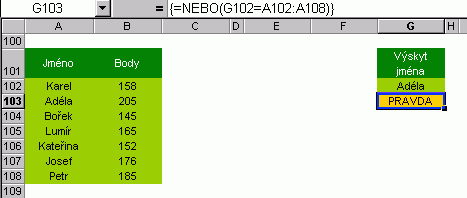
Funkce NEBO ve spojení s maticovým vzorcem může také nahradit několik funkcí IF. 
Mapu vyhodnocení měření lze také udělat s maticovými vzorci. 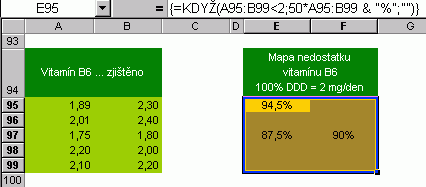
Počet znaků obsažených v řetězci lze spočítat rovněž aplikací maticového vzorce. 
Jak sumarizovat příjmy z každého druhého dne v měsící? Podívejte se na obrázek. 
Zopakovat si můžete i prvočísla.. 
Zjišťování výskytu duplicitních hodnot by si zasloužilo samostanou kapitolu... 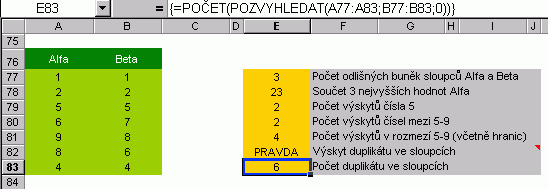
Kumulativní součet už nyní také budete umět zpracovat... Výsledkem je jedna hodnota a vzorec je nutné překopírovat směrem dolů tažením. 
|
Krátce a stručně: Maticové vzorce se uplatní tam, kdy potřebám podmíněného součtu a počtu dochází dech funkcím typu SUMA, POČET a funkcím pro vyhledávání. Uplatňují se dále u překlápění polí a při získávání unikátních položek (toto téma bude samostatně zpracováno časem). |
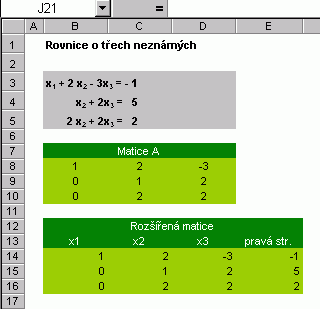
Pokud jste se seznámili s matematikou nad rámec střední školy, pak jste se zcela jistě s pojmem matice setkali. Vy ostatní tento odstavec nepřeskakujte, žádné velké teorie vás nečekají! Budeme se bavit o takové matici (v pravém matematickém slova smyslu), s jejíž pomocí najdeme řešení soustavy tří lineárních rovnic o třech neznámých. Po osvojení si uvedeného postupu budete sami schopni vyřešit jakoukoliv řešitelnou soustavu n-rovnic o n-neznámých. Tři neznámé zde představují x1, x2 a x3. Základní matici A (stále ještě nemluvíme o matici ve smyslu Excelu) sestavíme tak, že číselné konstanty u příslušných proměnných zapíšeme do tabulky. Co řádek matice, to konstanty z jedné rovnice, přičemž za chybějící proměnnou (x1 v druhé a třetí rovnici) si dosadíme 0. Dále zpracujeme tzv. "rozšířenou matici" - ano, pouze vpravo k matici přilepíme sloupec s konstantami pravé části rovnic. Nic na tom není, že? Vrhněme se proto k hledání řešení, kdy už využijeme matice ve smyslu Excelu. Potřebovat budeme jednu skutečnou matici (tzv. "inverzní matici"). Cíle dosáhneme pomocí maticových vzorců. Po prvním použití bude výsledkem matice, ve druhém a dalších hodnota zobrazitelná v jediné buňce (3 řešení). Teorii vztahující se k inverzní matici ponechme stranou. 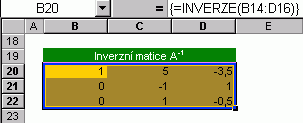
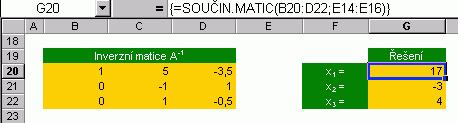 Postup je tentýž i pro jiný počet rovnic a jim odpovídající počet proměnných. Zbývá jen říci oblíbenou větu pedagoga: "Nezapomeňte na zkoušku." Pozn. Nepleťte si funkce SOUČIN.SKALÁRNÍ a SOUČIN.MATIC - viz nápověda. Počty s maticemi mají svá pravidla. Uvádím zde jen to nejpoužívanější, jímž se řídí násobení dvou matic (značení upraveno k obrázku):
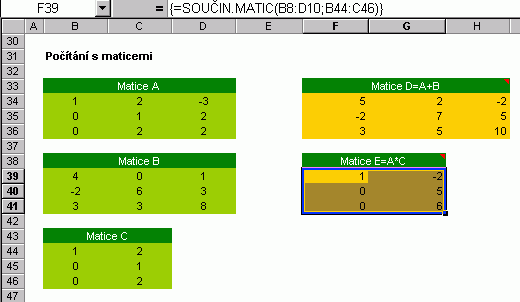 Doporučená literatura: Hans Jochen Bartsch: Matematické vzorce, Mladá fronta, 1996jakákoliv matematická skripta pro první ročník technické vysoké školy |

|