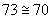
Vyjádření čísla pomocí vyššího řádu nazýváme zaokrouhlování.
· Zaokrouhlování se řídí číslicí na nižším řádu (např. zaokrouhlování na stovky se řídí číslicí na místě desítek).
· Jsou-li na nižším řádu číslice 0, 1, 2, 3, 4, zaokrouhlujeme číslo směrem dolů. Číslice na vyšším řádu nemění svou velikost a číslice na všech nižších řádech nahradíme číslicí 0.
Příklad: Zaokrouhlete a) číslo 73 na desítky
b) číslo 1 449 na tisíce
a) číslo 73 – na místě jednotek je číslice 3 – zaokrouhlujeme směrem dolů
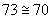
b) číslo 1 449 – na místě stovek je číslice 4 – zaokrouhlujeme směrem dolů
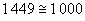
· Jsou-li na nižším řádu číslice 5, 6, 7, 8, 9, zaokrouhlujeme číslo směrem nahoru. Číslici na vyšším řádu zvýšíme o jednu a číslice na všech nižších řádech nahradíme číslicí 0.
Příklad: Zaokrouhlete a) číslo 46 na desítky
b) číslo 871 na stovky
a) číslo 46 – na místě jednotek je číslice 6 – zaokrouhlujeme směrem nahoru
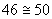
b) číslo 871 – na místě desítek je číslice 7 – zaokrouhlujeme směrem nahoru
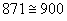
(Materiály převzaty z: MATEMATIKA, Přehled učiva základní školy s řešenými příklady. Fortuna 1999.)
Sbírka úloh z matematiky pro ZŠ (Fr.Běloun a kolektiv) – příklady 32-36.