Funkce může být zadaná různými rovnicemi. Na levé straně je y, na pravé nějaký výraz s proměnnou x.
Například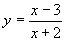 . My ale víme, že se nesmí dělit nulou. Do definičního oboru funkce tedy mohou patřit všechna reálná čísla, vyjma takového x, pro které platí rovnice x + 2 = 0.
. My ale víme, že se nesmí dělit nulou. Do definičního oboru funkce tedy mohou patřit všechna reálná čísla, vyjma takového x, pro které platí rovnice x + 2 = 0.

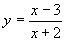 jsou všechna reálná čísla,
jsou všechna reálná čísla, 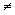 .
.




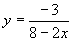 jsou všechna reálná čísla, x
jsou všechna reálná čísla, x  .
.
 ΓÇô2.
–2.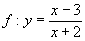 . Doplň tabulku:
. Doplň tabulku: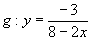 .
.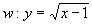 ?
?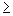
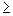 0, jinak by bylo pod odmocninou záporné číslo.
0, jinak by bylo pod odmocninou záporné číslo.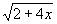 ?
?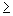 .
. 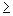 0, jinak by bylo pod odmocninou záporné číslo.
0, jinak by bylo pod odmocninou záporné číslo.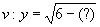 měla jako definiční obor všechna reálná čísla x
měla jako definiční obor všechna reálná čísla x 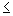 2, musíme na místo otazníku doplnit .
2, musíme na místo otazníku doplnit .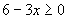 , jinak by bylo pod odmocninou záporné číslo.
, jinak by bylo pod odmocninou záporné číslo.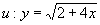 doplň tabulku:
doplň tabulku: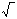
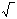
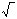
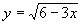 .
.
