 | Je třeba to přečíst, ! Ale to nebolí. |
Zaznamenání všech bodů, jejichž souřadnice vyhovují přiřazení (kterému říkáme funkce), znamená sestrojení grafu této funkce.
 | Je třeba to přečíst, ! Ale to nebolí. |
| 10. od konce |
Funkce je zadána opět tabulkou:
| X | –2,5 | –1 | 0 | 0,5 | 2 | 3 | 5 |
| Y | –1,5 | –2,4 | –1 | 5 | 0 | 1,5 | 3 |
Vyberte z následujících obrázků A, B, C, D graf této funkce.
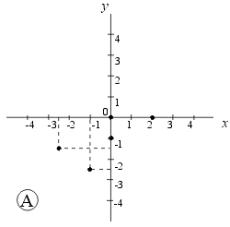
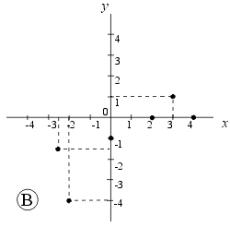
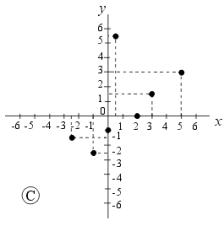
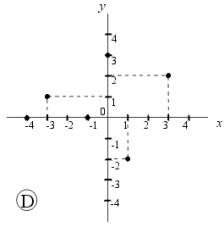
Grafem je .

 | Doplň, co tam patří! |

|
Myslíš to vážně? Tak si to ještě rozvaž!
|
 |
Vidím, že na tebe si jen tak nepřijdu… |
 |
Netruchli , všechno zlé je k něčemu dobré. A tohle ještě nebylo až tak zlé. |
| 9. od konce |
Funkce je dána tímto grafem:
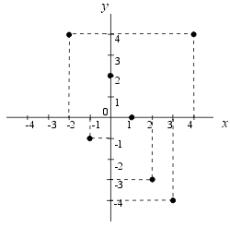
Vyplňte tuto tabulku souřadnicemi bodů, které tvoří graf funkce (body seřaďte podle x-ové hodnoty):
| x | |||||||
| y |

 | Doplň, co tam patří! |

|
, správně jsi z 14.
Budu shovívavá a dám ti ještě další šanci…
|

|
, správně jsi z 14.
Já vím, že to umíš, tak se soustřeď a těch pár omýlků neomylně smyj!
Buď ! |
 |
, děláš mi radost, není tam nic, co by nebylo dobře! |
 |
, správně jsi z 14.
Teď už ty chyby nevygumuješ, tak příště.
|
| 8. od konce |
Do definičního oboru předcházející funkce patří čísla:
 | Která odpověď je správná? |

|
Hm, tak to právě není. Zkus to jinak.
Do definičního oboru patří jen x–ové souřadnice bodů, které jsou zaznamenány v grafu. |
 |
To je ončo, milá Tončo! |
 |
Dobře to není, ale stejně ses to , nebo ne? |
| 7. od konce |
Do oboru funkčních hodnot předcházející funkce patří čísla:
 | Která odpověď je, , správná? |

|
Ať koukám, jak koukám, správnou odpověď nevidím. Máš ještě další pokus.
Do definičního oboru patří jen y–ové souřadnice bodů, které jsou zaznamenány v grafu. |
 |
To je přesně to, co jsem chtěla vidět...! |
 |
Chybama se člověk učí...učíš se taky? |
Funkce může být zadána, jak jsme viděli, tabulkou, grafem a také rovnicí (vzorcem).
 | Přečti si text! |
| 6. od konce |
Zvolíme jako příklad zadání funkce rovnicí ten nejjednodušší příklad: Rovnici y = x. V tom případě část tabulky vypadá takto:
| X | –2 | –1 | 0 | 1 | 2 | 3 | 4 |
| Y |

 | Vepiš správné odpovědi! |

|
, správně jsi z 7.
Určitě nebude problém se zamyslet a těch pár přehmatů vyhmátnout!
Pracuj pozorněji. |
 |
Lépe už to ani nešlo! |
 |
, správně jsi z 7.
Ty chyby zamrzí, ale příště jim nedáme šanci.
|
| 5. od konce |
Tabulka může libovolně dlouho pokračovat, neboť reálných čísel je nekonečně mnoho a my jejich počet nemáme ničím omezený. Rovnice y=x nezakazuje žádné reálné číslo použít. Tak doplň tabulku:
| X | –1,9 | 0,3 | ||||
| Y | –2,5 | 1,9 | 2,9 | 45 |

 | Doplň správné odpovědi! |

|
, správně jsi z 6.
Ještě to zkus opravit, ať ti mohu zatleskat!
To ses asi jen . |
 |
Přímo pohádkový výkon! |
 |
, správně jsi z 6.
Co ten zbytek?
|
| 4. od konce |
Protože rovnice y = x nezakazuje žádné reálné číslo použít, jsou definičním oborem této funkce všechna čísla.

 | Dokážeš to správně vyplnit, ? |

|
Bohužel, není to dobře, zkus to ještě jednou.
Jaké znáš číselné obory? |
 |
Bingo! |
 |
Nic si z toho nedělej, , já taky občas udělám chybu. |
| 3. od konce |
Když zadáme jinou rovnici, třeba y = 2x + 3, dosazujeme za x různá čísla a vypočítáváme y. Dostáváme tak body [x, y], které tvoří graf této funkce. Na grafu této funkce leží body:
 | Vyber správné odpovědi! |

|
, správně jsi z 7.
Udělej tetě Elvíře radost a ty chyby vyhoď z okna! (Pozor na lidi na chodníku…)
první řádek : 3 = 2 . 0 + 3 |

|
, správně jsi z 7.
Chybí jenom málo k tomu, abych žasla nad tvou neomylností. Co s tím uděláš?
čtvrtý řádek: 7 = 2 . 2 + 3 |
 |
Jede ti to skvěle! |
 |
, správně jsi z 7.
To nic, nikdo nejsme dokonalý.
|
Vždy je lepší pracovat s objekty, které mají jméno nebo označení. Funkce se označují malými písmeny, např.: f, g, h, w atd. Předchozí funkci pojmenujeme třeba f.
Zapíše se to takto: f: y = 2x + 3.
Přečte takto: Funkce f je dána rovnicí y = 2x + 3.
 | Přečti si to pozorně! |
| 2. od konce |
Máme funkci g: y = x2 – 1
Na grafu této funkce leží body:
 | Které z odpovědí jsou správné? |

|
, správně jsi z 6.
Máš na to ty drobnosti vychytat a mít to na 100%!
třetí řádek: |
 |
Zase bez chyby? Určitě se teprve hlásíš na střední školu? Neučíš tam náhodou? |
 |
, správně jsi z 6.
Ještě máš co vylepšovat.
|
| 1. od konce |
V následujících obrázcích A, B, C, D, E jsou v soustavách souřadnic vyznačeny „nějaké čáry“.
Který z obrázků představuje graf funkce?
 | Rozhodni, kde ano a kde ne! |

|
, správně jsi z 5.
A co ten zbytek? Zkusíš ho také pokořit?
Žádné body „čáry“ nesmí být „pod sebou“. |
 |
, víš, co je nového? Máš to bez chyby! |
 |
, správně jsi z 5.
I když nemáš všechno dobře, stejně se pořád učíš.
|

