 | Přečti si to pozorně! |
Nejdříve si zopakujeme nezbytné základy . Nepochybuji o tom, že umíš zakreslit body do soustavy souřadnic, ale radši si to prověříme. Řekneme si, jak poznáme funkci, jaké jsou její vlastnosti a hlavně jak funkci nakreslíme její graf. V této lekci Tě nečeká závěrečný testík. Ten prověří tvoje znalosti až na konci další lekce „Funkce - přímá úměrnost.“
 | Přečti si to pozorně! |
| 9. od konce |
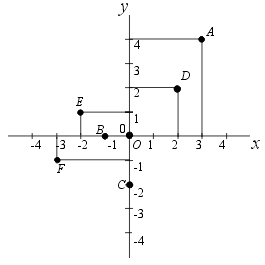
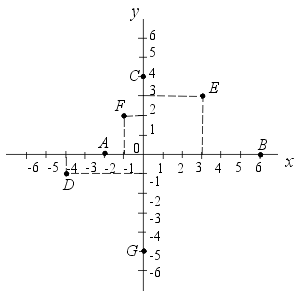
Body v soustavě souřadnic jsou označeny písmeny O, A, B, C, D, E, F. Napiš jejich souřadnice:
O = [, ],
A = [, ],
B = [, ],
C = [, ],
D = [, ],
E = [, ],
F = [, ]

 | Vepiš správné odpovědi! |

|
, správně jsi z 14.
Já vím, že to umíš, tak se soustřeď a těch pár omýlků neomylně smyj!
A = [?, 4] |

|
, správně jsi z 14.
Určitě nebude problém se zamyslet a těch pár přehmatů vyhmátnout!
O = [0, 0], A = [3, 4], B = [–1, 0], C = [0, –2], D = [2, 2], E = [–2, 1], F = [–3, –1] Podívej se na pojem funkce . |
 |
Připadá mi to až podezřelé, ale není tam ani jeden přehmat! |
 |
, správně jsi z 14.
To je mrzuté. Už jsem měla připravenou báječnou pochvalu…
|
| 8. od konce |
Jen pro zopakování: bod O se jmenuje soustavy souřadnic.

 | Doplň, co tam patří! |

|
ses? Pořádně si to ještě pročti.
Jeho název začíná: p… |
 |
Samozřejmě je to dobře. |
 |
Nevěš hlavu, , i mistr tesař se někdy utne. |
| 7. od konce |
Svislá osa se nazývá –ová, vodorovná –ová.

 | Doplň správné odpovědi! |

|
, správně jsi z 2.
Ještě to zkus opravit, ať ti mohu zatleskat!
Svislá je y–ová (ypsilonová). |

|
, správně jsi z 2.
Udělej tetě Elvíře radost a ty chyby vyhoď z okna! (Pozor na lidi na chodníku…)
Vodorovná je x–ová (iksová). |
 |
Nemám slov! Perfektní! |
 |
, správně jsi z 2.
Co jsi ?
|
| 6. od konce |
Jestliže bod A = [x, y], říkáme, že x je souřadnicí bodu A a y je druhou souřadnicí bodu A.

 | Dokážeš to správně vyplnit, ? |

|
Vedle jak ta jedle. Víš proč?
Když je y druhou souřadnicí, tak x je… |
 |
Zásah! |
 |
Je tam chyba, ale my přece zatím jenom trénujeme, že? |
| 5. od konce |
Teď naopak. Máš body a znáš jejich souřadnice:
P = [6, 0], R = [0, 4], S = [–2, 0], T = [0, –5], U = [3, 3], V = [–1, 2], Z = [–4, –1]. Přiřaď tyto body k bodům na obrázku, které jsou značeny A, B, C, D, E, F, G.
P 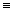 , R
, R 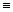 , S
, S 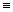 , T
, T  , U
, U  , V
, V  , Z
, Z 

 | Doplň, co tam patří! |

|
, správně jsi z 7.
Chybí jenom málo k tomu, abych žasla nad tvou neomylností. Co s tím uděláš?
Nepiš malá písmena. |
 |
Chválím tě, chválím tě, chválím tě (doufám, že ti to nestoupne do hlavy). |
 |
, správně jsi z 7.
K naprosté dokonalosti ti ještě krůček schází.
|
| 4. od konce |
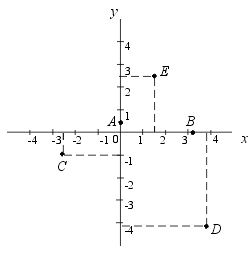
Body mají souřadnice značené [x, y]. x, y nemusí být samozřejmě celá čísla. Zadáme si několik bodů tabulkou:
|
| P | R | S | T | U |
| X | 1,5 | –2,4 | 0 | 3,9 | 3,2 |
| Y | 2,5 | –1 | 0,5 | –4,2 | 0 |
Např. bod P = [1,5;2,5] má x-ovou souřadnici 1,5 a y-ovou 2,5.
Přiřaď opět tyto body k bodům na obrázku, které jsou značeny A, B, C, D, E.
P , R
, R  , S
, S  , T
, T  , U
, U 

 | Vepiš správné odpovědi! |

|
, správně jsi z 5.
Máš na to ty drobnosti vychytat a mít to na 100%!
Více se soustřeď. |
 |
Ó, , klaním se až k zemi! |
 |
, správně jsi z 5.
Nešlo to bez chyb? Ale stejně ses to , viď?
|
V tabulce jsou x–ovým hodnotám přiřazovány hodnoty y–ové. Takovému přiřazení se říká funkce. Musí však být splněna jedna důležitá podmínka:
Jedné x–ové hodnotě nesmí být přiřazeny dvě různé y–ové hodnoty.
 | Přečti si to! |
| 3. od konce |
Kdybychom znovu přiřazovali x–ovým hodnotám hodnoty y–ové, pak by následující tabulka funkci nepředstavovala:
| X | 1,5 | –2,4 | 0 | 1,5 | 3,2 |
| Y | 2,5 | –1 | 0,5 | –4,2 | 0 |
Proč? Protože v prvním a čtvrtém sloupci jsou stejným x–ovým hodnotám přiřazeny
y–ové .
inspiruj se textíkem

 | Doplň správné odpovědi! |

|
, správně jsi z 2.
A co ten zbytek? Zkusíš ho také pokořit?
Viz podtržená věta před tímto příkladem. |
 |
Máš to všechno a máš to správně. Co dodat? |
 |
, správně jsi z 2.
Škoda těch pár přehmatů.
|
| 2. od konce |
Kdybychom znovu přiřazovali x–ovým hodnotám hodnoty y–ové, pak by následující tabulka:
| x | 2,5 | –1 | 0,5 | –4,2 | 0 |
| y | 1,5 | –2,4 | 0 | 1,5 | 3,2 |
 | Která z nabízených odpovědí je správná? |

|
Pročti si to ještě jednou, něco tam nehraje.
Toto zadání není v rozporu s podtrženou větou, která je napsaná před 7. příkladem. |
 |
Správná volba! |
 |
Ještě není všem dnům konec, my ty chyby pokoříme, to mi věř! |
Souhrnu všech čísel (množině čísel), kterým přiřazujeme y–ové hodnoty, se říká definiční obor. Ten se značí písmenem D. Souhrnu všech čísel y se říká obor hodnot. Ten se značí písmenem H.
Věta „jedné x–ové hodnotě nesmí být přiřazeny dvě různé y–ové hodnoty“ tedy tvrdí, že každému x 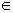 D se může přiřadit nejvýše jedno y
D se může přiřadit nejvýše jedno y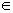 H, má–li být přiřazení funkcí. To u 7. příkladu splněno není. Naopak nic nebrání tomu, aby různým x
H, má–li být přiřazení funkcí. To u 7. příkladu splněno není. Naopak nic nebrání tomu, aby různým x 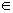 D byla přiřazena stejná y. Tak tomu je u 8. příkladu.
D byla přiřazena stejná y. Tak tomu je u 8. příkladu.
 | Je třeba to přečíst, ! Ale to nebolí. |
| 1. od konce |
V následujících obrázcích A, B, C, D, E jsou v soustavách souřadnic vyznačeny body. Které z obrázků představují funkce?
 | Rozhodni, kde ano a kde ne! |

|
, správně jsi z 5.
Dám ti ještě šanci mít to úplně bez chyb.
Body nesmí být „pod sebou“. |
 |
Lépe už to ani nešlo! |
 |
, správně jsi z 5.
Nešlo to bez chyb?
|

