Prehľad základných vzťahov z fyziky I
1. Rýchlosť
![]()
r – polohový vektor bodu v priestore vzhľadom na začiatočný bod pravouhlej súradnicovej sústavy
Rýchlosť je vektor, ktorý je rovnobežný s dotyčnicou k pohybovej čiare v príslušnom bode a je orientovaný na stranu pohybu. Podiel Ds/Dt sa volá stredná rýchlosť v0.
2. Zrýchlenie
![]()
v – rýchlosť, r – polohový vektor vzhľadom na začiatok súr. sústavy
Zrýchlenie je prvá derivácia rýchlosti alebo druhá der. polohového vektora podľa času. Je daná čiara k so začiatkom O. Pohyb ľubovoľného bodu A na čiare k určuje jeho vzdialenosť u od bodu O. Pohyb bodu určuje jediná skalárna funkcia času u = f(t).
3. Uhlová rýchlosť
![]()
Pohybujúci sa bod vytvára v priestore svoju trajektóriu, jeho sprievodič kužeľovú plochu. Nech j je uhol, ktorý vytvorí sprievodič na tejto ploche za čas t. Derivácia w = dj /dt sa nazýva uhlová rýchlosť.
4. Uhlové zrýchlenie
![]()
Vektor w s tou istou absolútnou hodnotou, ktorý je na rovinu určenú polohovým vektorom r a vektorom v kolmý a orientovaný tak, že sústava vektorov v, r a je pravotočivá sa nazýva vektor uhlovej rýchlosti stáčania sprievodiča. Jeho derivácia podľa času sa nazýva vektor uhlového zrýchlenia.
5. Tangenciálne zrýchlenie
![]()
v – rýchlosť, t - jednotkový vektor rovnobežný s dotyčnicou a orientovaný na stranu pohybu (v = vt)
6. Normálové zrýchlenie
![]()
![]()
v – absolútna hodnota rýchlosti, v – rýchlosť, k* = dt / ds, r – jednotkový vektor v smere polomeru krivosti kružnice, ktorý končí v bode dotyku kružnice krivosti s danou priestorovou čiarou
7. Súvis obvodovej a uhlovej rýchlosti
![]()
v – obvodová rýchlosť, w - uhlová rýchlosť, r – polohový vektor bodu vzhľadom na zvolené miesto
8. Zákon zotrvačnosti
Existuje aspoň jedna súradnicová sústava vzhľadom ku ktorej teleso zostáva v pokoji alebo v rovnomernom priamočiarom pohybe dokiaľ naň nepôsobia silami iné telesá. Takúto vzťažnú sústavu nazývame inerciálnou sústavou.
9. Zákon sily
![]() [F] = N
[F] = N
Sila pôsobiaca na HB je úmerná súčinu jeho hmotnosti a zrýchlenia.
10. Zákon akcie a reakcie
Pôsobenie telies je vždy vzájomné. Ak prvé teleso pôsobí na druhé nejakou silou F12 pôsobí súčasne druhé teleso na prvé silou F21 pričom F12 = - F21. Obe sily ležia na tej istej vektorovej priamke, súčasne vznikajú a zanikajú.
11. Hybnosť
![]()
m – hmotnosť, v – rýchlosť
12. Impulz sily
- je jej časovým účinkom
ak: F = konst. Þ ![]()
F
¹ konst. Þ 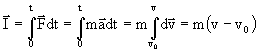 alebo:
alebo: ![]()
Impulz sily pôsobiaci na HB sa rovná zväčšeniu jeho hybnosti, H0 – počiatočná, H – konečná hybnosť
13. Práca sily
- dráhový účinok sily
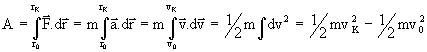 [J]
= [N.m] = [kg.m2.s-2]
[J]
= [N.m] = [kg.m2.s-2]
½mv2 – ½mv02 – ak na HB s hmotnosťou m pôsobí sila F, udeľuje mu táto sila zrýchlenie dané vzťahom F = ma a koná pritom prácu
r – sprievodič (pol. vektor) pôsobiska sily, r0, rK – pol. vektor počiatočného a konečného bodu dráhy, po ktorej sila pôsobí
14. Kinetická energia
- pohybujúci sa HB má schopnosť konať prácu – má energiu. Energia pohybujúceho sa bodu má svoju príčinu v jeho pohybe.
![]()
Veta o kinetickej energii: práca, ktorú sila na HB pôsobiaca vykonala na určitej dráhe sa rovná zvýšeniu kinetickej energie HB:
A = ½ mv2 – ½ mv02
15. Potenciálna energia v homogénnom gravitačnom poli
- PE HB s hmotnosťou m v určitom mieste gravitačného poľa, vzhľadom na nejaký vzťažný bod je daná prácou, ktorú vykonávajú sily poľa pri prechode tohto HB z miesta, v ktorom sa na Ep pýtame, na miesto vzťažné.
- v homogénnom (zemskom) gravitačnom poli:
![]()
h – vzdialenosť telesa od Zeme
- v gravitačnom poli jedného HB s hmotnosťou M:
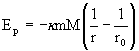
r – vzdialenosť miesta, v ktorom hľadáme PE bodu m od bodu M, vzdialenosť vzťažného bodu od bodu M
16. Výkon sily
![]()
Výkon sily je hraničná hodnota podielu vykonanej práce DA za čas D t
17. Moment sily
Moment sily pôsobiacej v bode A, vzhľadom na bod O je vektorový súčin polohového vektora r a pôsobiska sily F vzhľadom na bod O
![]()
18. Moment hybnosti
Moment hybnosti popisuje pohybový stav rotujúceho telesa
![]()
r – polohový vektor HB vzhľadom na bod O, m – hmotnosť, v – rýchlosť
19. Sila zotrvačnosti
![]()
m - hmotnosť, a0 – spomalenie
![]() v neinerciálnej
sústave
v neinerciálnej
sústave ![]()
20. Hmotný stred sústavy hmotných bodov (SHB)
Bod T na spojnici dvoch HB, ktorý túto spojnicu delí v obrátenom pomere ich hmôt sa nazýva ťažisko (hmotný stred) týchto bodov
![]()

21. Prvá veta impulzová pre SHB
![]()
alebo: ![]()
Súčet všetkých vonkajších síl pôsobiacich na jednotlivé body sústavy sa rovná derivácii celkovej hybnosti podľa času
22. Druhá veta impulzová pre SHB
![]()
D – značí súčet všetkých na sústavu pôsobiacich momentov vonkajších síl, G – moment hybnosti (G = ri ´ mivi)
Súčet momentov vonkajších síl pôsobiacich na jednotlivé HB sústavy sa rovná derivácii celkového momentu hybnosti sústavy podľa času
23. Veta o pohybe hmotného stredu SHB
Za účinku vonkajších síl ťažisko (hmotný stred) sa pohybuje tak, ako keby celá hmota bola sústredená v ťažisku a všetky sily účinkovali v ťažisku.
24. Tuhé teleso
Jeho tvar a objem nemožno meniť nijakými silami. Jeho ktorákoľvek dvojica bodov zachováva počas pohybu telesa svoju vzájomnú vzdialenosť.
25. Moment zotrvačnosti SHB
![]()
ai – je kolmá vzdialenosť HB mi od osi na ktorú sa J vzťahuje
26. Moment zotrvačnosti tuhého telesa
Pri telese spojite vyplneného hmotou:
![]()
27. Steinerova veta
Moment zotrvačnosti J vzhľadom na ľubovoľnú priamku sa rovná jeho momentu zotrvačnosti J* vzhľadom na priamku idúcu ťažiskom telesa a s danou ľubovoľnou priamkou rovnobežnú, zväčšenému o príspevok ťažiska s celou hmotnosťou v ňom sústredenou
![]()
M – celková hmotnosť telesa, a – vzdialenosť ťažiska od osi
Moment zotrvačnosti vzhľadom na ľubovoľnú priamku:
![]()
T – tenzor hybnosti v ľubovoľnom bode priamky, T* – tenzor hybnosti v ťažisku, r – jednotkový vektor v smere priamky vzhľadom na ktorú hľadáme moment zotrvačnosti
28. Kinetická energia rotačného pohybu tuhého telesa
Teleso sa otáča uhlovou rýchlosťou w. Pretože kinetická energia telesa sa rovná súčtu energií jeho hmotných elementov, kinetická energia okolo nehybnej osi je:
![]()
![]()
J – moment zotrvačnosti vzhľadom na os otáčania, w – uhlová rýchlosť
Pozn.: Kinetická energia úplne voľne sa pohybujúceho sa telesa je EK = ½ Mv*2 + ½ J*w2
M – hmotnosť telesa, v* – rýchlosť ťažiska telesa, J* – moment zotrvačnosti telesa vzhľadom na jeho okamžitú os otáčania, prechádzajúcou jej ťažiskom, w – uhlová rýchlosť otáčania
29. Pohybové rovnice tuhého telesa
![]()
F – sila, m – hmotnosť, a – zrýchlenie
rotačný pohyb:
![]()
D – súčet všetkých momentov vonkajších síl vzhľadom na os otáčania, J – moment zotrvačnosti vzhľadom na os otáčania, e – uhlové zrýchlenie
30. Podmienky rovnováhy tuhého telesa
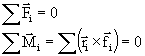
Súčet vonkajších síl pôsobiacich na teleso sa musí rovnať nule, súčet momentov sa musí rovnať nule.
31. Moment hybnosti rotujúceho telesa
![]()
ri – pol. vektor vzhľadom na bod O
![]()
![]()
G – moment hybnosti, v0 – rýchlosť ľubovoľne zvoleného bodu telesa, vi – rýchlosť ktoréhokoľvek bodu tohto telesa
vi = v0 + w´r·, m – hmotnosť, w – uhlová rýchlosť, J – moment zotrvačnosti tuhého telesa.
32. Izolovaná sústava HB
Sústava telies, sa nazýva izolovaná, ak žiadna jej časť nie je v interakcii so žiadnym hmotným objektom nepatriacim sústave, teda na izolovanú sústavu nepôsobia vonkajšie sily. Ak telesá tvoriace sústavu, môžeme nahradiť HB-mi, hovoríme o sústave HB-ov.
33. Zákony zachovania pre izolovanú SHB
1. zákon o zachovaní hybnosti:
Celková hybnosť izolovanej sústavy je konštantná:
![]()
2. zákon o zachovaní momentu hybnosti:
Celkový moment hybnosti izolovanej sústavy je konštantný:
![]()
34. Sila šmykového trenia
Statické trenie
![]()
FN – kolmá sila, ktorá teleso pritláča (normálna sila), mS – súčiniteľ šmykového trenia
Dynamické trenie
![]()
mD – súčiniteľ šmykového trenia
mS > mD
35. Newtonov gravitačný zákon
Sila, ktorou pôsobí teleso s hmotnosťou m1 na teleso s hmotnosťou m2
![]()
r = ½r12½, r12 – polohový vektor telesa m2 vzhľadom na teleso m1, k – Newtonova gravitačná konštanta
36. Intenzita gravitačného poľa
Intenzita HB s hmotnosťou M, kde r je polohový vektor bodu, v ktorom intenzitu hľadáme vzhľadom na HB s hmotnosťou M.
½r½ = r
![]()
m – hmotnosť HB, F – gravitačná sila, k – Newtonova gravitačná konštanta
37. Potenciálna energia v gravitačnom poli vzhľadom na nekonečno
![]()
r – vzdialenosť miesta, v ktorom hľadáme pot. energiu HB s hmotnosťou m vzhľadom na HB s hmotnosťou M, k je Newtonova gravitačná konštanta
38. Potenciál gravitačného poľa
![]()
EP – potenciálna energia HB hmotnosti m v danom mieste
vzhľadom na nekonečno: v okolí jedného HB s hmotnosťou M, r je vzdialenosť miesta, v ktorom hľadáme potenciál vzhľadom na HB s hmotnosťou M.
![]()
39. Vzťah medzi intenzitou a potenciálom gravitačného poľa
![]()
K – intenzita gravitačného poľa, V – potenciál gravitačného poľa
kde:
![]()
![]()
40. Pohybová rovnica pre netlmený harmonický oscilátor (HO)
(F = -kx)
![]()
Pohybová rovnica HB s hmotnosťou m, kde x je výchylka HB z rovnovážnej polohy, k je konštanta charakterizujúca vlastnosti zariadenia, ktoré núti konať HB harmonický pohyb
41. Uhlová frekvencia netlmeného HO
![]()
k – konštanta charakterizujúca vlastnosti zariadenia, ktoré núti HB konať harmonický pohyb, m – hmotnosť HB
42. Závislosť výchylky HO od času
![]()
w – uhlová frekvencia, x0 – amplitúda, a – fázová konštanta, t – čas, (wt + a) – fáza pohybu
43. Pohybová rovnica tlmeného HO
![]()
r – koeficient odporu prostredia, k – konštanta charakterizujúca vlastnosti zariadenia, ktoré núti konať HB harmonický pohyb, m – hmotnosť, x – výchylka HB z rovnovážnej polohy
44. Útlm HO
Podiel dvoch po sebe idúcich maximálnych výchyliek na tú istú stranu
![]()
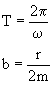 , T – perióda harmonického tlmeného pohybu, w – uhlová
frekvencia, b – koeficient útlmu, r – koeficient odporu prostredia, m – hmotnosť
, T – perióda harmonického tlmeného pohybu, w – uhlová
frekvencia, b – koeficient útlmu, r – koeficient odporu prostredia, m – hmotnosť
45. Rezonančná frekvencia HO
(Vynútené kmity)
Harmonicky sa meniaca vonkajšia sila f = f0sin w2t
Pohybová rovnica:
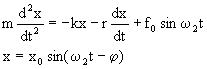
x0, j = konšt.
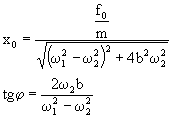
REZONANCIA – keď w2 je také, že x0 má max výchylku
![]()
w1 – uhlová frekvencia, b – koeficient útlmu
46. Hookov zákon pre deformáciu v ťahu
![]()
σ – normálové napätie, E – modul pružnosti v ťahu, ε – relatívne predĺženie
![]()
Δl = l – l0
l0 – pôvodná dĺžka, l – konečná dĺžka
47. Hookov zákon pre deformáciu v šmyku
![]()
τ – tangenciálne napätie, γ – relatívne posunutie hornej základne vzhľadom na dolnú, G – modul pružnosti v šmyku
48. Hydrostatický tlak
![]()
FG – tiažová sila kvapaliny, S – plocha
FG = mg = Shgρ
h – hĺbka od povrchu kvapaliny, ρ – hustota kvapaliny, g – tiažové zrýchlenie
49. Archimedov zákon
Na teleso ponorené do tekutiny (kvapalina, plyn) pôsobí tekutina vztlakom, ktorý sa rovná tiaži takého množstva kvapaliny, ktoré zaujíma rovnaký objem ako ponorená časť telesa.
![]()
50. Rovnica kontinuity
v1S1 = v2S2
S1,2 – prierezy trubice, v1,2 – rýchlosti prúdenia kvapaliny
51. Bernoulliho rovnica
![]()
Pri ustálenom nevírivom prúdení ideálnej kvapaliny je súčet kinetickej a potenciálnej energie objemovej jednotky kvapaliny a tlaku všade rovnaký
![]()
ρ – hustota (merná hmotnosť), v – rýchlosť, p – tlak, h – výška, g – gravitačné zrýchlenie
52. Stavová rovnica pre ideálny plyn
Pre tlak plynu platí vzorec:
![]()
N – počet molekúl, V – objem plynu, m0 – hmotnosť molekuly, vk – stredná kvadratická rýchlosť, EK – kinetická energia posuvu molekúl
Stavová rovnica:
![]()
k – Botzmanova konštanta, T – termodynamická teplota, p – tlak, V – objem, N – počet molekúl,
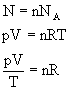
n – látkové množstvo, R = NA n – mólová plynová konštanta
53. Rovnica pre adiabatický dej
dA + dU = 0
dA = p dV, dU = CV dT
dQ = 0
dQ = CV dT + p dV
CV dT + p dV = 0
dA = – dU
Q – teplo, A – práca plynu, U – vnútorná energia, CV – tepelná kapacita za stáleho objemu, T – teplota, p – tlak, V – objem
54. Adiabatický dej
Adiabatický dej prebieha pri dokonalej tepelnej izolácii sústavy. Pri adiabatickom deji plyn teda teplo od svojho okolia ani neprijíma, ani ho nevydáva, teda dQ = 0.
Energiu získava prostredníctvom práce. Analogicky okoliu plyn odovzdáva energiu len prostredníctvom práce: dA’ = – dU
55. Poissonova konštanta
![]()
CP – tepelná kapacita za stáleho tlaku, CV - tepelná kapacita za stáleho objemu
56. Mayerova rovnica
CP = CV + R
CV – tepelná kapacita za stáleho objemu, CP – tepelná kapacita za stáleho tlaku, R – plynová konštanta
57. Kilomolové teplo za stáleho tlaku
![]()
(dQ)p = CPdT
CP – tepelná kapacita za stáleho tlaku, Q – teplo, T – teplota, p – tlak
58. Kilomolové teplo za stáleho objemu
![]()
CV – tepelná kapacita za stáleho objemu, Q – teplo, T – teplota, V – objem
59. Práca plynu
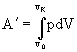
p – tlak plynu, v0 – počiatočný, vK – konečný objem plynu, V – objem
60. Prvá veta termodynamická
Zmena vnútornej energia dU sústavy sa rovná súčtu práce dÁ vykonanej okolím a tepla dQ prijatého od okolia, teda:
dU = dÁ + dQ
61. Vnútorná energia plynu
dU = CV dT
T – Kelvinova teplota, CV – tepelná kapacita za stáleho objemu
62. Teplo
Veličina určená energiou, ktorú pri tepelnej výmene odovzdá jedna sústava druhej.
Q = C dT
C – tepelná kapacita, T – teplota
Q = m c dT
c – merná tepelná kapacita, m – hmotnosť
63. Ekvipartičný teorém
![]()
i – počet stupňov voľnosti molekuly, k – Boltzmanova konštanta, T – termodynamická teplota
64. Entropia
Keď pri elementárnej zmene svojho stavu sústava látok pri teplote T vratným spôsobom naberie množstvo tepla dQ, zmení sa jej entropia o hodnotu dS
![]()
dQ – elementárne tepelné množstvo, ktoré bolo sústavou látok pri teplote T vratným spôsobom prijaté
65. Účinnosť ideálneho tepelného stroja
![]()
T1 – teplota ohrievača, T2 – teplota chladiča
66. Druhá veta termodynamická
a) nemožno zostrojiť trvalo pracujúci tepelný stroj, ktorý by nič iného nespôsoboval, len odoberal teplo zo zásobníka a konal rovnocennú prácu (mechanickú)
b) pri styku dvoch telies s rozličnou teplotou teplo prechádza vždy len s teplejšieho telesa na studenšie
67. Coulombov zákon (slovne aj vzorcom)
Dva bodové elektrické náboje v pokoji pôsobia na seba silou, ktorá je priamo úmerná súčinu ich veľkostí a nepriamo úmerná druhej mocnine ich vzdialenosti
![]()
F12 – sila ktorou účinkuje náboj q1 na el. náboj q2, r12 – polohový vektor el. náboja q2 vzhľadom na el. náboj q1, k0 – konštanta úmernosti
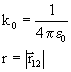 , ε0
– permitivita vákua
, ε0
– permitivita vákua
68. Intenzita elektrického poľa (definícia)
- je podiel sily F, ktorá účinkuje na el. náboj q v elektrickom poli, teda:
![]()
69. Potenciálna energia elektrostatického poľa vzhľadom na nekonečno (definícia)
Potenciálna energia náboja Q’, vzhľadom na nekonečno v elektrostatickom poli bodového náboja Q je daná vzťahom:
![]()
r – vzdialenosť náboja Q’ od náboja Q
70. Potenciál elektrostatického poľa (definícia)
Potenciál elektrostatického poľa v určitom mieste poľa je definovaný ako podiel potenciálnej energie náboja Q’ v uvažovanom mieste tohto náboja, t. j.
![]()
71. Potenciál elektrostatického poľa vzhľadom na nekonečno (definícia)
Ak ide o elektrostatické pole bodového náboja Q, potenciál vzhľadom na nekonečno je:
![]()
r – vzdialenosť miesta, v ktorom potenciál hľadáme od náboja Q
72. Tok intenzity elektrického poľa (definícia)
Tokom T intenzity elektrického náboja E cez povrch do seba uzavretej plochy S rozumieme:
![]() , kde dS – je vektor prislúchajúci elementu
plochy dS
, kde dS – je vektor prislúchajúci elementu
plochy dS
Podľa Gaussovej – Ostrogudského vety – tok T intenzity el. poľa cez uzavretú plochu sa rovná podielu el. množstva Q nachádzajúceho sa vo vnútri plochy, a permitivity ε prostredia, v ktorom je pole vytvorené, t. j. T = Q/ε
73. Súvis intenzity a potenciálu elektrického poľa
![]()
E – intenzita, V – potenciál el. poľa
Potenciál v mieste poľa s polohovým vektorom r, v ktorom je intenzita E vzhľadom na miesto s pol. vektorom r0 môžeme počítať zo vzťahu:
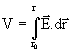
74. Gaussova veta pre elektrostatické pole (slovne aj vzorcom)
Tok vektora elektrickej intenzity ľubovoľnou uzavretou plochou sa rovná celkovému náboju, ktorý sa nachádza vnútri tejto plochy delenému permitivitou vákua
![]()
Q – celkový el. náboj nachádzajúci sa vo vnútri uzavretej plochy, dS – vektor danej uzavretej plochy, E – intenzita el. poľa, ε – permitivita prostredia v ktorom je pole vytvorené
75. Elektrické pole vo vnútri vodiča
Vo vnútri vodiča v ustálenom stave má el. potenciál všade rovnakú hodnotu, akú má na povrchu vodiča.
Podľa Gaussovej vety: vo vnútri vodiča v ustálenom stave niet vcelku el. náboja. El. náboj sídli len na povrchu vodiča.
76. Kapacita vodiča (definícia)
Kapacita vodiča C je podiel celkového náboja Q a potenciálu V vodiča teda:
![]() , [F]
, [F]
1 F – kapacita samotného vodiča na povrchu ktorého absolútny potenciál je 1 V, keď náboj telesa je 1 C
77. Kapacita sústavy dvoch vodičov (definícia)
Dva od seba izolované vodiče pri malej vzájomnej vzdialenosti predstavujú tzv. kondenzátor, t. j. zariadenie, v ktorom možno nahromadiť veľké el. náboje opačného znamienka, bez toho, že by aj rozdiel potenciálov obidvoch vodičov bol veľký.
Kapacita C je daná podielom náboja Q na jednom z obidvoch vodičov a potenciálu u tohto vodiča, vzhľadom na vodič druhý, pričom sa predpokladá, že tento vodič nesie náboj Q
![]()
Q – el. náboj, n – potenciál
78. Kapacita doskového kondenzátora
![]()
ε – permitivita, d – vzdialenosť, S – plocha dosky
79. Energia nabitého kondenzátora
![]()
C – absolútna kapacita kondenzátora, V – absolútny potenciál jednej dosky kondenzátora vzhľadom na druhú
80. Hustota energie elektrického poľa (vzorec)
![]()
W – energia v danom mieste poľa, S.d – objemová jednotka el. poľa, ε – permitivita, E – absolútna intenzita el. poľa