Introduction
The ion conductive glasses have several advantages compared to crystalline materials because of their easy preparation, the absence of grain boundaries, the isotropic properties and the large available composition variability. They can play an important role in a number of modern electrochemical devices, such as solid-state batteries, electrochronic displays, and sensors [1,2]. Therefore there is a considerable interest in the experimental study of glassy materials with the fast ion transport, particularly in their ion transport mechanisms.
The ion transport properties of many ion conducting glasses, melts and crystals are similar. The concept of relaxation is shown to provide a general basis for understanding the spectra in terms of the ion dynamics. In glassy electrolytes, the mobile ions encounter different kinds of site and the jump relaxation model has to be modified accordingly [3]. The most important criterion, which should be met by the fast ion conductive glasses, is the high ion conductivity at room temperature [3,4]. The ion transport properties of conductors are directly reflected in the electrical conductivity spectra [5]. However the transport mechanisms investigated by acoustic methods can have some advantages compared to the electrical ones as high sensitivity, absence of contact phenomena and so on [4,6].
The glasses, which contain Cu+ conductive ions, have similar electronic configuration and smaller ionic radii in comparison with Ag+ ion conducting glasses. The conductivity of glasses is affected not only by the type of conductive ions, but also strongly depends on „glass forming“ oxide. Phosphate glasses containing Cu+ conducting ions are good ionic conductors with room temperature conductivity of the order 10-3 W-1cm-1. The highest conductivity has been recorded in systems containing large fractions of cuprous halides, such as CuI or CuBr [7,8].
In this contribution we present some acoustical properties of glasses prepared in the system CuI-CuBr-Cu2O-(P2O5+MoO3).The main purpose of the contribution is to investigate ion transport mechanisms in these fast ion conductive glasses and to determine the relation between acoustical and electrical properties considering the various glass compositions.
Experiments
The procedure of glasses preparation
in the system CuI-CuBr-Cu2O-(P2O5+MoO3) from commercial reagents has been already described [6,9]. The set
of systems of glasses was originally prepared to investigate both the role of
glass-forming system and the role of cuprous halides produced Cu+
ions keeping their 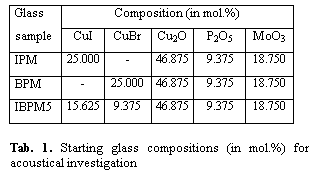 ratio 60 mol. % to 40 mol.%
[10]. However, for the acoustical attenuation measurements only three samples
were chosen (d » 2 mm), the compositions of which are
summarized in Tab. 1.
ratio 60 mol. % to 40 mol.%
[10]. However, for the acoustical attenuation measurements only three samples
were chosen (d » 2 mm), the compositions of which are
summarized in Tab. 1.
The samples for acoustical attenuation and electrical conductivity measurements were cylindrical in shape (area » 1 cm2, thickness » 2 mm).
The acoustical attenuation was measured using MATEC attenuation comparator for longitudinal acoustic wave of frequency 13, 18 and 27 MHz generated by quartz transducer. The quartz buffer was used to separate the signal from quite short sample (Fig. 1).
The frequency and temperature dependencies of electrical conductivity were measured (d.c. and a.c. in the frequency range from 50 Hz up to 1 MHz) using FLUKE PM 6306 impedance analyser in the temperature range of 140-380 K. Gold electrodes were sputtered onto the sample surfaces for electrical investigation. The measured complex impedance allowed us to obtain the bulk d.c. and a.c. conductivity of glass samples by means of the usual impedance analysis.
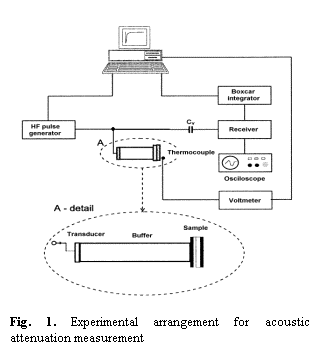
Results and discussion
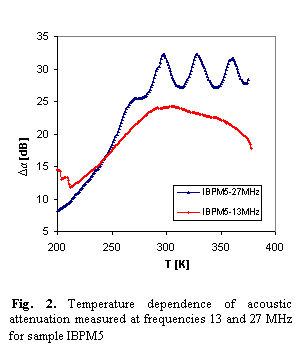
The measurements of the temperature dependence of acoustic attenuation at the frequency 13 MHz indicate in all investigated samples one broad attenuation maxima at higher temperature, in which we can distinguish at least two separated peaks. At higher frequency (18 and 27 MHz) the peaks are very well evident and at frequency 27 MHz there are even three peaks (Fig. 2).
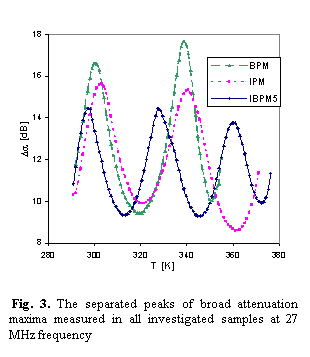
The positions of separated peaks are different for every
sample (Fig. 3) and their shift with increasing frequency is evident.
From the measured complex impedance
we obtained the bulk d.c. and a.c. conductivity of glass samples. The
temperature dependencies of d.c. conductivity indicates two transport
mechanisms with activation energies Ea1 and Ea2 for higher
and lower temperatures, respectively [10]. Activation energies calculated from
Arrhenius  plots of d.c. conductivity
are summarized in Tab. 2.
plots of d.c. conductivity
are summarized in Tab. 2.
The values of activation energies Ea2 that characterise the transport mechanisms at lower temperatures are very close because the samples contain the same molar amount of glass-forming components. The activation energies Ea1 that characterise ion transport at higher temperatures depend on the ratio of
CuI to CuBr responsible for Cu+ ion concentrations [10].
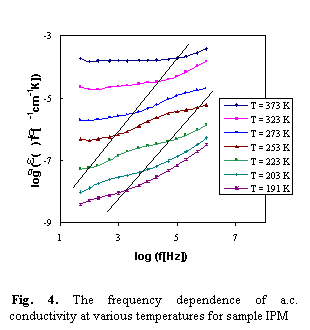
The a.c. conductivity spectra obtained from the set of frequency dependencies measured at various temperatures are illustrated in Fig. 4. The glass samples exhibits two brakes on the a.c. conductivity spectra and indicated transport hopping processes of Cu+ ions through various sites that can be explained by jump relaxation models [3]. The brakes in a.c. conductivity slopes corresponding to various transport mechanisms are shown by full lines.
The peaks at the broad maxima of acoustical attenuation
spectra (Fig. 2) indicate two possible transport mechanisms with the activation
energies very close to those determined in d.c. electric measurement. The
attenuation spectra can be explained by the assumption that temperature peaks
are caused by the diffusion processes of various kinds of ions. However,
another third mechanism is indicated by acoustic measurements comparing with
d.c. measurements.
In all glasses we studied an Arrhenius – type relaxation between the peak temperature and the applied frequency,
n = n0 exp (-Ea / kBTpeak ) , (1)
 where Ea is the activation energy,
kB is Boltzmann constant, Tpeak is the
temperature of the peak, n is frequency and n0 is preexponenial
factor. Using the activation energies calculated from the Arrhenius plots of
the d.c. conductivity and the temperature values corresponding to the peaks
that characterise measurements of acoustical attenuation at various frequencies
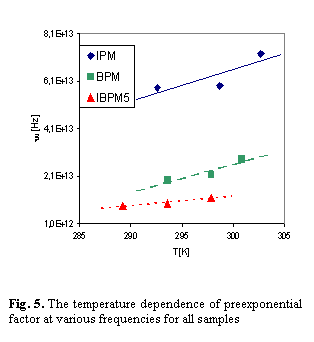
(13, 18, 27 MHz) (Tab. 3) we found the values for preexponential factor n0 (Fig. 5), which
depends on temperature.
where Ea is the activation energy,
kB is Boltzmann constant, Tpeak is the
temperature of the peak, n is frequency and n0 is preexponenial
factor. Using the activation energies calculated from the Arrhenius plots of
the d.c. conductivity and the temperature values corresponding to the peaks
that characterise measurements of acoustical attenuation at various frequencies
(13, 18, 27 MHz) (Tab. 3) we found the values for preexponential factor n0 (Fig. 5), which
depends on temperature.
We supposed that the temperature dependence of the preexponential factor is a linear function (n0=n0´T + const.). It seems, that the ratio of CuI to CuBr can be responsible for various values of the preexponential factor.
Conclusions
The experimental investigation of ion conductive glasses in system CuI-CuBr-Cu2O-(P2O5+MoO3) proved that acoustical spectroscopy can be very useful technique for transport mechanisms study and showed the coherence between the acoustical and electrical properties in fast ion conductive glasses. The influence of chemical composition on ion transport mechanisms is important too. It seems, that the same mechanisms can influence electrical and acoustical losses in ion conductive glasses.
Further investigation in wider temperature and frequency ranges of glass samples with different compositions should be done for better understanding of ion transport mechanisms and can help in finding the temperature dependence of the preexponential factor for various types of the investigated ion conducting glasses.
References
[1] M. D. Ingra: Phil. Mag. 60 (1998) 729.
[2] S. W. Martin: J. Amer. Ceram. Soc. 74 (1991) 1767.
[3] K. Funke: Sol. State Ionics 94 (1997) 27.
[4] E. V. Charnaya, B. F. Borisov, A. A. Kuleshov: Proc. World Congress on Ultrasonics, Berlin 1995, p. 483.
[5] P. Hockicko, P. Bury, M. Jamnický and I. Jamnický: Proc. of the 9th International Workshop on Appl. Phys. of Cond. Matter, Malá Lučivná 2003, p. 174.
[6] P. Bury, P. Hockicko, M. Jamnický and I. Jamnický: Proc. of the 32nd International Acoustical Conference - (EAA) Symposium, Banská Štiavnica 2002, p. 67.
[7] P. Znášik and M. Jamnický: Solid St. Ionics 95 (1997) 207.
[8] Ch. Lin and C. A. Angel: Solid St. Ionics 13 (1984) 105.
[9] T. Minami and N. Machida: Mater. Chem. Phys. 23 (1989) 63.
[10] P. Bury, P. Hockicko, M. Jamnický and I. Jamnický: Proc. 8th Int. Worshop on Appl. Phys. of Cond. Matter, Jasná 2002, p. 145.
Acknowledgements
The authors would like to thank Mr. F. Černobila for technical assistance. This work was partly financially supported by Grant 1/914/02 of the Ministry of Education of the Slovak Republic.