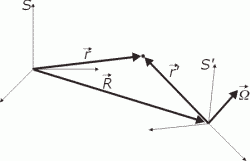
obrázok č. 1

Nech sústava S je spojená so mnou a pozerám sa na sústavu S', ktorá sa voči mne pohybuje tak, že poznám R = R(t), teda polohu jej počiatku v každom čase. Nech ešte rotuje tak, že poznám  =
=  (t). Ďalej mám časticu, ktorej poloha je určená polohovým vektorom r, resp. r'. Keby na túto časticu nepôsobili žiadne reálne sily, potom by som mal v sústave S, podľa zákona zotrvačnosti, pozorovať jej rovnomerný priamočiarý pohyb. No keď prejdem do sústavy S', ktorá môže vo všeobecnosti konať ľubovolný pohyb voči S popísaný pomocou R(t) a
(t). Ďalej mám časticu, ktorej poloha je určená polohovým vektorom r, resp. r'. Keby na túto časticu nepôsobili žiadne reálne sily, potom by som mal v sústave S, podľa zákona zotrvačnosti, pozorovať jej rovnomerný priamočiarý pohyb. No keď prejdem do sústavy S', ktorá môže vo všeobecnosti konať ľubovolný pohyb voči S popísaný pomocou R(t) a  (t), určite nebudem pozorovať rovnomerný priamočiarý pohyb tejto častice. Pri pohľade zo sústavy S' sa mi bude zdať, že na ňu pôsobia (zotrvačné) sily. Podľa obrázku č. 1 môžem pre polohu častice písať:
(t), určite nebudem pozorovať rovnomerný priamočiarý pohyb tejto častice. Pri pohľade zo sústavy S' sa mi bude zdať, že na ňu pôsobia (zotrvačné) sily. Podľa obrázku č. 1 môžem pre polohu častice písať:
Toto prepíšem cez bázové vektory sústavy S':
a zderivujem podľa času:
Aby som mohol pokračovať ďalej, budem musieť zistiť, čomu sa rovnajú časové derivácie čiarkovaných bázových vektorov podľa času. Skúsim teda rozlúštiť napríklad deriváciu di'/dt.
obrázok č. 2 | Nasledujúca úvaha sa bude opierať o obrázok č. 2. Zoberiem si infinitezimálny čas dt a zistím k nemu prislúchajúcu zmenu di'. Veľkosť tejto zmeny bude |di'| = |i'|.d |
 x i' +
x i' +  x j' +
x j' +  x k' = v' +
x k' = v' +  x r'.
x r'.Keďže chcem dostať sily, musím sa dopracovať až k zrýchleniam, a teda znovu derivovať. No teraz už viem, že pri derivovaní čiarkovaného vektora podľa času, dostanem akoby jeho deriváciu a ešte jeho vektorový súčin s vektorom  . Tento poznatok teraz využijem a dostanem:
. Tento poznatok teraz využijem a dostanem:
 x v' + E x r' +
x v' + E x r' +  x (v' +
x (v' +  x r').
x r'). x v') + E x r' +
x v') + E x r' +  x (
x ( x r'),
x r'),kde E = d /dt je úhlové zrýchlenie. Posledný výraz ešte upravím a vynásobím hmotnosťou častice:
/dt je úhlové zrýchlenie. Posledný výraz ešte upravím a vynásobím hmotnosťou častice:
ma' = ma - mA - 2m( x v') - m(E x r') - m( x v') - m(E x r') - m( x ( x ( x r')) x r')) |
Dostal som teda, že na časticu bude pôsobiť reálna sila F = ma, ktorú by som pozoroval aj v sústave S. Ďalej dobré známa zotrvačná sila Fz = -mA. Potom menej známa Corriolisova sila FC = -2m( x v'). Ešte Eulerova sila FE = -m(E x r') a nakoniec odstredivá sila Fo = -m(
x v'). Ešte Eulerova sila FE = -m(E x r') a nakoniec odstredivá sila Fo = -m( x (
x ( x r')).
x r')).
natT