systém č. 4
| < Módy | Odraz a prechod impulzu > |
Možno by si teraz čakal obrázok so štyrmi oscilátormi a ďalší spôsob riešenia problému ako popísať ich pohyb. V skutočnosti tie dva predchádzajúce spôsoby riešenia neboli rôzne. Boli to iba dva varianty realizácie tej istej myšlienky. Jeden variant si predral cestu od začiatku a druhý od konca. Priznám sa, že tu niekde, sa asi končia všetky moje tradičné vedomosti ohľadom riešenia takýchto systémov a neviem o ničom, čo by ma prinútilo riešiť štyri zviazané oscilátory na "papiery".
Nebudem riešiť štyri zviazané oscilátori ani žiaden ich konečný počet, no vyrieším nekonečné množstvo zviazaných oscilátorov.
Podľa obrázku č. 4 napíšem pohybovú rovnicu pre oscilátor v strede, podobne ako som to už robil v predchádzajúcich odsekoch. Dostávam diferenciálnu rovnicu:
Takáto rovnica platí pre každý oscilátor v nekonečnom rade oscilátorov. Teraz si premenujem výchylky oscilátorov, namiesto diskrétneho pomenovania zavediem spojité, pričom rovnovážnu vzdialenosť medzi dvoma susednými oscilátormi si označím b. Potom:
m(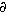 a2/ a2/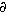 t2) = ka(x-b) - 2ka(x) + ka(x+b), t2) = ka(x-b) - 2ka(x) + ka(x+b),
| (1) |
podľa pána Taylora platí:
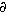 a(x)/
a(x)/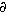 x)(-b) + (
x)(-b) + (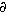 2a(x)/
2a(x)/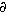 x2)(-b)2 + ..,
x2)(-b)2 + ..,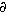 a(x)/
a(x)/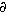 x)(+b) + (
x)(+b) + (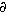 2a(x)/
2a(x)/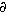 x2)(+b)2 + ..,
x2)(+b)2 + ..,to keď dosadím do (1), tak dostanem vlnovú rovnicu:
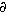 2a(x,t)/
2a(x,t)/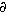 t2) = kb2(
t2) = kb2(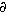 2a(x,t)/
2a(x,t)/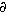 x2).
x2).Táto rovnica predstavuje parciálnu diferenciálnu rovnicu pre funkciu a = a(x,t). Keď si zavediem označenie v2 = kb2/m, potom ju môžem prepísať prehladnejšie:
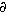 2a/ 2a/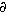 t2 = v2 t2 = v2 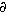 2a/ 2a/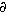 x2. x2.
| (3) |
Dosadením sa môžeš presvedčiť, že riešeniami rovnice (3) sú všetky funkcie typu:
a = f(t  x/v), x/v),
| (4) |
teda také funkcie, ktoré sa pohybujú rýchlosťou v smerom doprava alebo doľava, pričom sa nemení ich tvar. Z toho vyplýva, že mechanické vlnenie v nekonečnom rade oscilátorov sa bude šíriť rýchlosťou:
v = b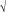 (k/m), (k/m),
| (5) |
kde b je rovnovážna vzdialenosť medzi oscilátormi o hmotnosti m a k je koeficient pružnosti pružín medzi nimi.
Ešte treba upozorniť na najpoužívanejšie riešenie rovnice (3), a tým je nekonečná monochromatická vlna s frekvenciou  = 2
= 2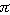 f:
f:
a(x,t) = Asin[ (t - x/v)] = Asin( (t - x/v)] = Asin( t - t -  x/v) = Asin( x/v) = Asin( t - dx), t - dx),
| (6) |
pričom
d =  /v = 2 /v = 2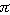 /(Tv) = 2 /(Tv) = 2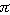 / / , ,
| (7) |
kde  = vT je vlnová dĺžka monochromatickej vlny.
= vT je vlnová dĺžka monochromatickej vlny.
by natT
| < Módy | Odraz a prechod impulzu > |