Harmonick² oscilßtor

systΘm Φ. 1

Prv² systΘm pozostßva z Φastice o hmotnosti m, ktorß je prichytenß na pru╛inku. ╚astica sa nachßdza v rovnovß╛nej polohe, neh²be sa. Ak jej udelφ╣ impulz, naru╣φ╣ t·to rovnovßhu a na Φasticu zaΦne p⌠sobi╗ pru╛inka. Bude p⌠sobi╗ silou, a to tak, ╛e sa bude sna╛i╗ vrßti╗ ju spΣ╗ do rovnovß╛nej polohy. Klikni na obrßzok hore, udel Φastici impulz a uvidφ╣, Φo sa bude dia╗ pri p⌠sobenφ takejto sily.

V d⌠sledku sφl, ktor²ch v²slednica p⌠sobφ proti v²chylke z rovnovß╛nej polohy, teda nastßva kmitanie. Ako to v╣ak zapφsa╗ matematicky? Dß sa to urobi╗ mnoh²mi sp⌠sobmi, no najjednoduch╣φm, a pritom dostatoΦne pravdiv²m, je tento: F ~ -x (x je klasickß s·radnica s nulou v rovnovß╛nej polohe). V reΦi slov: velkos╗ v²slednej sily p⌠sobiacej na Φasticu je lineßrne ·mernß v²chylke a je orientovanß opaΦne.

Pre ·plnos╗ mi e╣te ch²ba kon╣tanta ·mernosti - oznaΦφm ju k a pomenujem koeficient pru╛nosti, ktor² v na╣om prφpade charakterizuje tuhos╗ pru╛inky, resp. pru╛nos╗ materißlu, z ktorΘho je vyrobenß. Teda:

Z Newtonovho pohybovΘho zßkona, potom dostanem tak·to rovnicu pre pohyb Φastice:

kde x(t) je funkcia polohy zßvislß od Φasu, priΦom x''(t) je jej druhß derivßcia pod╡a Φasu, a platφ x'' = a. Neznßmou v tejto rovnici je teda funkcia x(t), ktor· ke∩ nßjdem, tak som zistil polohu Φastice v ka╛dom Φase, teda som popφsal jej pohyb. Tßto rovnica sa tie╛ volß diferencißlna a ke∩ chcem nßjs╗ jej konkrΘtne rie╣enie, musφm zada╗ poΦiatoΦnΘ podmienky, tj. polohu Φastice a jej r²chlos╗ v nejakom konkrΘtnom Φase. My sme v Φase t = 0 udelili Φastici v jej rovnovß╛nej polohe urΦit² impulz, teda r²chlos╗ v₀, a preto platφ:

Rie╣enie diferencißlnej rovnice (1a) pre poΦiatoΦnΘ podmienky (1b) je (pozri prφklad Φ. 1):

x(t) = Asin(2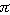t/T),

(2)

A = v0(m/k)1/2, T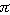 = 2(m/k)1/2,

(2a,b)

kde A je maximßlna v²chylka, ktor· Φastica dosiahne - amplit·da. T je peri≤da, typick² Φas pre danΘ usporiadanie, priΦom platφ x(t) = x(t + T), Φo znamenß, ╛e pohyb sa periodicky opakuje a do toho istΘho bodu sa Φastica dostane za Φas T.

Preto╛e na Φasticu p⌠sobφ v²slednß sila (1), a preto╛e sφnus je harmonickß funkcia, takΘto kmitanie volßme lineßrne alebo harmonickΘ a pre nekor╣ie ·Φely bude e╣te v²hodnΘ zisti╗, akß je mechanickß energia Φastice, ktorß konß harmonick² kmitav² pohyb. Ke∩╛e na zaΦiatku bola Φastica v pokoji, jej mechanickß energia (kinetickß + potencißlna) bola nulovß. Tvojφm ·derom do Φastice si jej udelil urΦit· poΦiatoΦn· r²chlos╗ v₀, teda kinetick· energiu T:

Ke∩ si vyjadrφm v₀ zo vz╗ahu (2a) a dosadφm to do poslednΘho v²razu (3a), dostanem u╛itoΦnej╣φ tvar:

Toto platφ pre kinetick· energiu Φastice tesne po tvojom impulze. No ke∩╛e platφ zßkon zachovania energie pre izolovanΘ s·stavy, platφ to aj pre celkov· mechanick· energiu Φastice poΦas celΘho jej pohybu:

Ke∩ to v╣etko zhrniem - ak na Φasticu p⌠sobφ v²slednß sila F = -kx, potom pri poΦiatoΦn²ch podmienkach (1b) sa bude pohybova╗ tak, ╛e x(t) = Asin(2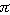t/T) s celkovou mechanickou energiou E = ¹/₂ kA². Tak²to pohyb volßme harmonick² kmitav² pohyb.

by natT

Prφklady

Vyzerß to v╣etko jednoducho, no Φi tomu naozaj rozumie╣, sa bude╣ m⌠c╗ presvedΦi╗ na nasleduj·cich dvoch krßtkych prφkladoch.

obrßzok Φ. 1

1. Zadanie: Zisti ako sa bude pohybova╗ Φastica v systΘme na obrßzku Φ. 1 pri ╡ubovoln²ch poΦiatoΦn²ch podmienkach. In²mi slovami - rie╣ diferencißlnu rovnicu (1a) pri tak²chto poΦiatoΦn²ch podmienkach:

Rie╣enie: Najprv si rovnicu (1a) upravφm na tvar:

Teraz vidφm, ╛e mojou ·lohou je nßjs╗ tak· funkciu x(t), ktor· ke∩ dvakrßt zderivujem, tak dostanem t· ist² funkciu s opaΦn²m znamienkom a╛ na kon╣tantu k/m - t· si kv⌠li zjednodu╣enie ∩al╣ieho zßpisu oznaΦφm ². Mßm teda rovnicu pre funkciu x(t):

x''(t) = -2x(t).

Funkcie, ktorΘ spσ≥aj· t·to rovnos╗, mi napadn· hne∩ dve, a to sin(t) a cos(t). Lebo po dvoch derivovaniach sa zmenφ znamienko, funkcie zostan· a potrebnß kon╣tanta so dostane von. Ke∩ si premyslφm, ako sa tieto dve funkcie derivuj· v mojej rovnici, zistφm, ╛e rie╣enφm m⌠╛e by╗ aj ╡ubovolnß kombinßcia t²chto funkciφ:

x(t) = Asin(t) + Bcos(t),

kde A a B s· ╡ubovolnΘ reßlne kon╣tanty. A to je presne to, Φo potrebujem. Na╣iel som rie╣enie s dvoma neznßmymi kon╣tantami a mßm dve znßme poΦiatoΦnΘ podmienky. Dosadφm poΦiatoΦnΘ podmienky (teda v Φase t = 0):

x(0) = Asin(.0) + Bcos(.0),

v(0) = x'(0) = Acos(.0) - Bsin(.0),

a dostanem:

v₀ = A.

Teda hladanΘ rie╣enie je:

x(t) = (v₀/)sin(t) + x₀cos(t),

kde = (k/m)^1/2.

2. Zadanie: Predstav si dva systΘmy - jeden pod╡a obrßzku Φ. 2a a druh² pod╡a obrßzku Φ. 2b. Prezradφm ti, ╛e Φastice v oboch systΘmoch bud· kona╗ harmonick² kmitav² pohyb (premysli si to). Tvojou ·lohou bude vyjadri╗ kon╣tanty tuhosti t²chto systΘmov pomocou kon╣tßnt k₁ a k₂.

obrßzok Φ. 2a	obrßzok Φ. 2b

Rie╣enie: Sk·s sa potrßpi╗ a napφ╣ mi tvoj nßzor. V dohladnej dobe uvediem samozrejme aj rie╣enie.

by natT