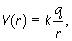
Volám sa Milan a budem riešiť jeden z ukážkových príkladov z elektriny. Pri riešení budem používať matematický aparát, ktorý si vyžaduje vedomosti prváka na vysokej (tým však nechcem odradiť nažhaveného stredoškoláka). Zaujímavé na tomto príklade je to, že pre bežného "smrtelníka" nie je riešitelný priamočiaro, no bude riešitelný, keď trochu pozmením zadanie a použijem trik známy ako metóda imaginárneho náboja.
Zadanie: Vo vodivej uzemnenej sfére o polomere a je umiestnený náboj
q vo vzdialenosti d od stredu sféry (pozri Obr.1).
Vypočítaj:
a) aká sila pôsobí na náboj velkosti q?
b) aký potenciál je vo vnútri vodiča?
c) ako sa rozloží náboj na vnútornej stene vodiča?
Riešenie: Skôr ako začnem riešiť bod a), bude treba urobiť následujúcu úvahu: Vodič je uzemnený, to znamená, že všetok náboj z povrchu je odvádzaný preč. Preto náboj q vo vnútri (vodiča) nemôže nijako ovplyňovať elektrické pole vonku. Pre jednoduhosť budem považovať elektrické pole mimo vodiča za nulové, a potom, kedže vonku nie je elektrické pole, nebude vykonávaná žiadná práca pri prenášaní náboja z nekonečna na povrch vodiča. Práca je rozdiel potenciálov, preto potenciál na vodiči je rovnaký ako v nekonečne (povrch vodiča je ekvipotenciálna plocha). Ak budem potenciál V rátať pomocou vzorca:
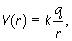 |
(1) |
(k je konštanta úmernosti) potom potenciál v nekonečne, teda aj na vodiči, bude nulový.
Teraz na chvíľu preruším túto úvahu a pozriem sa na Obr.2. Sú tam ekvipotenciálne hladiny dvoch opačne nabitých nábojov v ich rovine. Pre veľkosti nábojov platí: |qvpravo| = 2|qvľavo|. Kladné hodnoty potenciálu sú vynesené červenou farbou, záporné modrou. A teda na rozhraní modrej a červenej sa nachádza nulový potenciál. Toto rozhranie sa na obrázku podobá na kružnicu. A čo ak to je kružnica? A čo ak to je v priestore sféra? Potom by som mohol do tohoto rozhrania vložiť vodivú uzemnenú sféru (teda s nulovým potenciálom) určitých rozmerov a vôbec by neovplyvnila vzájomne pôsobenie medzi týmito nábojmi.
Presne to teraz využijem a pozriem sa na ďaľší obrázok - Obr.3. Na ňom možno vidieť siločiary tých istých nábojov a uzemnený vodič, ktorý teda svojou prítomnosťou nemení elektrické pole od týchto dvoch nábojov. Siločiary sú z definície kolmé na ekvipotenciálne plochy a teda aj na vodič. Teraz je už zrejmé (okrajové podmienky), že v okolí náboja qvľavo bude rovnaké elektrické pole, či naň pôsobí imaginárny náboj qvpravo, alebo uzemnený vodič. A teda môžem si úlohu pôsobenia vodiča na náboj premeniť na úlohu o pôsobení náboja na náboj.
To je všetko pekné, no neuverím tomu, kým to nespočítam. Začnem tým, že nájdem ekvipotenciálnu plochu dvoch opačne nabitých, ináč ľubovoľných nábojov q a q'. Pre určitosť si zvolím náboj q záporný a náboj q' kladný. Súradnicovú sústavu a ostatné označenia si zavediem podľa Obr.1 a Obr.4 (Os x je červená, y zelená a z modrá.) A počítam:
Potenciál V od náboja q v ľubovolnom bode priestoru bude:
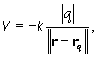 |
(2a) |
kde rq je poloha náboja q. Podobne potenciál V' od náboja q':
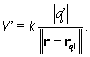 |
(2b) |
(Pripomínam, že náboj q' som si zvolil kladný.)
Chcem nájsť nulovú ekvipotenciálnu hladinu, teda chcem zistiť, kde ležia body, ktoré spĺňajú: V + V' = 0. Postupne dostanem:
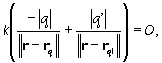 |
(3a) |
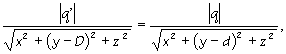 |
(3b) |
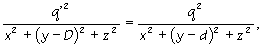 |
(3c) |
| ... | |
 |
(3d) |
kde
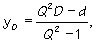 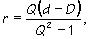 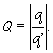 |
(3e) |
Takže hladina nulového potenciálu je naozaj sférou so stredom v bode [0, y0, 0] a s polomerom r, ako som očakával. Teraz však musím nastaviť veľkosť a vzdialenosť imaginárneho náboja q' tak, aby mi hladina nulového potenciálu (medzi q a q') presne sadla na moju sféru zo zadania.
Z voľby súradníc vyplýva, že musím položiť: y0 = 0 a r = a, potom:
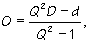 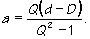 |
(4a) |
Riešením týchto podmienok dostanem hľadanú polohu a veľkosť imaginárneho náboja:
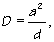 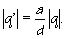 |
(4b) |
A teraz mi už nič nebrání počítať túto úlohu ako úlohu o pôsobení dvoch nábojov.
a) Z Coulombového zákona náboj q' (a teda vodič) pôsobí na náboj q silou:
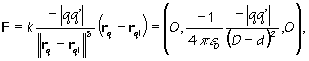 |
(5a) |
využitím (4b), odpoveď na otázku a) bude:
 |
(5b) |
b) Keď už viem veľkosť imaginárneho náboja a jeho umiestnenie, potom je odpoveď na b) jednoduchá, stačí mi v priestore sféry sčítať potenciály (2a) a (2b) od oboch nábojov.
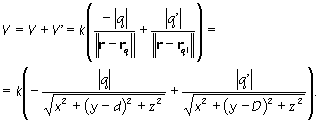 |
(6a) | |
S využitím (4b) dostanem odpoveď na otázku b):
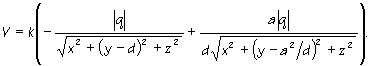 |
(6b) | |
Približnú predstavu o tom, ako to vyzerá pre |q'| = 2|q|, d = 1 a D = 5, možno získať z Obr.6a,b,c,d, kde je načrtnutá funkcia V(x, y) v rovine nábojov. (Rozhranie modrej a červenej zodpovedá umiestneniu vodiča.)
c) Zistiť, ako sa rozloží náboj na vnútornej stene vodiča, už nebude také
jednoduché. Najprv si musím uvedomiť, že rozloženie elektrického náboja na ploche
mi charakterizuje fyzikálna veličina 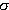 - plošná hustota náboja, ktorej definícia je:
- plošná hustota náboja, ktorej definícia je:
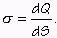 |
(7) |
Z tohoto vyjadrenia veľa toho nevypočítam a aby som získal lepšie, budem musieť použiť Gaussov zákon, ktorý hovorí: Tok elektrickej intenzity E cez uzavretú plochu S je úmerný celkovému náboju vo vnútri tejto plochy - Q, teda:
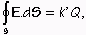 |
(8) |
kde k' je konštanta úmernosti.
Plocha, ktorú som si zvolil pre Gaussov zákon, má tvar "plechovky" (pozri Obr.7). Výšku plechovky si zvolím veľmi (infinitezimálne) malú. To znamená takú malú, že ju bude možné zanedbať v porovnaní s rozmermi sféry (aj keď na obrázku to tak nevyzerá). Potom budem môcť považovať tok vektora E bočnými stenami za nulový. Podstavu plechovky si zvolím opäť infinitezimálne malú (celá podstava bude rovnobežná s povrchom sféry). Mimo vodiča nie je žiadne elektrické pole, preto tok elektrickej intenzity podstavou mimo vodiča bude nulový. Tok vnútornou podstavou bude: EdS (E je veľkosť vektora E a dS je veľkosť infinitezimálnej plôšky, ktorou vektor E prechádza kolmo).
Celkový tok elektrickej intenzity E mojou plechovkou teda bude:
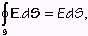 |
(9) |
(vektor dS smeruje vždy von z uzavretej plochy) no tento tok je úmerný (Gaussov zákon) celkovému náboju vo vnútri
plechovky, ktorý sa nachádza na infinitezimálnej plôške veľkosti dS z vnútra
sféry. Keďže táto plôška je veľmi malá, môžem predpokladať, že je na nej náboj
rozmiestnený rovnomerne, a potom môžem priamo použiť definíciu plošnej hustoty
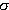 (7) na vyjadrenie tohoto náboja:
(7) na vyjadrenie tohoto náboja:
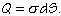 |
(10) |
Dosadením (9) a (10) do Gaussovho zákona (8) dostanem:
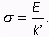 |
(11) |
Dostal som tak užitočnejšie vyjadrenie pre plošnú hustotu náboja 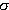 ,
ktoré mi hovorí, že ak chcem zistiť rozloženie náboja na sfére, musím vlastne zistiť
rozloženie veľkosti elektrickej intenzity E. A teraz mi nepomôže už nič iné,
iba začať rátať:
,
ktoré mi hovorí, že ak chcem zistiť rozloženie náboja na sfére, musím vlastne zistiť
rozloženie veľkosti elektrickej intenzity E. A teraz mi nepomôže už nič iné,
iba začať rátať:
Najprv zistím, aká je intenzita E v ľubovolnom bode sféry (xs, ys, zs). To zistím jednoduchým sčítaním (pozri Obr.8) intenzít E1 a E2 od nábojov q a q' v bode (xs, ys, zs):
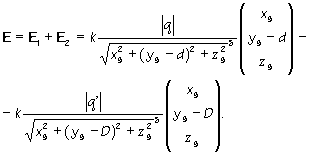 |
(12) |
(Ešte raz pripomínam, že náboj q je kladný a q' záporný.)
Mňa ale zaujíma veľkost vektora elektrickej intenzity. Veľkosť vektora dostanem napríklad tak, že ho skalárne prenásobím jednotkovým vektorom, ktorý má rovnaký smer ako daný vektor. Kedže vektor E je kolmý na sféru s počiatkom v bode [0, 0, 0], môžem jeho veľkosť určiť tak, že ho skalárne prenásobím jednotkovým radiálnym vektorom nr (pozri Obr.9):
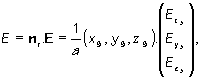 |
(13a) |
keď teraz dosadím (12) do tohoto vyjadrenia dostanem:
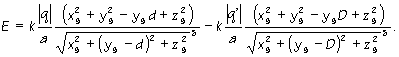 |
(13b) |
Tým je bod c) prakticky vyriešený. Stačí už iba dosadiť posledný výraz do
(11). Dostal by som však plošnú hustotu 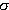 ako funkciu troch premenných: xs, ys,
zs. Kedže však popisujem rozloženie náboja na ploche, potom
určite existujú také súradnice, v ktorých možno napísať
ako funkciu troch premenných: xs, ys,
zs. Kedže však popisujem rozloženie náboja na ploche, potom
určite existujú také súradnice, v ktorých možno napísať 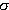 ako funkciu
dvoch premenných. Takými súradnicami sú napríklad také ako na Obr.10.
Podľa tohoto obrázka platí:
ako funkciu
dvoch premenných. Takými súradnicami sú napríklad také ako na Obr.10.
Podľa tohoto obrázka platí:
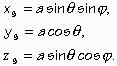 |
(14) |
Dosadením týchto transformačných vzťahov do (13b) dostanem:
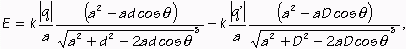 |
(13c) |
po využití (4b) a po úprave:
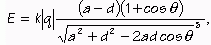 |
(13d) |
a teda pre plošnú hustotu elektrického náboja na sfére podľa (11):
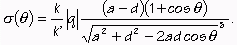 |
(15) |
Nakoniec vyšla 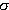 ako funkcia iba jednej premennej. Čo sa dalo
v tomto prípade čakať, pretože úloha je symetrická vzhľadom na os, ktorá prechádza
nábojmi q a q'. Každá symetria znamená zjednodušenie a v tomto prípade
ako funkcia iba jednej premennej. Čo sa dalo
v tomto prípade čakať, pretože úloha je symetrická vzhľadom na os, ktorá prechádza
nábojmi q a q'. Každá symetria znamená zjednodušenie a v tomto prípade
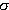 nezávisí od
nezávisí od 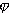 .
.
Názorne možno vidieť rozloženie elektrického náboja na vodivom uzemnenom vodiči v tvare sféry na obrázku Obr.11 pre d/a = 1/4 (zelená), d/a = 1/2 (červená) a d/a = 3/4 (modrá).
Ak máš dajaké otázky, pripomienky, alebo mám niekde chybu kľudne mi napíš na natt@pobox.sk
by natT (29.12.2001)