Mokré koleso
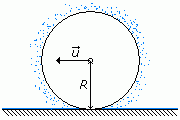
Zadanie: Po mokrej ceste sa rýchlosťou velkosti u valí koleso o polomere R. Do akej maximálnej výšky môže vyletieť kvapka, ktorá sa odtrhne od kolesa?
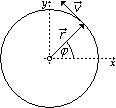
obrázok č. 1
Riešenie: Na obrázku č. 1 môžeš vidieť, že som si zvolil vzťažnú sútavu spojenú so stredom kolesa. Pre také označenie, aké som si zvolil na obrázku, môžem pre polohu konkrétneho bodu na obvode kolesa písať:
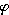 , Rsin
, Rsin 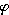 ),
),kde 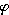 sa mení rovnomerne s časom t podľa vzťahu
sa mení rovnomerne s časom t podľa vzťahu 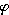 =
=  t, pričom platí
t, pričom platí  = u/R. Derivovaním podľa času dostanem rýchlosť daného bodu:
= u/R. Derivovaním podľa času dostanem rýchlosť daného bodu:
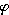 , ucos
, ucos 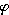 ).
).Teraz budem predpokladať, že z ľubovolného miesta na obvode kolese sa odtrhne kvapka. Potom vypočítam výšku, do akej vyletí a nakoniec zistím, pri akom 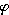 bude táto výška maximálna. Koleso sa pohybuje doľava, teda smerom nahor budú vytrhávané kvapky, pre ktoré platí -
bude táto výška maximálna. Koleso sa pohybuje doľava, teda smerom nahor budú vytrhávané kvapky, pre ktoré platí -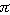 /2 <
/2 < 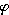 <
< 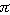 /2. Budú sa pohybovať v homogénnom gravitačnom poli, a pretože ma zaujíma iba výška, do ktorej vyletia, budú mi na to stačiť tieto vzťahy z kinematiky:
/2. Budú sa pohybovať v homogénnom gravitačnom poli, a pretože ma zaujíma iba výška, do ktorej vyletia, budú mi na to stačiť tieto vzťahy z kinematiky:
vy = vy0 - gt
kde y0 je súradnica miesta, z ktorého kvapka vyletí a vy0 je zložka rýchlosti, ktorou vyletí. Platí:
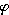 ,
,vy0 = ucos
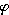 .
.(-
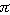 /2 <
/2 < 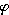 <
< 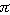 /2)
/2)Ďalej vypočítam čas, kedy bude rýchlosť vy nulová, a ten dosadím do vzťahu pre y. Dostanem tak výšku, do ktorej kvapka vyletí v závislosti od miesta, z ktorého vyletela:
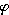 + (u2/2g)cos2
+ (u2/2g)cos2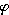 .
.Túto rovnosť zderivujem podľa 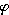 a dostanem miesto, z ktorého kvapky vylietávajú najvyššie. Po zderivovaní:
a dostanem miesto, z ktorého kvapky vylietávajú najvyššie. Po zderivovaní:
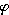 )(R - (u2/g)sin
)(R - (u2/g)sin 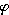 ),
),z toho dostanem podmienky:
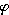 ,
,Rg/u2 = sin
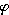 .
.Prvá podmienka bude splnená vždy, pre 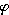 =
= 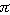 /2, druhá iba vtedy, ak bude platiť Rg/u2 < 1. To znamená, že ak bude rýchlosť kolesa u vačsia ako
/2, druhá iba vtedy, ak bude platiť Rg/u2 < 1. To znamená, že ak bude rýchlosť kolesa u vačsia ako 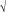 (Rg), musím maximálnu výšku rátať z podmienky č. 2 a kvapky vyletia aj vyššie ako 2R, v opačnom prípade mi z podmienky č. 1 vyplýva, že kvapky sa dostanú najviac do výšky 2R. Stručne zapísané:
(Rg), musím maximálnu výšku rátať z podmienky č. 2 a kvapky vyletia aj vyššie ako 2R, v opačnom prípade mi z podmienky č. 1 vyplýva, že kvapky sa dostanú najviac do výšky 2R. Stručne zapísané:
hmax = 2R, pre u  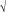 (Rg), (Rg), hmax = R + u2/2g + gR2/2u2, pre u  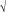 (Rg) (Rg) |
by natT