Goniometrické funkcie
|
Vz»ahy medzi funkciami Funkcie súčtu a rozdielu Súčty a rozdiely funkcií Súčiny funkcií Funkcie násobkov uhlov |
Základný vz»ah:
Vz»ahy medzi funkciami
i) eiae-ia = (cosa + isina)(cosa - isina) = cos2a + sin2a = 1ii) tg2a + 1 = (cos2a + sin2a)/cos2a = 1/cos2a
| Funkcia | sina | cosa | tga | cotga |
| sina= | sina |  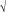 (1-cos2a) (1-cos2a)
|  tga/ tga/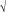 (1+tg2a) (1+tg2a)
|  1/ 1/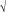 (1+cotg2a) (1+cotg2a)
|
| cosa= |  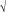 (1-sin2a) (1-sin2a)
| cosa |  1/ 1/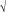 (1+tg2a) (1+tg2a)
|  cotga/ cotga/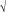 (1+cotg2a) (1+cotg2a)
|
| tga= |  sina/ sina/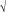 (1-sin2a) (1-sin2a)
|  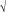 (1-cos2a)/cosa (1-cos2a)/cosa
| tga | 1/cotga |
| cotga= |  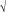 (1-sin2a)/sina (1-sin2a)/sina
|  cosa/ cosa/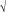 (1-cos2a) (1-cos2a)
| 1/tga | cotga |
Funkcie súčtu a rozdielu
ei(a+b) = eiaeibcos(a+b) + isin(a+b) = (cosa + isina)(cosb + isinb) =
= cosacosb - sinasinb + i(cosasinb + sinacosb)
sin(a  b) = cosasinb b) = cosasinb  sinacosb sinacosb
| sin(2a) = 2sinacosa |
| sin2(a/2) = (1 - cosa)/2 | |
cos(a  b) = cosacosb b) = cosacosb  sinasinb sinasinb
| cos(2a) = cos2a - sin2a |
| cos2(a/2) = (1 + cosa)/2 | |
tg(a  b) = (tga b) = (tga  tgb)/(1 tgb)/(1  tgatgb) tgatgb)
| tg(2a) = 2tga/(1 - tg2a) |
| tg2(a/2) = (1 - cosa)/(1 + cosa) | |
cotg(a  b) = (cotgacotgb b) = (cotgacotgb  1)/(cotgb 1)/(cotgb  cotga) cotga)
| cotg(2a) = (cotg2a - 1)/(2cotga) |
| cotg2(a/2) = (1 + cosa)/(1 - cosa) |
Súčty a rozdiely funkcií
cos(a + b) + cos(a - b) = cosacosb - sinasinb + cosacosb + sinasinb == 2cosacosb = |substitúcia a = (x + y)/2, substitúcia b = (x - y)/2| =
= 2cos[(x + y)/2]cos[(x - y)/2] = cosx + cosy
| sina + sinb = 2sin[(a + b)/2]cos[(a - b)/2] |
| sina - sinb = 2cos[(a + b)/2]sin[(a - b)/2] |
| cosa + cosb = 2cos[(a + b)/2]cos[(a - b)/2] |
| cosa - cosb = -2sin[(a + b)/2]sin[(a - b)/2] |
tga  tgb = sin(a tgb = sin(a  b)/(cosacosb) b)/(cosacosb)
|
cotga  cotgb = sin(b cotgb = sin(b  a)/(sinasinb) a)/(sinasinb)
|
tga  cotgb = cotgb =  cos(a cos(a  b)/(cosasinb) b)/(cosasinb)
|
Súčiny funkcií
cos(a - b) - cos(a + b) = cosacosb + sinasinb - cosacosb + sinasinb == 2sinasinb
| sinasinb = [cos(a - b) - cos(a + b)]/2 |
| cosacosb = [cos(a - b) + cos(a + b)]/2 |
| sinacosb = [sin(a + b) + sin(a - b)]/2 |
| tgatgb = (tga + tgb)/(cotga + cotgb) |
| cotgacotgb = (cotga + cotgb)/(tga + tgb) |
| tgacotgb = (tga + cotgb)/(cotga + tgb) |
Funkcie násobkov uhlov
e3ia = (eia)3(cos3a + isin3a) = (cosa + isina)3
cos3a + isin3a = cos3a + 3icos2asina + 3i2cosasin2a + i3sin3a
cos3a + isin3a = cos3a - 3cosasin2a + i(3cos2asina + sin3a)
| sin3a = 3sina - 4sin3a |
| sin4a = 8sinacos3a - 4sinacosa |
| sin5a = 16sinacos4a - 12sinacos2a + sina |
| sinna = nsinacosn-1a - C(3,n)sin3acosn-3a + C(5,n)sin5acosn-5a - .. |
| cos3a = 4cos3a - 3cosa |
| cos4a = 8cos4a - 8cos2a + 1 |
| cos5a = 16cos5a - 20cos3a + 5cosa |
| cosna = cosna - C(2,n)sin2acosn-2a + C(4,n)sin4acosn-4a - .. |
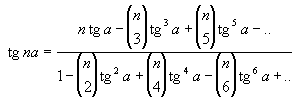
|
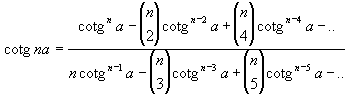
|