- vektor hodn⌠t nezßvisle premennej veliΦiny, dσ╛ky n
- vektor nameran²ch hodn⌠t, dσlky n
- vektor aproximovan²ch hodn⌠t, dσ╛ky n
- vektor neznßmych parametrov, dσ╛ky k- vektor hodn⌠t nezßvisle premennej veliΦiny, dσ╛ky n
- vektor nameran²ch hodn⌠t, dσlky n
- vektor aproximovan²ch hodn⌠t, dσ╛ky n
- vektor neznßmych parametrov, dσ╛ky k
F - matica funkΦn²ch hodn⌠t, ve╡kosti 
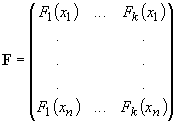
Napr. pre lineßrnu regresiu 1. rßdu (t.j. pre nßhradu nameran²ch hodn⌠t priamkou) je
a matica F mß rozmer nx2.
AproximovanΘ hodnoty pre dan· maticu funΦn²ch hodn⌠t F a parametre b zφskame ako
Potom odch²lka nameran²ch hodn⌠t od aproximovan²ch hodn⌠t je vektor
╧alej kvadrßt odch²lky je
Aby bolo splnenΘ kritΘrium minima kvadrßtu odch²lky, musφ plati╗
Z toho vypl²va, ╛e
a teda
je h╡adan² vektor neznßmych parametrov.
E