 - pozri obrázok dole). Bude pozorovateľ, ktorý zachytí tento fotón pozorovať rovnakú frevenciu? Zo zákonov zachovania energie a hybnosti ti ukážem, že nie!
- pozri obrázok dole). Bude pozorovateľ, ktorý zachytí tento fotón pozorovať rovnakú frevenciu? Zo zákonov zachovania energie a hybnosti ti ukážem, že nie!Predstav si atóm o hmotnosti M pohybujúci sa rýchlosťou v (vo vzťažnej sústave pozorovateľa), ktorý vyžiarí fotón s frekvenciou f (pod uhlom  - pozri obrázok dole). Bude pozorovateľ, ktorý zachytí tento fotón pozorovať rovnakú frevenciu? Zo zákonov zachovania energie a hybnosti ti ukážem, že nie!
- pozri obrázok dole). Bude pozorovateľ, ktorý zachytí tento fotón pozorovať rovnakú frevenciu? Zo zákonov zachovania energie a hybnosti ti ukážem, že nie!
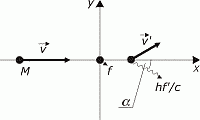
Najjednoduchšie sa táto nutná zmena frekvencie ukáže tak, že budem uvažovať vyžiarenie fotónu v smere vektora v (pre  = 0). Takto vyžiarenému fotónu zodpovedá hybnosť p = E/c, kde E je jeho energia (pozri Súvis medzi energiou a hybnosťou). Potom zo zákona zachovania hybnosti vyplýva, že po vyžiarení sa musí hybnosť atómu, a teda aj jeho kinetická energia, zmenšiť. Táto energia, ktorú atóm stratí, zo zákonu zachovania energie pripadne fotónu. Energia fotónu sa teda zvýši, a tým sa zvýši aj jeho frekvencia, lebo platí f = E/h, kde h je Planckova konštanta.
= 0). Takto vyžiarenému fotónu zodpovedá hybnosť p = E/c, kde E je jeho energia (pozri Súvis medzi energiou a hybnosťou). Potom zo zákona zachovania hybnosti vyplýva, že po vyžiarení sa musí hybnosť atómu, a teda aj jeho kinetická energia, zmenšiť. Táto energia, ktorú atóm stratí, zo zákonu zachovania energie pripadne fotónu. Energia fotónu sa teda zvýši, a tým sa zvýši aj jeho frekvencia, lebo platí f = E/h, kde h je Planckova konštanta.
Teraz teda všeobecne. Podľa obrázku hore bude zákon zachovania hybnosti znieť:
smer osi x: p = p'x + (hf'/c)cos , ,smer osi y: 0 = p'y + (hf'/c)sin  , , | (1) |
kde p = Mv. Zmena kinetickej energie atómu je:
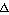 T = T' - T = (p'2 - p2)/2M. T = T' - T = (p'2 - p2)/2M. |
Pomocou vzťahov (1) si môžem vyjadriť p'2 = (p'x)2 + (p'y)2 a dostanem:
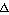 T = [-2p(hf'/c)cos T = [-2p(hf'/c)cos + (hf'/c)2]/2M. + (hf'/c)2]/2M. |
Druhý člen súčtu (h2f'2/2Mc2) v poslednom vzťahu je v bežných situáciach zanedbatelný, preto pre zmenu kinetickej energie môžem písať:
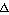 T = -hf'(v/c)cos T = -hf'(v/c)cos . . | (2) |
Nakoniec mi ešte zostáva napísať zákona zachovania energie pre moju situáciu:
hf = hf' + 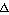 T, T, | (3) |
po dosadení (2) do (3) dostanem výsledok:
f' = f/[1 - (v/c)cos ] ~ f[1 + (v/c)cos ] ~ f[1 + (v/c)cos ] ] |
pričom posledné priblíženie, kedy v << c, je nutné, keďže som neuvažoval relativisticky.
natT