 , ktorou sa potom od neho šíri vlnenie (zvuk). Ak sa toto vlnenie širi rýchlosťou c (napr. v atmosfére pri povrchu je to približne 330 m.s-1), potom platí:
, ktorou sa potom od neho šíri vlnenie (zvuk). Ak sa toto vlnenie širi rýchlosťou c (napr. v atmosfére pri povrchu je to približne 330 m.s-1), potom platí:Tento jav budem kvôli lepšej predstave popisovať na akustickom vlnení v atmosfére, pričom budem hovoriť o zdroji zvuku (na obrázkoch značený ako Z) a o pozorovateľovi, alebo keď chceš o poslucháčovu (na obrázkoch ako P). Mojou úlohou bude zistiť, ako vníma pozorovateľ určitý tón, ktorý vysiela zdroj, keď sa pohybujú rovnomerným pohybom voči povrchu Zeme, pričom budem predpokladať, že vzduch je voči povrchu Zeme nehybný.
Začnem od najjednoduchšieho prípadu, od relatívneho pohybu pozorovateľa a zdroja pozdĺž priamky. Neskôr sa pozriem aj na všeobecný pohyb, tzn. v priestore sa bude pozorovateľ aj zdroj zvuku pohybovať ľubovolným smerom.
Kým začnem, pripomeniem ti jednu variantu vzťahu s = vt. Je to vzťah medzi periódou kmitania zdroja TZ (resp. jeho frekvenciou fZ) a vlnovou dĺžkou  , ktorou sa potom od neho šíri vlnenie (zvuk). Ak sa toto vlnenie širi rýchlosťou c (napr. v atmosfére pri povrchu je to približne 330 m.s-1), potom platí:
, ktorou sa potom od neho šíri vlnenie (zvuk). Ak sa toto vlnenie širi rýchlosťou c (napr. v atmosfére pri povrchu je to približne 330 m.s-1), potom platí:
 = cTZ = c/fZ. = cTZ = c/fZ. | (1) |
Z tohoto jednoduchého vzťahu vyplýva, že vlnové dĺžky bežných zvukov (okolo 1 kHz) sú rádovo metre.
Toľko na úvod, teraz už prejdem k prvému prípadu:
(i) Pohyb pozorovateľa
(a) Pohyb pozorovateľa od zdroja Táto situácia je schématicky znázornená na obrázku č. 1 vpravo. Čo som sa na ňom snažil znázorniť? Je to sekvencia troch momentov, ktoré nastali v čase t = 0, TZ a 2TZ, kde TZ je perióda kmitov zdroja. V čase t = 0 sa nachádzajú zdroj aj pozorovateľ na rovnakom mieste, pričom pozorovateľ sa pohybuje smerom doprava rýchlosťou veľkosti u (na obrázku u = c/2) a zdroj vysiela prvý signal. V následujúcom okamihu t = TZ vysiela zdroj daľší signál, zatiaľ ale pozorovateľ prešiel dráhu uTZ (na obr. cTZ/2), a tak perióda, ktorú bude prijímať pozorovateľ TP, bude vlastne čas, za ktorý k nemu dôjde druhý signál - to je 3. okamih v čase t = TP = 2TZ. To som rozoberal konkrétnu situáciu, kedy u = c/2. Pre ľubovolné u ale môžem písať: teda hľadám čas t, kedy druhý signál dorazí k pozorovateľovi, ak on prechádzal okolo zdroja práve vtedy, keď bol vyslaný prvý signál (v čase t = 0). Riešením dostanem periódu, ktorú vníma pozorovateľ: potom pre frekvenciu podľa vzťahu f = 1/T: | obrázok č. 1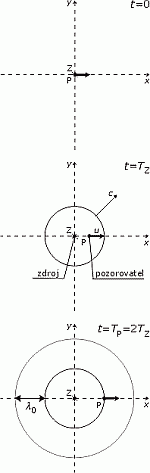
|
(b) Pohyb pozorovateľa ku zdroju Druhý možný smer pohybu pozorovateľa je smerom ku zdroju. Opäť najprv popíšem konkrétnu situáciu z obrázku č. 2 vpravo (a opäť u = c/2). Nech v čase t = 0 k pozorovateľovi práve dorazil signál a súčasne zdroj vysiela další signál. Tým, že sa pozorovateľ pohybuje smerom doľava, ide druhému signálu (vyslanému v čase t = 0) naproti a stretne sa s ním v čase t < TZ. Teda perióda kmitov pozorovateľa TP bude menšia a jeho frekvencia fP vačšia, keď sa približuje k zdroju. Aby som zistil túto pozorovateľovú periódu, hľadám vlastne čas, kedy sa stretne s druhým signálom, vyslanom v čase t = 0, kedy bol vo vzdialenosti  0 - ut = ct, 0 - ut = ct,keďže | obrázok č. 2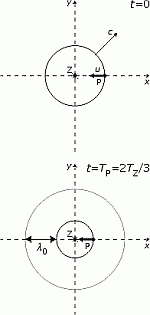
|
(ii) Pohyb zdroja
|
Na obrázku č. 3 sú dvaja pozorovatelia P1, P2 a zdroj Z, ktorý sa pohybuje smerom doprava rýchlosťou v. K pozorovateľovi P2 sa približuje a od pozorovateľa P1 sa vzďaluje. Pri pohľade na časový vývoj je vidieť, že priesečníky prvej a druhej vlnoplochy s kladnou x-ovou osou sa vzájomne pohybujú rýchlosťou c - v a priesečníky so zápornou x-ovou osou rýchlosťou c + v. To mi umožnuje zistiť vlnovú dlžku  1 = (c + v)TZ, 1 = (c + v)TZ, 2 = (c - v)TZ, 2 = (c - v)TZ,to podľa (1) pre periodu a frekvenciu pozorovateľa P1 znamená: Podobne pre pozorovateľa P2: | obrázok č. 3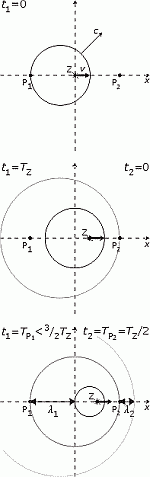
|
Zhrnutie (i) a (ii)
Predchádzajúce štyri prípady sa dajú zhrnúť do jediného vzorca, ale treba predpokladať, že zdroj zvuku bude napríklad naľavo od pozorovateľa (obrázok č. 4). Doteraz som bral rýchlosti u a v ako absolutné hodnoty, no keď zavediem ux a vx, ktoré môžu byť kladné (smer doprava) aj záporné (smer doľava), potom vo vzťažnej sústave spojenej s povrchom Zeme platí:
| fP = ((c - ux)/(c - vx))fZ |
kde fZ je pokojová frekvencia zdroja, fP je frekvencia, ktorú pozoruje (počuje) pozorovateľ pohybujúci sa rýchlosťou ux vzhľadom na prostredie, v ktorom sa šíri vlnenie (v našom prípade vzduch alebo povrch Zeme), pričom zdroj sa pohybuje rýchlosťout vx (vzhľadom na povrch Zeme). Ale pozor! Ako som už povedal, dopredu som si zvolil, že zdroj je naľavo od pozorovateľa, a tak tento vzťah treba používať. (V opačnom prípade by v ňom boli plusy.)
(iii) Všeobecný pohyb
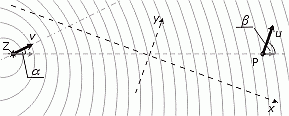
Doteraz som uvažoval pohyb zdroja a pozorovateľa, ktorý prebiehal podĺž ich spojnice a tú som položil na os x. Teraz si zvolím súradnicovú sústavu nešpeciálne a namiesto zložiek rýchlostí do smeru súradnicových osí budem používať zložky rýchlostí do spojnice ZP (a kolmice na ňu v danom bode), pričom kladný smer bude smer od zdroja k pozorovateľovi. Na obrázku č. 5 hore som zvýraznil radiálne zložky rýchlostí v smere ZP, ktoré budem značiť vr a ur. Určite platí:
 ,
,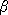 ,
,Aby som si zjednodušil ďalší postup na začiatok budem predpokladať, že pozorovateľ stojí a zdroj sa pohybuje rovnomerným pohybom, ktorý je daný ľubovolným vektorom v (obrázok č. 5 hore s tým, že zatiaľ u = 0). Neskôr budem postupne pridávať ďalšie komplikácie tak, aby som sa nakoniec dopracoval k čo najvšeobecnejšiemu pohybu. Teraz je zatiaľ nenulový iba vektor v, ktorý zviera so spojnicou zdroj-pozorovateľ (ZP) uhol  , pričom už vyriešený prípad (ii) predstavuje špeciálne riešenia pre
, pričom už vyriešený prípad (ii) predstavuje špeciálne riešenia pre  = 0 a
= 0 a  =
= 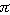 .
.
Problém však nastáva už hneď na začiatku, keď si uvedomím, že pohybom zdroja sa zároveň mení aj uhol  v čase. Tento problém sa dá vyriešiť, ale na to treba čo to zintegrovať (pozri príklad o Dopplerovom jave). Na tomto mieste si však poviem, že vzdialenosť medzi pozorovateľom a zdrojom je rádovo väčšia ako vlnová dĺžka skúmaného vlnenia. V našom prípade je tým vlnením zvuk, ktorý má vlnové dĺžky rádovo metre, takže dostanem podmienku:
v čase. Tento problém sa dá vyriešiť, ale na to treba čo to zintegrovať (pozri príklad o Dopplerovom jave). Na tomto mieste si však poviem, že vzdialenosť medzi pozorovateľom a zdrojom je rádovo väčšia ako vlnová dĺžka skúmaného vlnenia. V našom prípade je tým vlnením zvuk, ktorý má vlnové dĺžky rádovo metre, takže dostanem podmienku:
|ZP| >>  0 (~ 1 m). 0 (~ 1 m). | (2) |
|
Potom môžem uhol Chcem vlastne vedieť radiálnu vzdialenosť dvoch kružníc (vlnoplôch) rátanú v ľubovolnom smere, ktorý je daný uhlom | 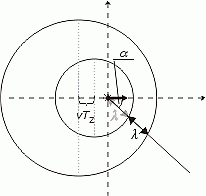 obrázok č. 6 |
ak tento vzťah prepíšem do polárnych súradníc, potom:
 cos
cos + vTZ)2 + (
+ vTZ)2 + ( sin
sin )2 = (cTZ)2,
)2 = (cTZ)2,z toho po úprave:
 = cTP = [c
= cTP = [c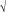 (1 - (v/c)2sin2
(1 - (v/c)2sin2 ) - vcos
) - vcos ]TZ,
]TZ,a konečne:
TP = [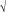 (1 - (v/c)2sin2 (1 - (v/c)2sin2 ) - (v/c)cos ) - (v/c)cos ]TZ. ]TZ. | (3) |
Ešte sa môžeš presvedčiť, že ak za  dosadíš 0 alebo
dosadíš 0 alebo 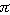 , tak dostaneš špeciálny prípad (ii).
, tak dostaneš špeciálny prípad (ii).
Teraz by som už rád do výsledku zahrnul aj pohyb pozorovateľa, no najprv zoberiem do úvahy pozorovateľa, ktorý sa pohybuje iba pozdĺž spojnice ZP. Vtedy jednoduchým zložením vzťahu (3) a analogického vzťahu pre prípad (i) dostanem:
TP = TZ[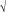 (c2 - v2sin2 (c2 - v2sin2 ) - vcos ) - vcos ]/[c - ur], ]/[c - ur], | (4) |
kde ur = +u alebo -u, podľa toho či uhol 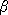 na obrázku č. 5 je 0 alebo
na obrázku č. 5 je 0 alebo 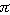 .
.
Teraz nech sa začne pozorovateľ pohybovať aj kolmo na spojnicu ZP (inými slovami uhol 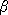 je ľubovolný), keďže platí podmienka (2), uhol
je ľubovolný), keďže platí podmienka (2), uhol  ani
ani 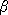 sa s časom meniť nebudú (tzn. budú sa meniť iba zanedbatelne). Z tejto podmienky však ešte vyplýva aj to, že guľové vlnenie širiace sa od zdroja môžem v okolí pozorovateľa nahradiť vlnením rovinným (pozri okolie pozorovateľa na obrázku č. 5).
sa s časom meniť nebudú (tzn. budú sa meniť iba zanedbatelne). Z tejto podmienky však ešte vyplýva aj to, že guľové vlnenie širiace sa od zdroja môžem v okolí pozorovateľa nahradiť vlnením rovinným (pozri okolie pozorovateľa na obrázku č. 5).
Ďalej, aby som sa vyhol zložitým geometrickým konštrukciám, zavediem ešte jedno podstatné zjednodušenie. Bude to podmienka, aby rýchlosť zdroja bola rádovo menšia, ako rýchlosť širenia sa vlnenia. Teda:
| v << c, | (5) |
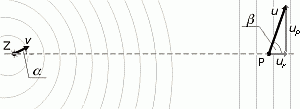
Teraz môžem v okolí pozorovateľa aproximovať guľové vlnenie od zdroja rovinným vlnením, ale kolmým na spojnicu ZP, čo vo všeobecnosti, už pri pohľade na obrázok č. 5, platiť nemusí. Čo som získal tým, že rovinným a kolmým na spojnicu ZP? Získal som to, že zmenu periódy bude spôsobovat iba radiálna zložka rýchlosti pozorovateľa a nie jeho pozdĺžna zložka rýchlosti - pozri obrázok č. 7. Použitá podmienka (5) mi ale záraveň spôsobí, ze môžem zanedbať druhý člen pod odmocninu vo vzťahu (4). Tak dostanem vzťah pre ľubovolný uhol 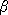 pri malých rýchlostiach zdroja:
pri malých rýchlostiach zdroja:
 )/(c - ucos
)/(c - ucos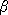 ),
),potom pre frekvencie:
fP ~ fZ(c - ucos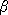 )/(c - vcos )/(c - vcos ) ) |
kde vcos , resp. ucos
, resp. ucos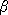 sú zložky rýchlostí zdroja, resp. pozorovateľa v smere spojnice ZP (radiálne zložky). Ešte pripomeniem, že fZ je pokojová frekvencia tónu, ktorý vydáva zdroj, fP je frekvencia, ktorú vníma pozorovateľ a c je rýchlosť zvuku.
sú zložky rýchlostí zdroja, resp. pozorovateľa v smere spojnice ZP (radiálne zložky). Ešte pripomeniem, že fZ je pokojová frekvencia tónu, ktorý vydáva zdroj, fP je frekvencia, ktorú vníma pozorovateľ a c je rýchlosť zvuku.
natT