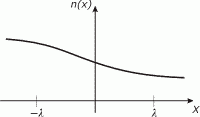

Mám nerovnováhu v koncentrácii častíc v smere osi x, napr. takú ako na obrázku hore, kde  predstavuje strednú voľnú dráhu. Vyrátam si koľko častíc mi narazí do myslenej plochy S, ktorá prechádza bodom x = 0 kolmo na os x. Zprava mi narazia všetky častice, ktoré sú bližšie ako je stredná voľná dráha
predstavuje strednú voľnú dráhu. Vyrátam si koľko častíc mi narazí do myslenej plochy S, ktorá prechádza bodom x = 0 kolmo na os x. Zprava mi narazia všetky častice, ktoré sú bližšie ako je stredná voľná dráha  . Zľava takisto. Keď to zapíšem:
. Zľava takisto. Keď to zapíšem:
 )
) S,
S, )
) S,
S,pričom 1/2 zodpovedá tomu, že v jednorozmernom priestore má vektor rýchlosti 2 možnosti smerovania.  teraz môžem prepísať pomocou strednej rýchlosti vs a času
teraz môžem prepísať pomocou strednej rýchlosti vs a času 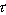 medzi dvoma zrážkami. Ďalej funkciu n(x) môžem v bodoch
medzi dvoma zrážkami. Ďalej funkciu n(x) môžem v bodoch  a -
a - aproximovať cez jej prvú deriváciu v bode 0. Dostanem tak:
aproximovať cez jej prvú deriváciu v bode 0. Dostanem tak:
 n'(0)) vs
n'(0)) vs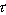 S,
S, n'(0)) vs
n'(0)) vs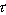 S.
S.Keď chcem teraz vypočítať koľko častíc prejde cez jednotkovú plochu v mieste x = 0 za jednotku času, musím sčítať tok zprava a zľava:
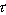 S) = -vs
S) = -vs n'(0).
n'(0).Keby boli častice nerovnomerne rozdelené aj v smere osi y alebo z, postupoval by som rovnako, aj počiatok som si mohol zvoliť kdekoľvek, a preto pre všeobecné rozdelenie častíc v priestore by mohlo platiť:
| J(x,y,z) = -D grad n(x,y,z) |
kde D - koeficient difúzie je rovný vs .
.
natT