kde
s· jednotkovΘ bßzovΘ vektory priestoru a
je Hamiltonov operßtor.Gradient je p⌠sobenie Hamiltonovho operßtora na skalßrne pole, priΦom sa vytvßra vektorovΘ pole.
1. Gradient
kde s· jednotkovΘ bßzovΘ vektory priestoru a
je Hamiltonov operßtor.
Gradient je p⌠sobenie Hamiltonovho operßtora na skalßrne pole, priΦom sa vytvßra vektorovΘ pole.
2. Divergencia
Divergencia je p⌠sobenie Hamiltonovho operßtora na vektorovΘ pole, ktorΘho v²sledkom je skalßrne pole. Divergencia je invariantnß na transformßciu s·radnφc.
3. Rotßcia
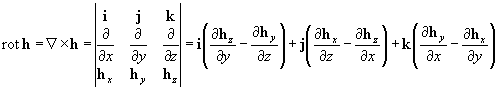
Rotßcia je p⌠sobenie Hamiltonovho operßtora na vektorovΘ pole, ktorΘho v²sledkom je vektorovΘ pole.
4. Laplaceov operßtor
Ak Laplaceov operßtor p⌠sobφ na skalßrne pole, v²sledkom je skalßrne pole.
5. d┤Allembertov operßtor
6. Zlo╛enΘ operßcie
t.j. rotßcia gradientu sa rovnß nule.
t.j. divergencia rotßcie sa rovnß nule.
t.j. rotßcia rotßcie sa rovnß gradientu divergencie mφnus Laplaceov operßtor.
7. Vety
Ak 
, potom 
takΘ, ╛e 
.
Ak 
, potom 
takΘ, ╛e 
.
E