
Na podobn² tutorißl jste u₧ jist∞ netrp∞liv∞ Φekali. NauΦφte se zßklady o detekcφch kolizφ, jak na n∞ reagovat a na fyzice zalo₧enΘ modelovacφ efekty (nßrazy, p∙sobenφ gravitace ap.). Tutorißl se vφce zam∞°uje na obecnou funkci kolizφ ne₧ zdrojov²m k≤d∙m. NicmΘn∞ d∙le₧itΘ Φßsti k≤du jsou takΘ popsßny. NeoΦekßvejte, ₧e po prvnφm p°eΦtenφ ·pln∞ vÜemu z kolizφ porozumφte. Je to komplexnφ nßm∞t, se kter²m vßm pomohu zaΦφt.
Zdrojov² k≤d, na n∞m₧ tato lekce stavφ, pochßzφ z mΘho d°φv∞jÜφho p°φsp∞vku do jednΘ sout∞₧e (najdete na OGLchallenge.dhs.org). TΘmatem byly BlßznivΘ kolize a m∙j p°φsp∞vek (mimochodem, zφskal prvnφ mφsto :-) se jmenoval Magickß mφstnost.
Detekce kolizφ jsou obtφ₧nΘ, dodnes nebylo nalezeno ₧ßdnΘ snadnΘ °eÜenφ. Samoz°ejm∞ existujφ velice obecnΘ algoritmy, kterΘ umφ pracovat s jak²mkoli druhem objekt∙, ale oΦekßvejte od nich takΘ pat°iΦnou cenu. My budeme zkoumat postupy, kterΘ jsou velmi rychlΘ, relativn∞ snadnΘ k pochopenφ a v rßmci mezφ celkem flexibilnφ. D∙raz musφ b²t vlo₧en nejen na detekci kolize, ale i na reakci objekt∙ na nßraz. Je d∙le₧itΘ, aby se vÜe d∞lo podle fyzikßlnφch zßkon∙. Mßme mnoho v∞cφ na prßci! Poj∩me se tedy podφvat, co vÜechno se v tΘto lekci nauΦφme:
T°φdy Vektor, Ray a Matrix jsou velmi u₧iteΦnΘ. Dajφ se pou₧φt v jakΘmkoli projektu. DoporuΦuji je peΦliv∞ prostudovat, t°eba se vßm budou n∞kdy hodit.
P°i detekci kolizφ vyu₧ijeme algoritmus, kter² se v∞tÜinou pou₧φvß v trasovßnφ polop°φmek (ray tracing). Vektorovß reprezentace polop°φmky je tvo°ena bodem, kter² oznaΦuje zaΦßtek a vektorem (obyΦejn∞ normalizovan²m) urΦujφcφm sm∞r polop°φmky. Rovnice polop°φmky:
bod_na_polop°φmce = zaΦßtek + t * sm∞r
╚φslo t nab²vß hodnot od nuly do nekoneΦna. Dosadφme-li nulu zφskßme poΦßteΦnφ bod. U v∞tÜφch Φφsel dostaneme odpovφdajφcφ body na polop°φmce. Bod, poΦßtek i sm∞r jsou 3D vektory se slo₧kami x, y, a z. Nynφ m∙₧eme pou₧φt tuto reprezentaci polop°φmky k v²poΦtu pr∙seΦφku s rovinou nebo vßlcem.
Vektorovß reprezentace roviny vypadß takto:
Xn dot X = d
Xn je normßla roviny, X je bod na jejφm povrchu a d je Φφslo, kterΘ urΦuje vzdßlenost roviny od poΦßtku sou°adnicovΘho systΘmu.
P°ekl.: Pod operacφ "dot" se skr²vß skalßrnφ souΦin dvou vektor∙ (dot product), kter² se vypoΦte souΦtem nßsobk∙ jednotliv²ch x, y a z slo₧ek. Nechßvßm ho v p∙vodnφm zn∞nφ, proto₧e i ve zdrojov²ch k≤dech budeme volat metodu dot().
P°ekl.: P dot Q = Px * Qx + Py * Qy + Pz * Qz
Abychom definovali rovinu, pot°ebujeme 3D bod a vektor, kter² je kolm² k rovin∞. Pokud vezmeme za 3D bod vektor (0, 0, 0) a pro normßlu vektor (0, 1, 0), protφnß rovina osy x a z. Pokud znßme bod a normßlu, dß se chyb∞jφcφ Φφslo d snadno dopoΦφtat.
Pozn.: Vektorovß reprezentace roviny je ekvivalentnφ vφce znßmΘ form∞ Ax + By + Cz + D = 0 (obecnß rovnice roviny). Pro p°epoΦet dosa∩te za A, B, C slo₧ky normßly a p°i°a∩te D = -d.
Nynφ mßme dv∞ rovnice
bod_na_polop°φmce = zaΦßtek + t * sm∞r
Xn dot X = d
Pokud polop°φmka protne rovinu v n∞jakΘm bod∞, musφ sou°adnice pr∙seΦφk∙ vyhovovat ob∞ma rovnicφm
Xn dot bod_na_polop°φmce = d
Nebo
(Xn dot zaΦßtek) + t * (Xn dot sm∞r) = d
Vyjßd°φme t
t = (d - Xn dot zaΦßtek) / (Xn dot sm∞r)
Dosadφme d
t = (Xn dot bod_na_polop°φmce - Xn dot zaΦßtek) / (Xn dot sm∞r)
Vytkneme Xn
t = (Xn dot (bod_na_polop°φmce - zaΦßtek)) / (Xn dot sm∞r)
╚φslo t reprezentuje vzdßlenost od zaΦßtku polop°φmky k pr∙seΦφku s rovinou ve sm∞ru polop°φmky (ne na kolmici). Dosazenφm t do rovnice polop°φmky zφskßme koliznφ bod. Existuje n∞kolik specißlnφch situacφ. Pokud Xn dot sm∞r = 0, budou tyto dva vektory navzßjem kolmΘ. Polop°φmka prochßzφ rovnob∞₧n∞ s rovinou a tudφ₧ neexistuje koliznφ bod. Pokud je t zßpornΘ, pr∙seΦφk le₧φ p°ed poΦßteΦnφm bodem. Polop°φmka nesm∞°uje k rovin∞, ale od nφ. Op∞t ₧ßdn² pr∙seΦφk.
int TestIntersionPlane(const Plane& plane, const TVector& position, const TVector& direction, double& lamda, TVector& pNormal)
{
double DotProduct = direction.dot(plane._Normal);// Skalßrnφ souΦin vektor∙
double l2;// UrΦuje koliznφ bod
if ((DotProduct < ZERO) && (DotProduct > -ZERO))// Je polop°φmka rovnob∞₧nß s rovinou?
return 0;// Bez pr∙seΦφku
l2 = (plane._Normal.dot(plane._Position - position)) / DotProduct;// Dosazenφ do vzorce
if (l2 < -ZERO)// Sm∞°uje polop°φmka od roviny?
return 0;// Bez pr∙seΦφku
pNormal = plane._Normal;// Normßla roviny
lamda = l2;// Koliznφ bod
return 1;// Pr∙seΦφk existuje
}
V²poΦet pr∙seΦφku polop°φmky s nekoneΦn∞ dlouh²m vßlcem je mnohem komplikovan∞jÜφ ne₧ vysv∞tlenφ toho, proΦ se tφm zde nebudeme zab²vat. Na pozadφ je p°φliÜ mnoho matematiky. M²m primßrnφm zßm∞rem je poskytnout a vysv∞tlit nßstroje bez zabφhßnφ do zbyteΦn²ch detail∙, kterΘ by stejn∞ n∞kte°φ nepochopili. Vßlec je tvo°en polop°φmkou, kterß reprezentuje jeho osu, a polom∞rem podstavy. Pro detekci kolize se v tomto tutorißlu pou₧φvß funkce TestIntersetionCylinder(), kterß vracφ jedniΦku, pokud byl nalezen pr∙seΦφk, jinak nulu.
int TestIntersionCylinder(const Cylinder& cylinder, const TVector& position, const TVector& direction, double& lamda, TVector& pNormal, TVector& newposition)
V parametrech se p°edßvß struktura vßlce, zaΦßtek a sm∞rov² vektor polop°φmky. Krom∞ nßvratovΘ hodnoty zφskßme z funkce vzdßlenost od pr∙seΦφku (na polop°φmce), normßlu vychßzejφcφ z pr∙seΦφku a bod pr∙seΦφku.
Koule je v geometrii reprezentovßna st°edem a polom∞rem. ZjiÜt∞nφ, jestli do sebe dv∞ koule narazily je banßlnφ. VypoΦteme vzdßlenost mezi dv∞ma st°edy a porovnßme ji se souΦtem polom∞r∙. Jak snadnΘ!
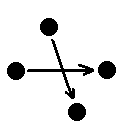
ProblΘmy nastanou p°i hledßnφ koliznφho bodu dvou POHYBUJ═C═CH se koulφ. Na obrßzku je p°φklad, kdy se dv∞ koule p°esunou z jednoho mφsta do druhΘho za urΦit² Φasov² ·sek. Jejich drßhy se protφnajφ, ale to nenφ dostateΦn² d∙vod k tvrzenφ, ₧e do sebe opravdu narazφ. Mohou se nap°φklad pohybovat rozdφlnou rychlostφ. Jedna tΘm∞° stojφ a druhß je za okam₧ik ·pln∞ n∞kde jinde.

V p°edchozφch metodßch jsme °eÜili rovnice dvou geometrick²ch objekt∙. Pokud podobnß rovnice pro dan² objekt neexistuje nebo nem∙₧e b²t pou₧ita (pohyb po slo₧itΘ k°ivce), pou₧φvß se jinß metoda. V naÜem p°φpad∞ znßme poΦßteΦnφ i koncovΘ body p°esunu, Φasov² krok, rychlost (+sm∞r) a metodu zjiÜt∞nφ nßrazu statick²ch koulφ. Rozkouskujeme Φasov² ·sek na malΘ Φßsti. Koule budeme v zßvislosti na nich postupn∞ posunovat a poka₧dΘ testovat kolizi. Pokud najdeme n∞kter² bod, kdy je vzdßlenost koulφ menÜφ ne₧ souΦet jejich polom∞r∙, vezmeme minulou pozici a oznaΦφme ji jako koliznφ bod. M∙₧e se jeÜt∞ zaΦφt interpolovat mezi t∞mito dv∞ma body na rozhranφ, kdy kolize jeÜt∞ nebyla a u₧ je, abychom naÜli ·pln∞ p°esnou pozici, ale v∞tÜinou to nenφ pot°eba.
╚φm menÜφ bude Φasov² ·sek, tφm budou Φßsti vzniklΘ rozsekßnφm menÜφ a metoda bude vφce p°esnß (a vφce nßroΦnß na hardware poΦφtaΦe). Nap°φklad, pokud bude Φasov² ·sek 1 a Φßsti 3, budeme zjiÜ¥ovat kolizi v Φasech 0, 0,33, 0,66 a 1. V nßsledujφcφm v²pisu k≤du hledßme koule, kterΘ b∞hem nßsledujφcφho ΦasovΘho kroku narazφ do kterΘkoli z ostatnφch. Funkce vrßtφ indexy obou koulφ, bod a Φas nßrazu.
int FindBallCol(TVector& point, double& TimePoint, double Time2, int& BallNr1, int& BallNr2)
{
TVector RelativeV;// Relativnφ rychlost mezi koulemi
TRay rays;// Polop°φmka
double MyTime = 0.0;// Hledßnφ p°esnΘ pozice nßrazu
double Add = Time2 / 150.0;// Rozkouskuje Φasov² ·sek na 150 Φßstφ
double Timedummy = 10000;// ╚as nßrazu
TVector posi;// Pozice na polop°φmce
// Test vÜech koulφ proti vÜem ostatnφm po 150 krocφch
for (int i = 0; i < NrOfBalls - 1; i++)// VÜechny koule
{
for (int j = i + 1; j < NrOfBalls; j++)// VÜechny zb²vajφcφ koule
{
// V²poΦet vzdßlenosti
RelativeV = ArrayVel[i] - ArrayVel[j];// Relativnφ rychlost mezi koulemi
rays = TRay(OldPos[i], TVector::unit(RelativeV));// Polop°φmka
if ((rays.dist(OldPos[j])) > 40)// Je vzdßlenost v∞tÜφ ne₧ 2 polom∞ry?
{
continue;// DalÜφ
}
// Nßraz
MyTime = 0.0;// Inicializace p°ed vstupem do cyklu
while (MyTime < Time2)// P°esn² bod nßrazu
{
MyTime += Add;// Zv∞tÜφ Φas
posi = OldPos[i] + RelativeV * MyTime;//P°esun na dalÜφ bod (pohyb na polop°φmce)
if (posi.dist(OldPos[j]) <= 40)// Nßraz
{
point = posi;// Bod nßrazu
if (Timedummy > (MyTime - Add))// Bli₧Üφ nßraz, ne₧ kter² jsme u₧ naÜli (v Φase)?
{
Timedummy = MyTime - Add;// P°i°adit Φas nßrazu
}
BallNr1 = i;// OznaΦenφ koulφ, kterΘ narazily
BallNr2 = j;
break;// UkonΦφ vnit°nφ cyklus
}
}
}
}
if (Timedummy != 10000)// NaÜli jsme kolizi?
{
TimePoint = Timedummy;// ╚as nßrazu
return 1;// ┌sp∞ch
}
return 0;// Bez kolize
}
Nynφ u₧ umφme zjistit pr∙seΦφk polop°φmky a roviny/vßlce. Tyto znalosti pou₧ijeme pro hledßnφ kolizφ mezi koulφ a jednφm z t∞chto objekt∙. Pot°ebujeme najφt p°esn² bod nßrazu. P°evod znalostφ z polop°φmky na pohybujφcφ se kouli je relativn∞ snadn². Podφvejte se na lev² obrßzek, mo₧nß, ₧e podstatu pochopφte sami.
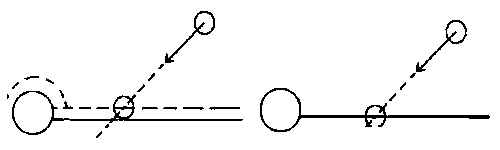
Ka₧dß koule sice mß polom∞r, ale my ji budeme brßt jako bezrozm∞rnou Φßsti, kterß mß pouze pozici. K povrchu t∞lesa p°iΦteme ve sm∞ru normßlovΘho vektoru offset urΦen² polom∞rem koule. Neboli k polom∞ru vßlce p°iΦteme pr∙m∞r koule (2 polom∞ry; z ka₧dΘ strany jeden). Operacφ jsme se vrßtili k detekci kolize polop°φmka - vßlec. Rovina je jeÜt∞ jednoduÜÜφ. Posuneme ji sm∞rem ke kouli o jejφ polom∞r. Na obrßzku jsou Φßrkovan∞ nakresleny "virtußlnφ" objekty pro testy kolizφ a pln∞ objekty, kterΘ program vykreslφ. Kdybychom k objekt∙m p°i testech nep°ipoΦφtßvali offset, koule by p°ed odrazem z poloviny pronikaly do objekt∙ (obrßzek vpravo).
Mßme-li urΦit mφsto nßrazu, je vhodnΘ nejd°φve zjistit, jestli kolize nastane p°i aktußlnφm ΦasovΘm ·seku. Proto₧e polop°φmka mß nekoneΦnou dΘlku, je v₧dy mo₧nΘ, ₧e se koliznφ bod nachßzφ a₧ n∞kde za novou pozicφ koule. Abychom to zjistili, spoΦφtßme novou pozici a urΦφme vzdßlenost mezi poΦßteΦnφm a koncov²m bodem. Pokud je tato vzdßlenost kratÜφ ne₧ vzdßlenost, o kterou se objekt posune, tak mßme jistotu, ₧e kolize nastane v tomto ΦasovΘm ·seku. Abychom spoΦφtali p°esn² Φas kolize pou₧ijeme nßsledujφcφ jednoduchou rovnici. Dst p°edstavuje vzdßlenost mezi poΦßteΦnφm a koncov²m bodem, Dsc vzdßlenost mezi poΦßteΦnφm a koliznφm bodem a Φasov² krok je definovßn jako T. ╪eÜenφm zφskßme Φas kolize Tc.
Tc = Dsc * T / Dst
V²poΦet se provede samoz°ejm∞ jenom tehdy, kdy₧ mß kolize nastat v tomto ΦasovΘm kroku. Vrßcen² Φas je zlomkem (Φßstφ) celΘho ΦasovΘho kroku. Pokud bude Φasov² krok 1 s a my nalezneme koliznφ bod p°esn∞ uprost°ed vzdßlenosti, Φas kolize se bude rovnat 0,5 s. Je interpretovßn jako: V ΦasovΘm okam₧iku 0,5 sekund po zaΦßtku p°esunu do sebe objekty narazφ. Koliznφ bod se vypoΦte nßsobenφm Φasu Tc aktußlnφ rychlostφ a p°iΦtenφm poΦßteΦnφho bodu.
bod_kolize = start + rychlost * Tc
Tento koliznφ bod je vÜak na objektu s offsetem (pomocnΘm). Abychom nalezli bod nßrazu na reßlnΘm objektu, p°iΦteme k bodu kolize invertovan² normßlov² vektor z bodu kolize, kter² mß velikost polom∞ru koule. Normßlov² vektor zφskßme z funkce pro kolize. VÜimn∞te si, ₧e funkce pro kolizi s vßlcem vracφ bod nßrazu, tak₧e nemusφ b²t znovu poΦφtßn.
OÜet°enφ toho, jak se koule zachovß po nßrazu je stejn∞ d∙le₧itΘ jako samotnΘ nalezenφ koliznφho bodu. Pou₧itΘ algoritmy a funkce popisujφ p°esn² bod nßrazu, normßlov² vektor vychßzejφcφ z objekt∙ v mφst∞ nßrazu a Φasov² ·sek, ve kterΘm kolize nastala.
P°i odrazech nßm pomohou fyzikßlnφ zßkony. Implementujeme pouΦku: "┌hel dopadu se rovnß ·hlu odrazu". Oba ·hly se vztahujφ k normßlovΘmu vektoru, kter² vychßzφ z objektu v koliznφm bod∞. Nßsledujφcφ obrßzek ukazuje odraz polop°φmky od koule.
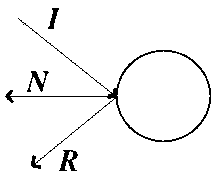
I je sm∞rov² vektor p°ed nßrazem, N je normßlov² vektor v bod∞ kolize a R je sm∞rov² vektor po odrazu, kter² se vypoΦte podle nßsledujφcφ rovnice:
R = 2 * (-I dot N) * N + I
Omezenφ spoΦφvß v tom, ₧e I i N musφ b²t jednotkovΘ vektory. U nßs vÜak dΘlka vektoru reprezentuje rychlost a sm∞r koule, a proto nem∙₧e b²t bez transformace dosazen do rovnice. Pot°ebujeme z n∞j vyjmout rychlost. Nalezneme jeho velikost a vyd∞lφme jφ jednotlivΘ x, y, z slo₧ky. Zφskan² jednotkov² vektor dosadφme do rovnice a vypoΦteme R. Jsme skoro u konce. Vektor nynφ mφ°φ ve sm∞ru odra₧enΘ polop°φmky, ale nemß p∙vodnφ dΘlku. Minule jsme d∞lili, tak₧e te∩ budeme nßsobit.
Nßsledujφcφ v²pis k≤du se pou₧φvß pro v²poΦet odrazu po kolizi koule s rovinou nebo vßlcem. Uveden² algoritmus pracuje i s jin²mi povrchy, nezßle₧φ na jejich tvaru. Pokud nalezneme bod kolize a normßlu, je odraz v₧dy stejn².
rt2 = ArrayVel[BallNr].mag();// Ulo₧φ dΘlku vektoru
ArrayVel[BallNr].unit();// Normalizace vektoru
// V²poΦet odrazu
ArrayVel[BallNr] = TVector::unit((normal * (2 * normal.dot(-ArrayVel[BallNr]))) + ArrayVel[BallNr]);
ArrayVel[BallNr] = ArrayVel[BallNr] * rt2;// Nastavenφ p∙vodnφ dΘlky
OÜet°enφ vzßjemnΘho nßrazu dvou pohybujφcφch se koulφ je mnohem obtφ₧n∞jÜφ. Musφ b²t vy°eÜeny slo₧itΘ rovnice. Nebudeme nic odvozovat, pouze vysv∞tlφm v²sledek. Situace p°i kolizi dvou koulφ vypadß p°ibli₧n∞ takto:
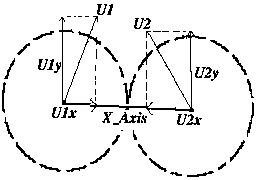
Vektory U1 a U2 p°edstavujφ rychlost koulφ v Φase nßrazu. St°edy dohromady spojuje osa X_Axis, na kterΘ le₧φ vektory U1x a U2x, co₧ jsou vlastn∞ pr∙m∞ty rychlosti. U1y a U2y jsou projekce rychlosti na osu, kterß je kolmß k X_Axis. K jejich v²poΦtu postaΦφ jednoduch² skalßrnφ souΦin.
Do nßsledujφcφch rovnic dosazujeme jeÜt∞ Φφsla M1 a M2, kterß vyjad°ujφ hmotnost koulφ. Sna₧φme se vypoΦφtat orientaci vektor∙ rychlosti U1 a U2 po odrazu. Budou je vyjad°ovat novΘ vektory V1 a V2. ╚φsla V1x, V1y, V2x, V2y jsou op∞t pr∙m∞ty.
a) najφt X_Axis
X_Axis = (st°ed2 - st°ed1)
Jednotkov² vektor, X_Axis.unit();
b) najφt projekce
U1x = X_Axis * (X_Axis dot U1)
U1y = U1 - U1x
U2x = -X_Axis * (-X_Axis dot U2)
U2y = U2 - U2x
c) najφt novΘ rychlosti
V1x = ((U1x * M1) + (U2x * M2) - (U1x - U2x) * M2) / (M1 + M2)
V2x = ((U1x * M1) + (U2x * M2) - (U2x - U1x) * M1) / (M1 + M2)
V naÜφ aplikaci nastavujeme jednotkovou hmotnost (M1 = M2 = 1), a proto se v²poΦet v²sledn²ch vektor∙ velmi zjednoduÜφ.
d) najφt koneΦnΘ rychlosti
V1y = U1y
V2y = U2y
V1 = V1x + V1y
V2 = V2x + V2y
Odvozenφ rovnic stßlo hodn∞ prßce, ale jakmile se nachßzejφ v tΘto form∞, je jejich pou₧itφ docela snadnΘ. K≤d, kterΘ vykonßvß srß₧ky dvou koulφ vypadß takto:
TVector pb1, pb2, xaxis, U1x, U1y, U2x, U2y, V1x, V1y, V2x, V2y;// Deklarace prom∞nn²ch
double a, b;
pb1 = OldPos[BallColNr1] + ArrayVel[BallColNr1] * BallTime;// Nalezenφ pozice koule 1
pb2 = OldPos[BallColNr2] + ArrayVel[BallColNr2] * BallTime;// Nalezenφ pozice koule 2
xaxis = (pb2 - pb1).unit();// Nalezenφ X_Axis
a = xaxis.dot(ArrayVel[BallColNr1]);// Nalezenφ projekce
U1x = xaxis * a;// Nalezenφ pr∙m∞t∙ vektor∙
U1y = ArrayVel[BallColNr1] - U1x;
xaxis = (pb1 - pb2).unit();
b = xaxis.dot(ArrayVel[BallColNr2]);// To samΘ pro druhou kouli
U2x = xaxis * b;
U2y = ArrayVel[BallColNr2] - U2x;
V1x = (U1x + U2x - (U1x - U2x)) * 0.5;// Nalezenφ nov²ch rychlostφ
V2x = (U1x + U2x - (U2x - U1x)) * 0.5;
V1y = U1y;
V2y = U2y;
for (j = 0; j < NrOfBalls; j++)// Posun vÜech koulφ do Φasu nßrazu
{
ArrayPos[j] = OldPos[j] + ArrayVel[j] * BallTime;
}
ArrayVel[BallColNr1] = V1x + V1y;// Nastavenφ prßv∞ vypoΦφtan²ch vektor∙ koulφm, kterΘ do sebe narazily
ArrayVel[BallColNr2] = V2x + V2y;
Pro simulaci realistick²ch pohyb∙ nejsou nßrazy, hledßnφ koliznφch bod∙ a odrazy dostateΦnΘ. Musφ b²t p°idßn jeÜt∞ pohyb podle fyzikßlnφch zßkon∙. Asi nejpou₧φvan∞jÜφ metodou jsou Eulerovy rovnice. VÜechny v²poΦty se vykonßvajφ pro urΦit² Φasov² ·sek. To znamenß, ₧e se celß simulace neposouvß vp°ed plynule, ale po urΦit²ch skocφch. P°edstavte si, ₧e mßte fotoaparßt a ka₧dou vte°inu v²slednou scΘnu vyfotφte. B∞hem tΘto vte°iny se provedou vÜechny pohyby, testy kolizφ a odrazy. V²sledn² obrßzek se zobrazφ na monitoru a z∙stane tam a₧ do dalÜφ vte°iny. Op∞t stejnΘ v²poΦty a dalÜφ zobrazenφ. Takto pracujφ vÜechny poΦφtaΦovΘ animace, ale mnohem rychleji. Oko, stejn∞ jako u filmu, vidφ plynul² pohyb. V zßvislosti na Eulerov²ch rovnicφch se rychlost a pozice v ka₧dΘm ΦasovΘm kroku zm∞nφ takto:
novß_rychlost = starß_rychlost + zrychlenφ * Φasov² ·sek
novß_pozice = starß_pozice + novß_rychlost * Φasov² ·sek
Nynφ se objekty pohybujφ a testujφ na kolize s pou₧itφm novΘ rychlosti. Zrychlenφ objektu je zφskßno vyd∞lenφm sφly, kterß na n∞j p∙sobφ, jeho hmotnostφ.
zrychlenφ = sφla / hmotnost
V tomto demu je gravitace jedinß sφla, kterß p∙sobφ na objekt. M∙₧e b²t reprezentovßna vektorem, kter² udßvß gravitaΦnφ zrychlenφ. U nßs se bude tento vektor rovnat (0; -0,5; 0). To znamenß, ₧e na zaΦßtku ka₧dΘho ΦasovΘho ·seku spoΦφtßme novou rychlost koule a s testovßnφm kolizφ ji posuneme. Pokud b∞hem ΦasovΘho ·seku narazφ (nap°. po 0,5 s), posuneme ji na pozici kolize, vypoΦteme odraz (nov² vektor rychlosti) a p°esuneme ji o zb²vajφcφ Φas (0,5 s). V n∞m op∞t testujeme kolize atd. Opakujeme tak dlouho, dokud zb²vß n∞jak² Φas.
Pokud je p°φtomno vφce pohybujφcφch se objekt∙, musφ b²t nejprve testovßn ka₧d² z nich na nßrazy do statick²ch objekt∙. Ulo₧φ se Φasov∞ nejbli₧Üφ z nich. Potom se provedou testy nßraz∙ mezi pohybujφcφmi se objekty - ka₧d² s ka₧d²m. Vrßcen² Φas je porovnßn s Φasem u test∙ se statick²mi objekty a v ·vahu je brßn nejbli₧Üφ nßraz. Celß simulace se posune do tohoto Φasu. VypoΦte se odraz objektu a op∞t se provedou detekce nßraz∙ do statick²ch objekt∙ atd. atd. atd. - dokud zb²vß n∞jak² Φas. P°ekreslφ se scΘna a vÜe se opakuje nanovo.
Kdykoli, kdy₧ se objekty srazφ, nastane exploze, kterß se zobrazφ na sou°adnicφch pr∙seΦφku. Velmi jednoduchou cestou je alfablending dvou polygon∙, kterΘ jsou navzßjem kolmΘ a jejich st°ed je na sou°adnicφch koliznφho bodu. Oba polygony se postupn∞ zv∞tÜujφ a zpr∙hled≥ujφ. Alfa hodnota se zmenÜuje z poΦßteΦnφ jedniΦky a₧ na nulu. Dφky Z bufferu m∙₧e spousta alfablendovan²ch polygon∙ zp∙sobovat problΘmy - navzßjem se p°ekr²vajφ, a proto si p∙jΦφme techniku pou₧φvanou p°i renderingu Φßstic. Abychom vÜe d∞lali sprßvn∞, musφme polygony °adit od zadnφch po p°ednφ podle vzdßlenosti od pozorovatele. TakΘ vypneme zßpis do Depth bufferu (ne Φtenφ). VÜimn∞te si, ₧e omezujeme poΦet explozφ na maximßln∞ dvacet na jeden snφmek. Nastane-li jich najednou vφce, pole se zaplnφ a dalÜφ se nebudou brßt v ·vahu. Nßsleduje k≤d, kter² aktualizuje a renderuje exploze.
glEnable(GL_BLEND);// Blending
glDepthMask(GL_FALSE);// Vypne zßpis do depth bufferu
glBindTexture(GL_TEXTURE_2D, texture[1]);// Textura exploze
for(i = 0; i < 20; i++)// Prochßzφ v²buchy
{
if(ExplosionArray[i]._Alpha >= 0)// Je exploze vid∞t?
{
glPushMatrix();// Zßloha matice
ExplosionArray[i]._Alpha -= 0.01f;// Aktualizace alfa hodnoty
ExplosionArray[i]._Scale += 0.03f;// Aktualizace m∞°φtka
glColor4f(1, 1, 0, ExplosionArray[i]._Alpha);// Älutß barva s pr∙hlednostφ
glScalef(ExplosionArray[i]._Scale, ExplosionArray[i]._Scale, ExplosionArray[i]._Scale);// Zm∞na m∞°φtka
glTranslatef((float)ExplosionArray[i]._Position.X() / ExplosionArray[i]._Scale, (float)ExplosionArray[i]._Position.Y() / explosionArray[i]._Scale, (float)ExplosionArray[i]._Position.Z() / ExplosionArray[i]._Scale);// P°esun na pozici koliznφho bodu, m∞°φtko je offsetem
glCallList(dlist);// Zavolß display list
glPopMatrix();// Obnova p∙vodnφ matice
}
}
glDepthMask(GL_TRUE);// Obnova p∙vodnφch parametr∙ OpenGL
glDisable(GL_BLEND);
glDisable(GL_TEXTURE_2D);
Pro p°ehrßvßnφ zvuk∙ se pou₧φvß funkce PlaySound() z multimedißlnφ knihovny Windows - rychlß cesta, jak bez problΘm∙ p°ehrßt .wav zvuk.
Gratuluji... pokud stßle Φtete, ·sp∞Ün∞ jste se prokousali dlouhou a nßroΦnou teoretickou sekcφ. P°edtφm, ne₧ si zaΦnete hrßt s demem, m∞l by b²t jeÜt∞ vysv∞tlen zdrojov² k≤d. Ze vÜeho nejd°φve se ale p∙jdeme podφvat na globßlnφ prom∞nnΘ.
Vektory dir a pos reprezentujφ pozici a sm∞r kamery, kterou v programu pohybujeme funkcφ gluLookAt(). Pokud scΘna nenφ vykreslovßna v m≤du "sledovßnφ koule", otßΦφ se kolem osy y.
TVector dir;// Sm∞r kamery
TVector pos(0, -50, 1000);// Pozice kamery
float camera_rotation = 0;// Rotace scΘny na ose y
Gravitace, kterß p∙sobφ na koule.
TVector accel(0, -0.05, 0);// GravitaΦnφ zrychlenφ aplikovanΘ na koule
Pole, kterß uklßdajφ novou a starou pozici vÜech koulφ a jejich sm∞r. PoΦet koulφ je natvrdo nastaven na deset.
TVector ArrayVel[10];// Rychlost koulφ
TVector ArrayPos[10];// Pozice koulφ
TVector OldPos[10];// StarΘ pozice koulφ
╚asov² ·sek pro simulaci.
double Time = 0.6;// ╚asov² krok simulace
Pokud je tato prom∞nnß v jedniΦce, zm∞nφ se m≤d kamery tak, aby sledovala pohyby koule. Pro jejφ umφst∞nφ a nasm∞rovßnφ se pou₧ije pozice a sm∞r koule s indexem 1, kterß tedy bude v₧dy v zßb∞ru.
int hook_toball1 = 0;// Sledovat kamerou kouli?
Nßsledujφcφ struktury se popisujφ samy sv²m jmΘnem. Budou uklßdat data o rovinßch, vßlcφch a explozφch.
struct Plane// Struktura roviny
{
TVector _Position;
TVector _Normal;
};
struct Cylinder// Struktura vßlce
{
TVector _Position;
TVector _Axis;
double _Radius;
};
struct Explosion// Struktura exploze
{
TVector _Position;
float _Alpha;
float _Scale;
};
Objekty struktur.
Plane pl1, pl2, pl3, pl4, pl5;// P∞t rovin mφstnosti (bez stropu)
Cylinder cyl1, cyl2, cyl3;// T°i vßlce
Explosion ExplosionArray[20];// Dvacet explozφ
Textury, display list, quadratic.
GLuint texture[4];// ╚ty°i textury
GLuint dlist;// Display list v²buchu
GLUquadricObj *cylinder_obj;// Quadratic pro kreslenφ koulφ a vßlc∙
Funkce pro kolize koulφ se statick²mi objekty a mezi koulemi navzßjem.
int TestIntersionPlane(const Plane& plane, const TVector& position, const TVector& direction, double& lamda, TVector& pNormal);
int TestIntersionCylinder(const Cylinder& cylinder, const TVector& position, const TVector& direction, double& lamda, TVector& pNormal, TVector& newposition);
int FindBallCol(TVector& point, double& TimePoint, double Time2, int& BallNr1, int& BallNr2);
Loading textur, inicializace prom∞nn²ch, logika simulace, renderovßnφ scΘny a inicializace OpenGL.
void LoadGLTextures();
void InitVars();
void idle();
int DrawGLScene(GLvoid);
int InitGL(GLvoid)
Pro informace o geometrick²ch t°φdßch vektoru, polop°φmky a matice nahlΘdn∞te do zdrojov²ch k≤d∙. Jsou velmi u₧iteΦnΘ a mohou b²t bez problΘm∙ vyu₧ity ve vaÜich vlastnφch programech.
Nejd∙le₧it∞jÜφ kroky simulace nejprve popφÜi pseudok≤dem.
while (Φasov² ·sek != 0)
{
for (ka₧dß koule)
{
V²poΦet nejbli₧Üφ kolize s rovinami;
V²poΦet nejbli₧Üφ kolize s vßlci;
Ulo₧it/nahradit "zßznam" o kolizi, pokud je to do te∩ nejbli₧Üφ kolize v Φase;
}
Testy kolizφ mezi pohybujφcφmi se koulemi;
Ulo₧it/nahradit "zßznam" o kolizi, pokud je to do te∩ nejbli₧Üφ kolize v Φase;
if (nastala kolize?)
{
P°esun vÜech koulφ do Φasu nejbli₧Üφ kolize;
(U₧ mßme vypoΦten bod, normßlu a Φas kolize.)
V²poΦet odrazu;
Φasov² ·sek -= Φas kolize;
}
else
{
P°esun vÜech koulφ na konec ΦasovΘho ·seku;
}
}
Zdrojov² k≤d zalo₧en² na pseudok≤du je na prvnφ pohled mnohem vφce nßroΦn² na Φtenφ a hlavn∞ pochopenφ, nicmΘn∞ v zßkladu je jeho p°esnou implementacφ.
void idle()// SimulaΦnφ logika - kolize
{
// Deklarace prom∞nn²ch
double rt, rt2, rt4, lamda = 10000;
TVector norm, uveloc;
TVector normal, point, time;
double RestTime, BallTime;
TVector Pos2;
int BallNr = 0, dummy = 0, BallColNr1, BallColNr2;
TVector Nc;
if (!hook_toball1)// Pokud kamera nesleduje kouli
{
camera_rotation += 0.1f;// PootoΦenφ scΘny
if (camera_rotation > 360)// OÜet°enφ p°eteΦenφ
{
camera_rotation = 0;
}
}
RestTime = Time;
lamda = 1000;
// V²poΦet rychlostφ vÜech koulφ pro nßsledujφcφ Φasov² ·sek (Eulerovy rovnice)
for (int j = 0; j < NrOfBalls; j++)
{
ArrayVel[j] += accel * RestTime;
}
while (RestTime > ZERO)// Dokud neskonΦil Φasov² ·sek
{
lamda = 10000;// Inicializace na velmi vysokou hodnotu
// Kolize vÜech koulφ s rovinami a vßlci
for (int i = 0; i < NrOfBalls; i++)// VÜechny koule
{
// V²poΦet novΘ pozice a vzdßlenosti
OldPos[i] = ArrayPos[i];
TVector::unit(ArrayVel[i], uveloc);
ArrayPos[i] = ArrayPos[i] + ArrayVel[i] * RestTime;
rt2 = OldPos[i].dist(ArrayPos[i]);
// Kolize koule s rovinou
if (TestIntersionPlane(pl1, OldPos[i], uveloc, rt, norm))
{
// ╚as nßrazu
rt4 = rt * RestTime / rt2;
// Pokud je menÜφ ne₧ n∞kter² z d°φve nalezen²ch nahradit ho
if (rt4 <= lamda)
{
if (rt4 <= RestTime + ZERO)
{
if (!((rt <= ZERO) && (uveloc.dot(norm) > ZERO)))
{
normal = norm;
point = OldPos[i] + uveloc * rt;
lamda = rt4;
BallNr = i;
}
}
}
}
if (TestIntersionPlane(pl2, OldPos[i], uveloc, rt, norm))
{
// To samΘ jako minule, ale s jinou rovinou
}
if (TestIntersionPlane(pl3, OldPos[i], uveloc, rt, norm))
{
// To samΘ jako minule, ale s jinou rovinou
}
if (TestIntersionPlane(pl4, OldPos[i], uveloc, rt, norm))
{
// To samΘ jako minule, ale s jinou rovinou
}
if (TestIntersionPlane(pl5, OldPos[i], uveloc, rt, norm))
{
// To samΘ jako minule, ale s jinou rovinou
}
// Kolize koule s vßlcem
if (TestIntersionCylinder(cyl1, OldPos[i], uveloc, rt, norm, Nc))
{
rt4 = rt * RestTime / rt2;
if (rt4 <= lamda)
{
if (rt4 <= RestTime + ZERO)
{
if (!((rt <= ZERO) && (uveloc.dot(norm) > ZERO)))
{
normal = norm;
point = Nc;
lamda = rt4;
BallNr = i;
}
}
}
}
if (TestIntersionCylinder(cyl2, OldPos[i], uveloc, rt, norm, Nc))
{
// To samΘ jako minule, ale s jin²m vßlcem
}
if (TestIntersionCylinder(cyl3, OldPos[i], uveloc, rt, norm, Nc))
{
// To samΘ jako minule, ale s jin²m vßlcem
}
}
// Kolize mezi koulemi
if (FindBallCol(Pos2, BallTime, RestTime, BallColNr1, BallColNr2))
{
if (sounds)// Jsou zapnutΘ zvuky?
{
PlaySound("Data/Explode.wav", NULL, SND_FILENAME | SND_ASYNC);
}
if ((lamda == 10000) || (lamda > BallTime))
{
RestTime = RestTime - BallTime;
TVector pb1, pb2, xaxis, U1x, U1y, U2x, U2y, V1x, V1y, V2x, V2y;// Deklarace prom∞nn²ch
double a, b;
pb1 = OldPos[BallColNr1] + ArrayVel[BallColNr1] * BallTime;// Nalezenφ pozice koule 1
pb2 = OldPos[BallColNr2] + ArrayVel[BallColNr2] * BallTime;// Nalezenφ pozice koule 2
xaxis = (pb2 - pb1).unit();// Nalezenφ X_Axis
a = xaxis.dot(ArrayVel[BallColNr1]);// Nalezenφ projekce
U1x = xaxis * a;// Nalezenφ pr∙m∞t∙ vektor∙
U1y = ArrayVel[BallColNr1] - U1x;
xaxis = (pb1 - pb2).unit();
b = xaxis.dot(ArrayVel[BallColNr2]);// To samΘ pro druhou kouli
U2x = xaxis * b;
U2y = ArrayVel[BallColNr2] - U2x;
V1x = (U1x + U2x - (U1x - U2x)) * 0.5;// Nalezenφ nov²ch rychlostφ
V2x = (U1x + U2x - (U2x - U1x)) * 0.5;
V1y = U1y;
V2y = U2y;
for (j = 0; j < NrOfBalls; j++)// Aktualizace pozic vÜech koulφ
{
ArrayPos[j] = OldPos[j] + ArrayVel[j] * BallTime;
}
ArrayVel[BallColNr1] = V1x + V1y;// Nastavenφ prßv∞ vypoΦφtan²ch vektor∙ koulφm, kterΘ do sebe narazily
ArrayVel[BallColNr2] = V2x + V2y;
// Aktualizace pole explozφ
for(j = 0; j < 20; j++)// VÜechny exploze
{
if (ExplosionArray[j]._Alpha <= 0)// Hledß volnΘ mφsto
{
ExplosionArray[j]._Alpha = 1;// Nepr∙hlednß
ExplosionArray[j]._Position = ArrayPos[BallColNr1];// Pozice
ExplosionArray[j]._Scale = 1;// M∞°φtko
break;// UkonΦit prohledßvßnφ
}
}
continue;// Opakovat cyklus
}
}
// Konec test∙ kolizφ
// Pokud se proÜel cel² Φasov² ·sek a byly vypoΦteny reakce koulφ, kterΘ narazily
if (lamda != 10000)
{
RestTime -= lamda;// OdeΦtenφ Φasu kolize od ΦasovΘho ·seku
for (j = 0; j < NrOfBalls; j++)
{
ArrayPos[j] = OldPos[j] + ArrayVel[j] * lamda;
}
rt2 = ArrayVel[BallNr].mag();
ArrayVel[BallNr].unit();
ArrayVel[BallNr] = TVector::unit((normal * (2 * normal.dot(-ArrayVel[BallNr]))) + ArrayVel[BallNr]);
ArrayVel[BallNr] = ArrayVel[BallNr] * rt2;
// Aktualizace pole explozφ
for(j = 0; j < 20; j++)// VÜechny exploze
{
if (ExplosionArray[j]._Alpha <= 0)// Hledß volnΘ mφsto
{
ExplosionArray[j]._Alpha = 1;// Nepr∙hlednß
ExplosionArray[j]._Position = ArrayPos[BallColNr1];// Pozice
ExplosionArray[j]._Scale = 1;// M∞°φtko
break;// UkonΦit prohledßvßnφ
}
}
}
else
{
RestTime = 0;// UkonΦenφ hlavnφho cyklu a vlastn∞ i funkce
}
}
}
Jak jsem u₧ napsal na zaΦßtku, p°edm∞t kolizφ je velmi t∞₧k² a rozsßhl², aby se dal popsat jen v jednom tutorißlu, p°esto jste se nauΦili spoustu nov²ch v∞cφ. M∙₧ete zaΦφt vytvß°et vlastnφ p∙sobivß dema. Nynφ, kdy₧ chßpete zßklady, budete lΘpe rozum∞t i cizφm zdrojov²m k≤d∙m, kterΘ vßs zase posunou o kousek dßl. P°eji hodn∞ Üt∞stφ.
napsal: Dimitrios Christopoulos
p°elo₧il: Michal Turek - Woq
V souΦasnΘ dob∞ pracuje jako softwarov² in₧en²r virtußlnφ reality HelΘnskΘho sv∞ta v AtΘnßch/╪ecko (www.fhw.gr). AΦkoli se narodil v N∞mecku, studoval °eckou univerzitu Patras na bakalß°e p°φrodnφch v∞d v poΦφtaΦovΘm in₧en²rstvφ a informatice. Je takΘ dr₧itelem MSc degree (titul Magistra p°φrodnφch v∞d) z univerzity Hull (Anglie) v poΦφtaΦovΘ grafice a virtußlnφm prost°edφ.
Prvnφ kr∙Φky s programovßnφm podnikl v jazyce Basic na Commodoru 64. Po zaΦßtku studia se p°eorientoval na C/C++/Assembler na platform∞ PC. B∞hem n∞kolika minul²ch let si jako grafickΘ API zvolil OpenGL.
