

David Nikdel je osoba stojφcφ za tφmto skv∞l²m tutorißlem, ve kterΘm se nauΦφte, jak se vytvß°ejφ Bezierovy k°ivky. Dφky nim lze velice jednoduÜe zak°ivit povrch a provßd∞t jeho plynulou animaci pouhou modifikacφ n∞kolika kontrolnφch bod∙. Aby byl v²sledn² povrch modelu jeÜt∞ zajφmav∞jÜφ, je na n∞j namapovßna textura. Tutorißl takΘ eliminuje problΘmy s fullscreenem, kdy se po nßvratu do systΘmu neobnovilo p∙vodnφ rozliÜenφ obrazovky.
Tento tutorißl je od zaΦßtku zam²Ülen pouze jako ·vod do Bezierov²ch k°ivek, aby n∞kdo mnohem Üikovn∞jÜφ ne₧ jß dokßzal vytvo°it n∞co opravdu skv∞lΘho. Neberte ho jako kompletnφ Bezier knihovnu, ale spφÜe jako koncept, jak tyto k°ivky pracujφ a co dokß₧φ. TakΘ prosφm omluvte mou, v n∞kter²ch p°φpadech, ne a₧ tak sprßvnou terminologii. Doufßm, ₧e bude alespo≥ trochu srozumitelnß. Abych tak °ekl: Nikdo nenφ dokonal²...
Pochopit Bezierovy k°ivky s nulov²mi znalostmi matematiky je nemo₧nΘ. Proto bude nßsledovat maliΦko delÜφ sekce teorie, kterß by vßs m∞la do problematiky alespo≥ trochu zasv∞tit. Pokud vÜechno u₧ znßte, nic vßm nebrßnφ tuto nut(d)nou sekci p°eskoΦit a v∞novat se k≤du.
Bezierovy k°ivky b²vajφ primßrnφ metodou, jak v grafick²ch editorech Φi obyΦejn²ch programech vykreslovat zak°ivenΘ linky. Jsou obvykle reprezentovßny sΘriφ bod∙, z nich ka₧dΘ dva reprezentujφ teΦnu ke grafu funkce.

Toto je nejjednoduÜÜφ mo₧nß Bezierova k°ivka. DelÜφ jsou tvo°eny spojenφm n∞kolika dohromady. Je tvo°ena pouze Φty°mi body, dva konce a dva st°edovΘ kontrolnφ body. Pro poΦφtaΦ jsou vÜechny ·pln∞ stejnΘ, ale abychom si pomohli, spojujeme prvnφ a poslednφ dva. Linky budou v₧dy teΦnami k ukonΦovacφm bod∙m. ParametrickΘ k°ivky jsou kresleny nalezenφm libovolnΘho poΦtu bod∙ rovnom∞rn∞ rozprost°en²ch po k°ivce, kterΘ se spojφ Φßrami. PoΦtem bod∙ m∙₧eme ovlßdat hranatost k°ivky a samoz°ejm∞ takΘ dobu trvßnφ v²poΦt∙. Poda°φ-li se nßm mno₧stvφ bod∙ sprßvn∞ regulovat, pozorovatel v ka₧dΘm okam₧iku uvidφ perfektn∞ zak°iven² povrch bez trhßnφ animace.
VÜechny Bezierovy k°ivky jsou v zalo₧eny na zßkladnφm vzorci funkce. Komplikovan∞jÜφ verze jsou z n∞j odvozeny.
t + (1 - t) = 1
Vypadß jednoduÜe? Ano, rovnice jednoduchß urΦit∞ je, ale nesmφme zapomenout na to, ₧e je to pouze Bezierova k°ivka prvnφho stupn∞. Pou₧ijeme-li trochu terminologie: Bezierovy k°ivky jsou polynomißlnφ (mnohoΦlennΘ). Jak si zajistΘ pamatujete z algebry, prvnφ stupe≥ z polynomu je p°φmka - nic zajφmavΘho. Zßkladnφ funkce vychßzφ, dosadφme-li libovolnΘ Φφslo t. Rovnici m∙₧eme ovÜem takΘ mocnit na druhou, na t°etφ, na jakΘkoli Φφslo, proto₧e se ob∞ strany rovnajφ jednΘ. Zkusφme ji tedy umocnit na t°etφ.
(t + (1 - t))3 = 13
t3 + 3t2(1 - t) + 3t(1 - t)2 + (1 - t)3 = 1
Tuto rovnici pou₧ijeme k v²poΦtu mnohem vφce pou₧φvan∞jÜφ k°ivky - Bezierovy k°ivky t°etφho stupn∞. Pro toto rozhodnutφ existujφ dva d∙vody:
Zb²vß ale dodat jeÜt∞ jedna v∞c... Celß levß strana rovnice se rovnß jednΘ, tak₧e je bezpeΦnΘ p°edpoklßdat, ₧e pokud p°idßme vÜechny slo₧ky m∞la by se stßle rovnat jednΘ. Znφ to, jako by to mohlo b²t pou₧ito k rozhodnutφ kolik z ka₧dΘho kontrolnφho bodu lze pou₧φt p°i v²poΦtu bodu na k°ivce? (nßpov∞da: Prost∞ °ekni ano ;-) Ano. Sprßvn∞! Pokud chceme spoΦφtat hodnotu bodu v procentech vzdßlenosti na k°ivce, jednoduÜe nßsobφme ka₧dou slo₧ku kontrolnφm bodem (stejn∞ jako vektor) a nalezneme souΦet. Obecn∞ budeme pracovat s hodnotami 0 >= t >= 1, ale nenφ to technicky nutnΘ. Dokonale zmateni? Rad∞ji napφÜu tu funkci.
P1*t3 + P2*3*t2*(1-t) + P3*3*t*(1-t)2 + P4*(1-t)3 = Pnew
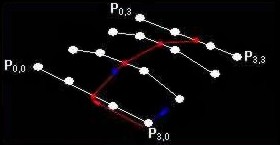
Proto₧e jsou polynomißly v₧dy spojitΘ, jsou dobrou cestou k pohybu mezi Φty°mi body. M∙₧eme dosßhnout ale v₧dy pouze okrajov²ch bod∙ (P1 a P4). Pokud tuto v∞tu nechßpete, podφvejte se na prvnφ obrßzek. V t∞chto p°φpadech se t = 0 pop°. t = 1.
To je sice hezkΘ, ale jak mßm pou₧φt Bezierovy k°ivky ve 3D? Je to docela jednoduchΘ. Pot°ebujeme 16 kontrolnφch bod∙ (4x4) a dv∞ prom∞nnΘ t a v. Vytvo°φme z nich Φty°i paralelnφ k°ivky. Na ka₧dΘ z nich spoΦφtßme jeden bod p°i urΦitΘm v a pou₧ijeme tyto Φty°i body k vytvo°enφ novΘ k°ivky a spoΦφtßme t. Nalezenφm vφce bod∙ m∙₧eme nakreslit triangle strip a tφm zobrazit Bezier∙v povrch.
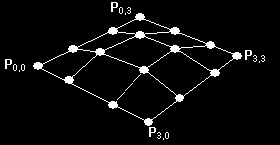
P°epoklßdßm, ₧e matematiky u₧ bylo dost. Poj∩me se vrhnout na k≤d tΘto lekce. ( Ze vÜeho nejd°φve vytvo°φme struktury. POINT_3D je obyΦejn² bod ve t°φrozm∞rnΘm prostoru. Druhß struktura je u₧ trochu zajφmav∞jÜφ - p°edstavuje Bezier∙v povrch. Anchors[4][4] je dvourozm∞rnΘ pole 16 °φdφcφch bod∙. Do display listu dlBPatch ulo₧φme v²sledn² model a texture uklßdß texturu, kterou na n∞j namapujeme.
typedef struct point_3d// Struktura bodu
{
double x, y, z;
} POINT_3D;
typedef struct bpatch// Struktura Bezierova povrchu
{
POINT_3D anchors[4][4];// M°φ₧ka °φdφcφch bod∙ (4x4)
GLuint dlBPatch;// Display list
GLuint texture;// Textura
} BEZIER_PATCH;
Mybezier je objektem prßv∞ vytvo°enΘ textury, rotz kontroluje ·hel natoΦenφ scΘny. ShowCPoints indikuje, jestli vykreslujeme m°φ₧ku mezi °φdφcφmi body nebo ne. Divs urΦuje hladkost (hranatost) v²slednΘho povrchu.
BEZIER_PATCH mybezier;// Bezier∙v povrch
GLfloat rotz = 0.0f;// Rotace na ose z
BOOL showCPoints = TRUE;// Flag pro zobrazenφ m°φ₧ky mezi kontrolnφmi body
int divs = 7;// PoΦet interpolacφ (mno₧stvφ vykreslovan²ch polygon∙)
Jestli si pamatujete, tak v ·vodu jsem psal, ₧e budeme maliΦko upravovat k≤d pro vytvß°enφ okna tak, aby se p°i nßvratu z fullscreenu obnovilo p∙vodnφ rozliÜenφ obrazovky (n∞kterΘ grafickΘ karty s tφm majφ problΘmy). DMsaved uklßdß p∙vodnφ nastavenφ monitoru p°ed vstupem do fullscreenu.
DEVMODE DMsaved;// Uklßdß p∙vodnφ nastavenφ monitoru
Nßsleduje n∞kolik pomocn²ch funkcφ pro jednoduchou vektorovou matematiku. SΦφtßnφ, nßsobenφ a vytvß°enφ 3D bod∙. Nic slo₧itΘho.
POINT_3D pointAdd(POINT_3D p, POINT_3D q)// SΦφtßnφ dvou bod∙
{
p.x += q.x;
p.y += q.y;
p.z += q.z;
return p;
}
POINT_3D pointTimes(double c, POINT_3D p)// Nßsobenφ bodu konstantou
{
p.x *= c;
p.y *= c;
p.z *= c;
return p;
}
POINT_3D makePoint(double a, double b, double c)// Vytvo°enφ bodu ze t°φ Φφsel
{
POINT_3D p;
p.x = a;
p.y = b;
p.z = c;
return p;
}
Funkcφ Bernstein() poΦφtßme bod, kter² le₧φ na Bezierov∞ k°ivce. V parametrech jφ p°edßvßme prom∞nnou u, kterß specifikuje procentußlnφ vzdßlenost bodu od okraje k°ivky vzhledem k jejφ dΘlce a pole Φty° bod∙, kterΘ jednoznaΦn∞ definujφ k°ivku. Vφcenßsobn²m volßnφm a krokovßnφm u v₧dy o stejn² p°φr∙stek m∙₧eme zφskat aproximaci k°ivky.
POINT_3D Bernstein(float u, POINT_3D *p)// SpoΦφtß sou°adnice bodu le₧φcφho na k°ivce
{
POINT_3D a, b, c, d, r;// PomocnΘ prom∞nnΘ
// V²poΦet podle vzorce
a = pointTimes(pow(u,3), p[0]);
b = pointTimes(3 * pow(u,2) * (1-u), p[1]);
c = pointTimes(3 * u * pow((1-u), 2), p[2]);
d = pointTimes(pow((1-u), 3), p[3]);
r = pointAdd(pointAdd(a, b), pointAdd(c, d));// SeΦtenφ nßsobk∙ a, b, c, d
return r;// Vrßcenφ v²slednΘho bodu
}
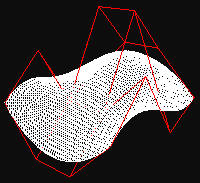
Nejv∞tÜφ Φßst prßce odvßdφ funkce genBezier(). SpoΦφtß k°ivky, vygeneruje triangle strip a v²sledek ulo₧φ do display listu. Pou₧itφ display listu je v tomto p°φpad∞ vφce ne₧ vhodnΘ, proto₧e nemusφme provßd∞t slo₧itΘ v²poΦty p°i ka₧dΘm framu, ale pouze p°i zm∞nßch vy₧ßdan²ch u₧ivatelem. Odstranφ se tφm zbyteΦnΘ zatφ₧enφ procesoru. Funkci p°edßvßme strukturu BEZIER_PATCH, v nφ₧ jsou ulo₧eny vÜechny pot°ebnΘ °φdφcφ body. Divs urΦuje kolikrßt budeme provßd∞t v²poΦty - ovlßdß hranatost v²slednΘho modelu. Nßsledujφcφ obrßzky jsou zφskßny p°epnutφm do re₧imu vykreslovßnφ linek mφsto polygon∙ (glPolygonMode(GL_FRONT_AND_BACK, GL_LINES)) a zakßzßnφm textur. Jasn∞ je vid∞t, ₧e Φφm je Φφslo v divs v∞tÜφ, tφm je objekt zaoblen∞jÜφ.



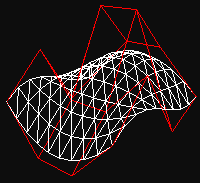
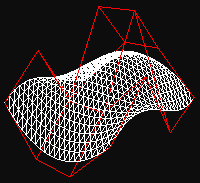
GLuint genBezier(BEZIER_PATCH patch, int divs)// Generuje display list Bezierova povrchu
{
Prom∞nnΘ u, v °φdφ cykly generujφcφ jednotlivΘ body na Bezierov∞ k°ivce a py, px, pyold jsou jejich procentußlnφ hodnoty, kterΘ slou₧φ k urΦenφ mφsta na k°ivce. Nab²vajφ hodnot v intervalu od 0 do 1, tak₧e je m∙₧eme bez komplikacφ pou₧φt i jako texturovacφ koordinßty. Drawlist je display list, do kterΘho kreslφme v²sledn² povrch. Do temp ulo₧φme Φty°i body pro zφskßnφ pomocnΘ Bezierovy k°ivky. DynamickΘ pole last uklßdß minul² °ßdek bod∙, proto₧e pro triangle strip pot°ebujeme dva °ßdky.
int u = 0, v;// ╪φdφcφ prom∞nnΘ
float py, px, pyold;// Procentußlnφ hodnoty
GLuint drawlist = glGenLists(1);// Display list
POINT_3D temp[4];// ╪φdφcφ body pomocnΘ k°ivky
POINT_3D* last = (POINT_3D*) malloc(sizeof(POINT_3D) * (divs+1));// Prvnφ °ada polygon∙
if (patch.dlBPatch != NULL)// Pokud existuje star² display list
glDeleteLists(patch.dlBPatch, 1);// Sma₧eme ho
temp[0] = patch.anchors[0][3];// Prvnφ odvozenß k°ivka (osa x)
temp[1] = patch.anchors[1][3];
temp[2] = patch.anchors[2][3];
temp[3] = patch.anchors[3][3];
for (v = 0; v <= divs; v++)// Vytvo°φ prvnφ °ßdek bod∙
{
px = ((float)v) / ((float)divs);// Px je procentußlnφ hodnota v
last[v] = Bernstein(px, temp);// SpoΦφtß bod na k°ivce ve vzdßlenosti px
}
glNewList(drawlist, GL_COMPILE);// Nov² display list
glBindTexture(GL_TEXTURE_2D, patch.texture);// Zvolφ texturu
Vn∞jÜφ cyklus prochßzφ °ßdky a vnit°nφ jednotlivΘ sloupce. Nebo to m∙₧e b²t i naopak. Zßle₧φ na tom, co si ka₧d² p°edstavφ pod pojmy °ßdek a sloupec :-)
for (u = 1; u <= divs; u++)// Prochßzφ body na k°ivce
{
py = ((float)u) / ((float)divs);// Py je procentußlnφ hodnota u
pyold = ((float)u - 1.0f) / ((float)divs);// Pyold mß hodnotu py p°i minulΘm pr∙chodu cyklem
V ka₧dΘm prvku pole patch.anchors[] mßme ulo₧eny Φty°i °φdφcφ body (dvourozm∞rnΘ pole). CelΘ pole dohromady tvo°φ Φty°i paralelnφ k°ivky, kterΘ si oznaΦφme jako °ßdky. Nynφ spoΦφtßme body, kterΘ jsou umφst∞ny na vÜech Φty°ech k°ivkßch ve stejnΘ vzdßlenosti py a ulo₧φme je do pole temp[], kterΘ p°edstavuje sloupec v °ßdku a celkov∞ tvo°φ Φty°i °φdφcφ body novΘ k°ivky pro sloupec.
Celou akci si p°edstavte jako trochu komplikovan∞jÜφ prochßzenφ dvourozm∞rnΘho pole - vn∞jÜφ cyklus prochßzφ °ßdky a vnit°nφ sloupce. Z upraven²ch °φdφcφch prom∞nn²ch si vybφrßme pozice bod∙ a texturovacφ koordinßty. Py s pyold p°edstavuje dva "rovn∞b∞₧nΘ" °ßdky a px sloupec. (P°ekl.: Ne₧ jsem tohle pochopil... v originßle o tom nebyla ani zmφnka).
temp[0] = Bernstein(py, patch.anchors[0]);// SpoΦφtß Bezierovy body pro k°ivku
temp[1] = Bernstein(py, patch.anchors[1]);
temp[2] = Bernstein(py, patch.anchors[2]);
temp[3] = Bernstein(py, patch.anchors[3]);
glBegin(GL_TRIANGLE_STRIP);// ZaΦßtek kreslenφ triangle stripu
for (v = 0; v <= divs; v++)// Prochßzφ body na k°ivce
{
px = ((float)v) / ((float)divs);// Px je procentußlnφ hodnota v
glTexCoord2f(pyold, px);// Texturovacφ koordinßty z minulΘho pr∙chodu
glVertex3d(last[v].x, last[v].y, last[v].z);// Bod z minulΘho pr∙chodu
Do pole last nynφ ulo₧φme novΘ hodnoty, kterΘ se p°i dalÜφm pr∙chodu cyklem stanou op∞t star²mi.
last[v] = Bernstein(px, temp);// Generuje nov² bod
glTexCoord2f(py, px);// NovΘ texturovΘ koordinßty
glVertex3d(last[v].x, last[v].y, last[v].z);// Nov² bod
}
glEnd();// Konec triangle stripu
}
glEndList();// Konec display listu
free(last);// Uvolnφ dynamickΘ pole vertex∙
return drawlist;// Vrßtφ prßv∞ vytvo°en² display list
}
Jedinß v∞c, kterou ned∞lßme, ale kterß by se urΦit∞ mohla hodit, jsou normßlovΘ vektory pro sv∞tlo. Kdy₧ na n∞ p°ijde, mßme dv∞ mo₧nosti. V prvnφ nalezneme st°ed ka₧dΘho troj·helnφku, aplikujeme na n∞j n∞kolik v²poΦtu k zφskßnφm teΦen k Bezierov∞ k°ivce na osßch x a y, vektorov∞ je vynßsobφme a tφm zφskßme vektor kolm² souΦasn∞ k ob∞ma teΦnßm. Po normalizovßnφ ho m∙₧eme pou₧φt jako normßlu. Druh² zp∙sob je rychlejÜφ a jednoduÜÜφ, ale mΘn∞ p°esn². M∙₧eme cheatovat a pou₧φt normßlov² vektor troj·helnφku (spoΦφtan² libovoln²m zp∙sobem). Tφm zφskßme docela dobrou aproximaci. Osobn∞ preferuji druhou, jednoduÜÜφ cestu, kterß ovÜem nevypadß tak realistiky.
Ve funkci initBezier() inicializujeme matici kontrolnφch bod∙ na v²chozφ hodnoty. Pohrajte si s nimi, a¥ vidφte, jak jednoduÜe se dajφ m∞nit tvary povrch∙.
void initBezier(void)// PoΦßteΦnφ nastavenφ kontrolnφch bod∙
{
mybezier.anchors[0][0] = makePoint(-0.75,-0.75,-0.5);
mybezier.anchors[0][1] = makePoint(-0.25,-0.75, 0.0);
mybezier.anchors[0][2] = makePoint( 0.25,-0.75, 0.0);
mybezier.anchors[0][3] = makePoint( 0.75,-0.75,-0.5);
mybezier.anchors[1][0] = makePoint(-0.75,-0.25,-0.75);
mybezier.anchors[1][1] = makePoint(-0.25,-0.25, 0.5);
mybezier.anchors[1][2] = makePoint( 0.25,-0.25, 0.5);
mybezier.anchors[1][3] = makePoint( 0.75,-0.25,-0.75);
mybezier.anchors[2][0] = makePoint(-0.75, 0.25, 0.0);
mybezier.anchors[2][1] = makePoint(-0.25, 0.25,-0.5);
mybezier.anchors[2][2] = makePoint( 0.25, 0.25,-0.5);
mybezier.anchors[2][3] = makePoint( 0.75, 0.25, 0.0);
mybezier.anchors[3][0] = makePoint(-0.75, 0.75,-0.5);
mybezier.anchors[3][1] = makePoint(-0.25, 0.75,-1.0);
mybezier.anchors[3][2] = makePoint( 0.25, 0.75,-1.0);
mybezier.anchors[3][3] = makePoint( 0.75, 0.75,-0.5);
mybezier.dlBPatch = NULL;// Display list jeÜt∞ neexistuje
}
InitGL() je celkem standardnφ. Na jejφm konci zavolßme funkce pro inicializaci kontrolnφch bod∙, nahrßnφ textury a vygenerovßnφ display listu Bezierova povrchu.
int InitGL(GLvoid)// Inicializace
{
glEnable(GL_TEXTURE_2D);// Zapne texturovßnφ
glShadeModel(GL_SMOOTH);// JemnΘ stφnovßnφ
glClearDepth(1.0f);// Nastavenφ hloubkovΘho bufferu
glEnable(GL_DEPTH_TEST);// Zapne testovßnφ hloubky
glDepthFunc(GL_LEQUAL);// Typ testovßnφ hloubky
glClearColor(0.0f, 0.0f, 0.0f, 0.5f);// ╚ernΘ pozadφ
glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST);// Perspektivnφ korekce
initBezier();// Inicializace kontrolnφch bod∙
LoadGLTexture(&(mybezier.texture), "./data/NeHe.bmp");// Loading textury
mybezier.dlBPatch = genBezier(mybezier, divs);// Generuje display list Bezierova povrchu
return TRUE;// Inicializace v po°ßdku
}
Vykreslovßnφ nenφ oproti minul²m tutorißl∙m v∙bec slo₧itΘ. Po vÜech translacφch a rotacφch zavolßme display list a potom p°φpadn∞ propojφme °φdφcφ body Φerven²mi Φarami. Chcete-li linky zapnout nebo vypnout stiskn∞te mezernφk.
int DrawGLScene(GLvoid)// VÜechno kreslenφ
{
int i, j;// ╪φdφcφ prom∞nnΘ cykl∙
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);// Sma₧e obrazovku a hloubkov² buffer
glLoadIdentity();// Reset matice
glTranslatef(0.0f, 0.0f, -4.0f);// P°esun do hloubky
glRotatef(-75.0f, 1.0f, 0.0f, 0.0f);// Rotace na ose x
glRotatef(rotz, 0.0f, 0.0f, 1.0f);// Rotace na ose z
glCallList(mybezier.dlBPatch);// Vykreslφ display list Bezierova povrchu
if (showCPoints)// Pokud je zapnutΘ vykreslovßnφ m°φ₧ky
{
glDisable(GL_TEXTURE_2D);// Vypne texturovßnφ
glColor3f(1.0f, 0.0f, 0.0f);// ╚ervenß barva
for(i = 0; i < 4; i++)// Horizontßlnφ linky
{
glBegin(GL_LINE_STRIP);// Kreslenφ linek
for(j = 0; j < 4; j++)// ╚ty°i linky
{
glVertex3d(mybezier.anchors[i][j].x, mybezier.anchors[i][j].y, mybezier.anchors[i][j].z);
}
glEnd();// Konec kreslenφ
}
for(i = 0; i < 4; i++)// Vertikßlnφ linky
{
glBegin(GL_LINE_STRIP);// Kreslenφ linek
for(j = 0; j < 4; j++)// ╚ty°i linky
{
glVertex3d(mybezier.anchors[j][i].x, mybezier.anchors[j][i].y, mybezier.anchors[j][i].z);
}
glEnd();// Konec kreslenφ
}
glColor3f(1.0f, 1.0f, 1.0f);// Bφlß barva
glEnable(GL_TEXTURE_2D);// Zapne texturovßnφ
}
return TRUE;// V po°ßdku
}
Prßci s Bezierov²mi k°ivkami jsme ·sp∞Ün∞ dokonΦili, ale jeÜt∞ nesmφme zapomenout na fullscreen fix. Odstra≥uje problΘm s p°epφnßm z fullscreenu do okennφho m≤du, kdy n∞kterΘ grafickΘ karty sprßvn∞ neobnovujφ p∙vodnφ rozliÜenφ obrazovky (nap°. moje sta°iΦkß ATI Rage PRO a n∞kolik dalÜφch). Doufßm, ₧e budete pou₧φvat tento pozm∞n∞n² k≤d, aby si ka₧d² mohl bez komplikacφ vychutnat vaÜe skv∞lß OpenGL dema. V tutorißlu jsme provedli celkem t°i zm∞ny. Prvnφ p°i deklaraci prom∞nn²ch, kdy jsme vytvo°ili prom∞nnou DEVMODE DMsaved. Druhou najdete v CreateGLWindow(), kde jsme tuto pomocnou strukturu naplnili informacemi o aktußlnφm nastavenφ. T°etφ zm∞na je v KillGLWindow(), kde se obnovuje p∙vodnφ ulo₧enΘ nastavenφ.
BOOL CreateGLWindow(char* title, int width, int height, int bits, bool fullscreenflag)// Vytvß°enφ okna
{
// Deklarace prom∞nn²ch
EnumDisplaySettings(NULL, ENUM_CURRENT_SETTINGS, &DMsaved);// Ulo₧φ aktußlnφ nastavenφ obrazovky
// VÜe ostatnφ z∙stßvß stejnΘ
}
GLvoid KillGLWindow(GLvoid)// Zav°enφ okna
{
if (fullscreen)// Jsme ve fullscreenu?
{
if (!ChangeDisplaySettings(NULL, CDS_TEST))// Pokud pokusnß zm∞na nefunguje
{
ChangeDisplaySettings(NULL, CDS_RESET);// Odstranφ hodnoty z registr∙
ChangeDisplaySettings(&DMsaved, CDS_RESET);// Pou₧ije ulo₧enΘ nastavenφ
}
else
{
ChangeDisplaySettings(NULL, CDS_RESET);
}
ShowCursor(TRUE);// Zobrazφ ukazatel myÜi
}
// VÜe ostatnφ z∙stßvß stejnΘ
}
Poslednφ v∞cφ jsou u₧ standardnφ testy stisku klßves.
// Funkce WinMain()
if (keys[VK_LEFT])// èipka doleva
{
rotz -= 0.8f;// Rotace doleva
}
if (keys[VK_RIGHT])// èipka doprava
{
rotz += 0.8f;// Rotace doprava
}
if (keys[VK_UP])// èipka nahoru
{
divs++;// MenÜφ hranatost povrchu
mybezier.dlBPatch = genBezier(mybezier, divs);// Aktualizace display listu
keys[VK_UP] = FALSE;
}
if (keys[VK_DOWN] && divs > 1)// èipka dol∙
{
divs--;// V∞tÜφ hranatost povrchu
mybezier.dlBPatch = genBezier(mybezier, divs);// Aktualizace display listu
keys[VK_DOWN] = FALSE;
}
if (keys[VK_SPACE])// Mezernφk
{
showCPoints = !showCPoints;// Zobrazφ/skryje linky mezi °φdφcφmi body
keys[VK_SPACE] = FALSE;
}
Doufßm, ₧e pro vßs byl tento tutorißl pouΦn² a ₧e od nyn∞jÜka miluje Bezierovy k°ivky stejn∞ jako jß ;-) JeÜt∞ jsem se o tom nezmφnil, ale mnohΘ z vßs jist∞ napadlo, ₧e se s nimi dß vytvo°it perfektnφ morfovacφ efekt. A velmi jednoduÜe! Nezapome≥te, se m∞nφ poloha pouze Üestnßcti bod∙. Zkuste o tom pop°em²Ület...
napsal: David Nikdel
p°elo₧il: Michal Turek - Woq
