Tento Φlßnek vychßzφ z m²ch zßpisk∙ do matematiky z druhΘho roΦnφku na st°ednφ Ükole. Jo, na diktovßnφ byla Wakuovka v₧dycky dobrß... Tehdy jsem moc nechßpal k Φemu mi tento obor matematiky v∙bec bude, ale kdy₧ jsem se zaΦal v∞novat OpenGL, zßhy jsem pochopil. Zkuste si vzφt nap°φklad 27. lekci NeHe Tutorißl∙. Bez znalostφ 3D matematiky nemßte Üanci. Doufßm, ₧e vßm tento Φlßnek pom∙₧e alespo≥ se zßklady a pochopenφm princip∙.
Tak tedy zaΦneme. Co je geometrie vφ snad ka₧d². Ale co je analytickß geometrie? Dala by se definovat velice jednoduÜe: Analytickß geometrie °eÜφ v²poΦtem to, co se dß nakreslit. A p°esn∞ o to se v poΦφtaΦovΘ grafice jednß. Pro vÜechny v²poΦty je nutnß soustava sou°adnic. Tvo°φ ji dv∞ (pop°. t°i) navzßjem kolmΘ osy, kterΘ majφ stejn∞ velkΘ jednotky.
NejjednoduÜÜφm ·tvarem je bod. Nemß ₧ßdn² rozm∞r, ale pouze polohu. Jeho poloha mß ve dvourozm∞rnΘm systΘmu dv∞ slo₧ky, ve t°φrozm∞rnΘm t°i atd. Formßln∞ se zapisuje takto: JM╔NO BODU[x, y]. V nßsledujφcφm p°φkladu by se uvedenΘ body definovaly takto:
A[-2; 1]
B[ 3; 1]
C[-2; 3]
S[ ?; ?]// Je st°edem ·seΦky BC
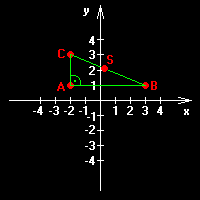
Bod S jsme nedefinovali, proto₧e jen tak od oka jeho slo₧ky neurΦφme. Vφme pouze, ₧e je st°edem ·seΦky BC a chceme urΦit polohu. V p°φpad∞ grafickΘ metody bychom si vzali papφr, tu₧ku a pravφtko, nakreslili bychom sou°adnicovΘ osy, vepsali body a spojili je ·seΦkami. Dßle bychom zm∞°ili dΘlku ·seΦky BC, vyd∞lili ji dv∞ma a tuto vypoΦφtanou vzdßlenost nanesli (je jedno, zda z bodu B nebo C, proto₧e S je v polovin∞). OdeΦteme jednotlivΘ x, y slo₧ky a zφskßme polohu bodu S.
Jinß je ale situace, kdybychom nem∞li ₧ßdnΘ pom∙cky a museli vÜechno spoΦφtat. Z obrßzku jde na prvnφ pohled vid∞t, ₧e x-ovß slo₧ka bodu S je pr∙m∞rem x-ov²ch slo₧ek bodu B a C. Y-ovß slo₧ka je to samΘ. M∙₧eme tedy vytvo°it vzorec a dosadit hodnoty. Porovnßme-li v²sledek S[0,5; 2] s obrßzkem, sou°adnice odpovφdajφ. Od nyn∞jÜka budeme pou₧φvat pouze poΦetnφ metodu.
S[x; y] = [((xB + xC] / 2); ((yB + yC) / 2)]
S[((3 - 2)) / 2); ((1 + 3) / 2)]
S[0,5; 2]
Druh²m problΘmem m∙₧e b²t, pokud chceme zjistit dΘlku ·seΦky BC. Op∞t se podφvßme na obrßzek a na prvnφ pohled vidφme :-), ₧e ·seΦka BC je p°eponou pravo·hlΘho troj·helnφku ABC, pro kter² platφ Pythagorova v∞ta.
c2 = a2 + b2
c = sqrt(a2 + b2)// sqrt(x) = druhß odmocnina z x
Dß se °φct, ₧e nßsledujφcφ vzorec by platil i tehdy, pokud by troj·helnφk ABC nebyl pravo·hl² a dokonce i tehdy, pokud bychom nem∞li v∙bec ₧ßdn² troj·helnφk, ale pouze ·seΦku BC. Prav²m ·hlem je v tomto p°φpad∞ kolmost sou°adnicov²ch os, dΘlky stran a, c zastupujφ pr∙m∞ty ·seΦky do os x, y. Pythagorova v∞ta tedy stßle platφ.
|BC| = sqrt((xB - xC)2 + (yB - yC)2)
|BC| = sqrt(52 + (-2)2)
|BC| = sqrt(25 + 4)
|BC| = sqrt(29)
|BC| = 5,3851
Vektory obecn∞ urΦujφ, jak se zm∞nφ slo₧ky sou°adnic x a y ne₧ se p°esuneme z poΦßtku vektoru na jeho konec. ZnaΦφ se Üipkou sm∞°ujφcφ zleva doprava (od poΦßteΦnφho do koncovΘho bodu) nad jmΘnem vektoru. Pozn.: V tomto Φlßnku ho znaΦφm pouze Φßrou, proto₧e nemohu p°ijφt na to, jak v HTML vytvo°it Üipku. Narozdφl od bodu, kter² se umφs¥uje do hranat²ch, pφÜeme slo₧ky vektoru do obyΦejn²ch kulat²ch zßvorek. Chceme-li zjistit vektor BC odeΦteme od koncovΘho bodu, poΦßtek.
BC = ((xC - xB); (yC - yB))
BC = ((-2 -3); (3-1))
BC = (-5; 2)
Dva stejnΘ vektory (stejn∞ velkΘ a stejn∞ orientovanΘ) p°edstavujφ v matematice dv∞ r∙znß umφst∞nφ tΘho₧ vektoru. Z toho plyne, ₧e vektor m∙₧eme p°enΘst kamkoli na rovnob∞₧nou p°φmku, akorßt nesmφme zm∞nit jeho velikost. Toto ale neplatφ ve fyzice, kde se u vektoru, krom∞ velikosti musφ urΦit i poΦßtek nebo konec (nap°. p∙sobiÜt∞ sφly).
P°i zjiÜ¥ovßnφ velikosti vektoru se postupuje ·pln∞ stejn∞ jako p°i urΦovßnφ dΘlky ·seΦky.
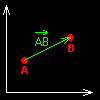
|AB| = sqrt((xB - xA)2 + (yB - yA)2)
V₧dy seΦteme zvlßÜ¥ x-ovΘ a zvlßÜ¥ y-slo₧ky. Nic t∞₧kΘho.
a = (-3; 2)
b = ( 4; 6)
a + b = ( 1; 8)
a - b = (-7;-4)
Op∞t vynßsobφme zvlßÜ¥ jednotlivΘ slo₧ky.
4 * a = (4 * xa; 4 * ya)
4 * a = (-12; 8)
u * v = uX*vX + uY*vY
Nebo takΘ
u * v = |u| * |v| * cos uhel
Ze vzorce pro v²poΦet skalßrnφho souΦinu vektor∙ (viz. v²Üe) lze odvodit vztah pro v²poΦet ·hlu dvou vektor∙.
cos uhel = (u * v) / (|u| * |v|)
Dosadφme-li do rovnice d°φve uvedenΘ vzorce, zφskßme v²sledn² vztah:

Vynßsobφme-li vektorov∞ dva vektory, zφskßme vektor t°etφ, kter² je kolm² k rovin∞ urΦenΘ p∙vodnφmi dv∞ma vektory. Aby bylo mo₧no urΦit vektorov² souΦin, nesmφ b²t vektory u a v rovnob∞₧nΘ, proto₧e by netvo°ily rovinu. Vektorov² souΦin se neznaΦφ operßtorem *, ale x.
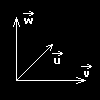
u = (-3; 5; -1)
v = ( 1; 2; -4)

Nynφ polo₧φme vektory i, j, k rovny jednΘ (jednotkovΘ vektory). Nßsobenφm jedniΦkou se koeficienty nezm∞nφ, tak₧e jsme prßv∞ zφskali v²sledek.
w = (-18; -13; -11)
Dimenze (rozm∞r) vektorovΘho prostoru urΦuje maximßlnφ poΦet lineßrn∞ nezßvisl²ch vektor∙. Je takΘ dßna poΦtem slo₧ek sou°adnice. Vektory jsou lineßrn∞ zßvislΘ, kdy₧ pro libovoln² vektor soustavy vektor∙ platφ:
v1, v2, v3 ... vn
vm = k1*v1 + k2*v2 + ... + kn*vn
Pro lineßrn∞ nezßvislΘ vektory tato rovnice neplatφ pro ₧ßdn² vektor systΘmu.
Jednorozm∞rn² prostor mß pouze jeden nezßvisl² vektor. Ostatnφ vektory na p°φmce se dajφ pomocφ tohoto vektoru vyjßd°it.
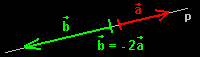
Mß dva lineßrn∞ nezßvislΘ vektory.
Mß t°i lineßrn∞ nezßvislΘ vektory. Myslφm, ₧e podstatu u₧ chßpete. Tyto vlastnosti se vyu₧φvajφ k °eÜenφ systΘmu N rovnic o N neznßm²ch.
Dva kolmΘ vektory v rovin∞ majφ obrßcenΘ po°adφ slo₧ek a u jednΘ z nich (jedno kterΘ) opaΦnΘ znamΘnko. Kolm² vektor k zadanΘmu vektoru je rovn∞₧ libovoln² k-nßsobek vektoru zφskanΘho uveden²m postupem. Odvozenφ tΘto definice vychßzφ ze vzorce pro ·hel dvou vektor∙, kde se za ·hel dosadφ 90░.
a = ( 3; 2)
b = ( ?; ?)// Je kolm² k a
b = ( 2;-3)
b = (-2; 3)
b = (-4; 6)// Atd.
Nßsledujφcφ vzorec je parametrickou rovnicφ p°φmky.
p:
x = AX + sX*t
y = AY + sY*t
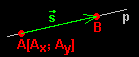
A[2; 4]
s = (5; 7)
p:
x = 2 + 5*t
y = 4 + 7*t
Toto u₧ by m∞lo b²t jasnΘ, ale myslφm si, ₧e malß ukßzka Ükodit nebude. Je ·pln∞ jedno, zda po zφskßnφ vektoru dosadφme do rovnice sou°adnice bodu A nebo B, proto₧e oba le₧φ na hledanΘ p°φmce.
A[2; 4]
B[5; 3]
s = B - A = (5-2; 3-4) = (3; -1)
p:
x = 2 + 3*t
y = 4 - t
A jeÜt∞ si zkusφme, zda bod C[1; 2] na tΘto p°φmce le₧φ nebo ne. Za x a y dosadφme jeho sou°adnice a pokud se budou parametry t v obou rovnicφch rovnat, C le₧φ na p°φmce.
p:
1 = 2 + 3*t => 3*t = -1 => t = -1/3
2 = 4 - t => -t = -2 => t = 2
V prvnφ rovnici vyÜlo t rovno -1/3 v druhΘ se t rovnalo 2. Z toho plyne, ₧e bod C nele₧φ na p°φmce t.
Nev²hoda parametrickΘho vyjßd°enφ je v tom, ₧e na prvnφ pohled nepoznßme, jestli se jednß u dvou soustav rovnic o tutΘ₧ p°φmku nebo ne.
P°edem se omlouvßm za to, ale vÜechno bude pouze teoreticky, proto₧e psanφ p°φklad∙ v HTML mi u₧ leze opravdu na nervy.
Rovnici p°φmky sestavit umφme, ale jak bychom postupovali p°i hledßnφ rovnice p°φmky, kterß je rovnob∞₧nß ke znßmΘ p°φmce v urΦitΘm bod∞? Vychßzφme z toho, ₧e rovnob∞₧nΘ p°φmky mohou mφt stejnΘ sm∞rovΘ vektory, tak₧e pouze nahradφme sou°adnice bodu v rovnicφch.
U kolmΘ p°φmky by se op∞t nahradily sou°adnice bodu, ale navφc bychom jeÜt∞ museli zm∞nit vektor na kolm² - nic t∞₧kΘho (viz. kolmΘ vektory).
Pr∙seΦφk dvou p°φmek je spoleΦn²m °eÜenφm dvou rovnic p°φmek. V parametrickΘm tvaru porovnßme sou°. x prvnφ p°φmky se sou°. x druhΘ p°φmky. VypoΦteme parametr t a jestli platφ rovnost i pro sou°adnice y p°i stejnΘm t, je tento parametr p°φsluÜn² k pr∙seΦφku. Dosazenφm parametru do rovnic dostaneme sou°adnice pr∙seΦφku.
┌hel dvou p°φmek je ·hlem mezi dv∞ma sm∞rov²mi vektory (viz. ┌hel dvou vektor∙).
Nφ₧e je uveden jejφ vzorec. Prom∞nnΘ x a y jsou sou°adnice bodu, kter² le₧φ na p°φmce. A, b jsou slo₧ky normßlovΘho vektoru p°φmky.
p: a*x + b*y + c = 0
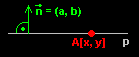
Nejprve vypoΦφtßme sm∞rov² vektor a ten p°evedeme na normßlov². Tφm zφskßme prom∞nnΘ a, b, x, y. Z∙stane nßm jednoduchß rovnice o jednΘ neznßmΘ. VypoΦteme c a dosadφme do p∙vodnφ rovnice
A[2; 4]
B[5; 3]
s = AB = (5-2; 3-4) = (3; -1)// Sm∞rov² vektor
n = (1; 3)// Normßlov² vektor
Zφskali jsme Φφsla a = 1, b = 3 a pou₧ijeme nap°. slo₧ky bodu A (je to jedno). VÜe dosadφme do rovnice p°φmky a hledßme Φφslo c.
p: a*x + b*y + c = 0
p: 1*2 + 3*4 + c = 0
c = - (1*2 + 3*4) = - (2 + 12) = -14
Nakonec dosadφme do rovnice p°φmky Φφsla a, b, c a mßme v²sledek.
p: x + 3y - 14 = 0// V²slednß rovnice p°φmky
JeÜt∞ jedna poznßmka na konec. Je-li sm∞rov² (pop°. normßlov²) vektor zadßn tak, ₧e jeho slo₧ky se dajφ rozÜφ°it nebo krßtit, m∙₧eme za n∞j zvolit jeho libovoln² k nßsobek. Nßsledujφcφ dv∞ rovnice p°φmek jsou tedy toto₧nΘ:
p: -4x + 8y + 24 = 0
p: -x + 2y + 6 = 0// Vykrßcenß verze
Hledßme rovnob∞₧ku q s p°φmkou p: x - 2y + 3 = 0, kterß prochßzφ bodem M[2; 5]. StaΦφ dosadit sou°adnice bodu M do rovnice p a vypoΦφtat Φφslo c, kterΘ dosadφme do p∙vodnφ rovnice p. VÜimn∞te si, ₧e se p°φmky liÜφ pouze Φφslem c.
q: x - 2y + c = 0
2 - 2*5 + c = 0
c = 8
q: x - 2y + 8 = 0// P°φmka q je rovnob∞₧nß s p
p: x - 2y + 3 = 0
Op∞t pouze postup: Vytvo°φ se kolm² vektor k normßlovΘmu vektoru p∙vodnφ p°φmky. Spolu s bodem, kter²m mß kolmß p°φmka prochßzet, se dosadφ do rovnice a vypoΦφtß se c. P°φklad dvou kolm²ch p°φmek:
p: 5x - 6y + 4 = 0
q: 6x + 5y -15 = 0
Stejn∞ jako rovnob∞₧nΘ p°φmky, jsou si takΘ trochu podobnΘ...
Sm∞rnicov² tvar rovnice p°φmky se u₧φvß tam, kde je zadßn sklon p°φmky vzhledem k ose x nebo je-li sm∞rnice vypoΦtena jin²m zp∙sobem (nap°. derivacφ). ╚φslo q v nßsledujφcφ rovnici oznaΦuje ·sek na ose y, kde ji p°φmka protφnß. K je sm∞rnice p°φmky, kterß se vypoΦφtß goniometrickou funkcφ k = tg a. Je to takΘ derivace jakΘkoli funkce - tedy teΦna k jejφmu grafu.
y = k*x + q
Nebo takΘ:
y - yA = k * (x - xA)
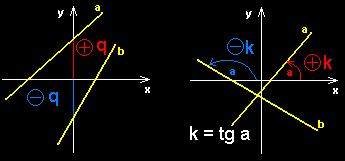
Vychßzφme z toho, ₧e k = tg a. Postup zjiÜt∞nφ tg a vysv∞tluje obrßzek.

Po zjiÜt∞nφ Φφsla k nßm u₧ nic nebrßnφ tomu, abychom ho spolu se slo₧kami bodu A nebo B dosadili do rovnice a zφskali q.
Rovnob∞₧nΘ p°φmky majφ v rovnicφch stejnou hodnotu k, liÜφ se v q. Kolmice majφ v k zßpornou p°evrßcenou hodnotu. To znamenß, ₧e pokud je u jednΘ nap°φklad k = 2, u druhΘ bude k = - 1/2.
╚φsla a, b, c jsou konstanty z rovnice p°φmky v obecnΘm tvaru a Φφsla x, y jsou sou°adnice bodu. StaΦφ pak dosadit do vzorce.
Vzdßlenost dvou rovnob∞₧ek lze zjistit ·pln∞ stejn∞. Nejd°φve zφskßme bod, kter² le₧φ na jednΘ z nich a pak op∞t dosadφme do vzorce.
Jsou skoro stejnΘ jako parametrickΘ rovnice p°φmky. Nßsleduje vzorec a p°φklad.
R:
x = AX + kX*u + lX*v
y = AY + kY*u + lZ*v
z = AZ + kY*u + lZ*v
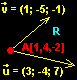
R:
x = 1 + 3k +l
y = 4 - 4k - 5l
z = -2 + 7k - l
Vzorec je analogick² vzorci obecnΘ rovnice p°φmky. ╚φsla a, b, c jsou slo₧ky normßlovΘho vektoru roviny a Φφsla x, y, z jsou sou°adnice bodu, kter² na nφ le₧φ. Stejn∞ jako se u p°φmky dopoΦφtßvalo c, nynφ se musφ spoΦφtat d - ₧ßdn² problΘm, vÜe u₧ znßme.
R: ax + by + cz + d = 0
Dßme si jeden p°φklad a zßrove≥ ho teoreticky! vy°eÜφme. UrΦete rovnici roviny R, kterß je dßna body K[-2; 1; 1], L[0; 3; -5]; M[4; -6; 9]. Postupujeme tak, ₧e urΦφme jeden bod jako zßkladnφ, nap°φklad K a urΦφme vektory KL a KM. Pot°ebujeme urΦit vektor, kter² je kolm² k ob∞ma najednou. Zφskßme ho vektorov²m souΦinem vektor∙ n = KL x KM. V²sledek dosadφme do rovnice roviny a vypoΦφtßme neznßmou d.
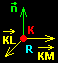
Jeden bod v rovin∞ (poΦßtek sou°adnic) mß sou°adnice 0[0; 0; 0]. Z toho plyne, ₧e:
R: a*x + b*y + c*z + d = 0
R: a*0 + b*0 + c*0 + d = 0
d = 0// V²slednß rovnice roviny
Chybφ koeficient u prom∞nnΘ, kterß pat°φ ke konkrΘtnφ ose.
R: 3y - 2z + 5 = 0// Rovina rovnob∞₧nß s osou x
U obou chybφ koeficienty a t°etφ slo₧ka je konstantnφ.
R: 3z + 5 = 0// Rovina rovnob∞₧nß s osami x a y
z = - 5/3
z = konst.
Ka₧dß rovina je zadßna v₧dy t°emi nezßvisl²mi prvky:
V rovin∞ mohla b²t p°φmka vyjßd°ena mnoha zp∙soby, kterΘ se v prostoru smrskly na jedin² mo₧n² zp∙sob - parametrickΘ rovnice.
Tohle u₧ znßme, tak₧e to nebudu zbyteΦn∞ rozepisovat, p°idßvß se pouze dalÜφ rovnice pro osu z.
p:
x = AX + sX*t
y = AY + sY*t
z = AZ + sZ*t
Hledßme-li p°φmku jako pr∙seΦnici dvou rovin, zvolφme dva body, kterΘ le₧φ souΦasn∞ v obou rovinßch - tj. jednu sou°adnici zvolφme a ostatnφ dv∞ musφ vyhovovat rovnicφm obou rovin. Pak staΦφ vytvo°it sm∞rov² vektor a nßsledn∞ ho s jednφm z bod∙ dosadit do parametrick²ch rovin p°φmek.
... a nynφ byste m∞li rozum∞t alespo≥ zßklad∙m analytickΘ geometrie. My jsme toto uΦivo brali ve Ükole skoro Φtvrt roku, tak₧e tento Φlßnek berte jako struΦn²!!! v²tah. Pokud se vßm zdß, ₧e je vÜe jakoby useknutΘ, mßte pravdu. Jak to tak b²vß, skonΦil Ükolnφ rok a na zaΦßtku dalÜφho u₧ se nepokraΦovalo. TakΘ musφm poznamenat, ₧e ke ka₧dΘho tΘmatu mßme v seÜit∞ n∞kolik p°φklad∙, ale opisovat je sem by se s nejv∞tÜφ pravd∞podobnostφ stalo mojφ noΦnφ m∙rou - d∞kuji za pochopenφ... nebo jinak °eΦeno: Bu∩te rßdi za to, co tady mßte, psal jsem to skoro t²den, Φty°i hodiny denn∞ :-)
napsal: Michal Turek - Woq