| Jurníček Software | Porter |
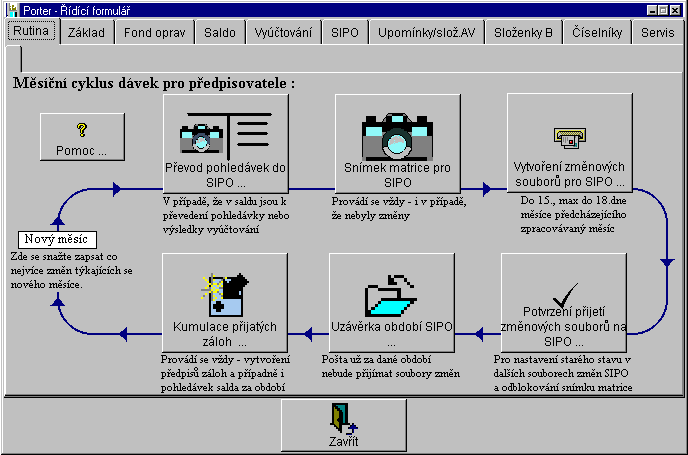
Na kartě "Rutina" řídícího formuláře je znázorněn měsíčně prováděný cyklus činností a tlačítka dávkových operací které je zpravidla nutno provést každý měsíc:

Vyjímku z tohoto pravidla tvoří převod pohledávek salda do SIPO - tuto akci budete potřebovat pouze v případě, že
Převod pohledávek salda do SIPO jsem do schematu zařadil proto, abych ozřejmil, v které fázi zpracování bude prováděn, pokud to bude potřeba. Zde je však nutno poznamenat, že je vcelku lhostejno, zda převod pohledávek do SIPO provedete před snímkem matrice, nebo po něm - obojí ovšem musí být následováno vytvořením změnových souborů a jejich přijetím na kontaktním místě, má-li to mít dopad na stav kmene SIPO.
Nyní tedy podrobněji k postupu zpracování období :
Stav poplatků předpisu záloh za (zpracovávané) období nastavuje obsluha v matrici. Snažte se co nejvíce změn týkajících se správy, vlastnictví jednotek (stěhování a výměny bytů, změny záloh nebo jiných složek předpisu) zapsat do dat v intervalu mezi kumulací za předchozí období a uzávěrkou období SIPO za zpracovávné období. Takto se bude stav na SIPO (u vlastníků jednotek platících přes SIPO) shodovat se skutečným stavem, tedy s předpisem záloh.
Snímkem matrice pro SIPO nastavujete interní obraz kmene SIPO. S tímto interním obrazem kmene SIPO je pak změnovými soubory synchronizován kmen SIPO na poště.
Snímek matrice pro SIPO vytváříte vždy - i v případě, že k žádným změnám nedošlo, ledaže byste neměli žádného vlastníka platícího přes SIPO. Naproti tomu převod pohledávek ze salda do SIPO provádíte pouze v případě, že takové pohledávky máte (zpětné doplatky, výsledek vyúčtování).
Jak jsem napsal, práci si ušetříte tehdy, když co nejvíce změn promítnete do SIPO. Nicméně se může stát, že o některých změnách se dozvíte v době, kdy je již SIPO uzavřené. Pamatujte si tedy tyto priority :
![]() Znovu
tedy zdůrazňuji: Chcete-li opravit předpis nějakého
vlastníka jednotky za nějaké období, provádějte to pokud
možno před kumulací do matrice a není-li to z nějakého
důvodu možné nebo vhodné, pak tedy opravnými větami
předpisu záloh - opravujete tak současně jednak předpis
záloh jako podklad pro zúčtování nákladů se zálohami,
jednak saldo !!!
Znovu
tedy zdůrazňuji: Chcete-li opravit předpis nějakého
vlastníka jednotky za nějaké období, provádějte to pokud
možno před kumulací do matrice a není-li to z nějakého
důvodu možné nebo vhodné, pak tedy opravnými větami
předpisu záloh - opravujete tak současně jednak předpis
záloh jako podklad pro zúčtování nákladů se zálohami,
jednak saldo !!!
Jak vidíte, většina dávkových operací souvisí s předáním změn na SIPO. Poslední dávkovou operací měsíce je vytvoření předpisů záloh na základě matrice (kumulace). Možná namítnete, že by bylo vhodnější zahrnout všechny měsíčně zpracovávané operace do jediné dávky, spouštěné jediným tlačítkem. Bylo by to skutečně vhodné kdyby neexistovaly velmi vážné důvody, proč to neudělat:
Vytvoření souborů změn však lze opakovat - vytvořené soubory jsou v podstatě kopiemi, a to až do potvrzení přijetí změnových souborů na SIPO. Vytvoření souborů změn a potvrzení jejich přijetí (resp.potvrzení zničení) jsou operace přepínající světla na pomyslném semaforu.