 |
|
Tomáš Vostrý, Sekce:Fyzika
Kinematika hmotného bodu
Mechanika je nejstarší obor fyziky, který zkoumá zákonitosti mechanického pohybu těles.
Mechanický pohyb - nejjednodušší forma pohybu, nastává pří přemísťování tělesa nebo jeho částí vzhledem k okolí. Součástí mechaniky je také kinematika.
Kinematika se zabývá pohybem těles, aniž by zkoumala, proč nastává.
Dynamika studuje příčiny pohybu těles a jejich pohybových změn.
Dělení mechaniky:
1. kinematika hmotného bodu
2. dynamika hmotného bodu
3. energie hmotného bodu a soustavy hmotných bodů
4. gravitační pole
5. mechanika tuhého tělesa
6. mechanika tekutin.
Kinematika hmotného bodu
Hmotný bod
- je myšlenkový model tělesa.
Vztažná soustava
- je soustava těles, ke kterým vztahujeme pohyb nebo klid sledovaného tělesa.
- nejčastěji volíme za vztažnou soustavu povrch Země nebo tělesa pevně spojená se Zemí (silnice)
Relativnost klidu a pohybu
Pohyb a klid těles je pouze relativní.
Absolutní klid neexistuje.
Pohyb je základní vlastností všech hmotných objektů.
Poloha hmotného bodu
- určujeme jí pomocí pravoúhlé soustavy souřadnic, spojenou se vztažnou soustavou.
- polohový vektor r - znázorňujeme orientovanou úsečkou, počáteční bod úsečky O umísťujeme do počátku soustavy souřadnic.
- velikost polohového vektoru r - se rovná vzdálenosti hmotného bodu od počátku souřadnic O.
Trajektorie hmotného bodu
- jde o geometrickou čáru, popisující všechny polohy, kterými hmotný bod prochází.
Dráha hmotného bodu
- je délka trajektorie, kterou bod opíše za určitý čas
- značí se: s
- jednotky: jednotky délky
Rychlost hmotného bodu
- průměrná rychlost: vp
- jde o skalár, definován podílem dráhy s a doby t, za níž bod dráhu urazí
- matematický vztah: 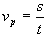
- jednotky: metr za sekundu m/s nebo m.s-1, kilometr za hodinu km/h km.h-1
- okamžitá rychlost - je vektor, určovaný pomocí změny polohového vektoru bodu.
- Matematický vztah: 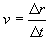 kde kde  je velmi malé je velmi malé
Zrychlení hmotného bodu
- zrychlení a je vektor, který se týká časové změny vektoru rychlosti.
- Matematický vztah: 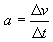 kde kde 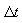 je velmi malé. je velmi malé.
Tečné a normálové zrychlení
- velikost tečného zrychlení = změna velikosti rychlosti
- velikost normálového zrychlení = změna směru rychlosti
- vztah: 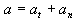
|
|
|
|
 |

