Even if the Mandelbrot-Set is perhaps the bestknown fractal in
the world, there is not much information on what it is and how to make it. In
this page I will try to make you understand the simple theory behind the
Mandelbrot-Set, and even show you a simple Pascal-program that calculates the
fractal. Hope you enjoy it!
Z(n) = (Z(n-1))2 + C
The problem is that the constant C and the function Z are
complex numbers.. (That is, they have a 'real' part (The numbers we normally
use) and an imaginary part (Numbers multiplied by the squareroot of -1,
represented by an 'i' after it) ). We use to say that C = a + bi
When
calculating the Mandelbrot-Set, you use the x-axis as the 'real' value, and the
y-axis as the 'imaginary' value.
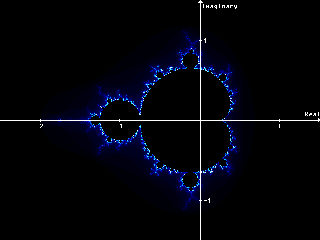 fig-1.1
fig-1.1FOR EACH pixel:
REPEAT
CALCULATE Z(n) = Z(n-1)^2 + C
iterations = iterations + 1
UNTIL value = infinite OR iterations > max_iterations
SET COLOR = iterations
The only problem above should be the calculation.. How do
we calculate the values ? How is this 'Z(n)'-function ???
As I
said, Z(n) = (Z(n-1))2 + C. In Mandelbrot-Set,
Z(0) = 0. That means:
Z(1) = C
Z(2) =
C2 + C
Z(3) = (C2 + C)2 + C and
so on..
I also said that C = a + bi. You then get:
Z(0) =
0
Z(1) = a + bi
Z(2) = (a + bi)2 + a +
bi
Z(3) = ((a + bi)2 + a + bi)2 + a + bi
.....
Now, all we have to do is test when Z(n) is infinite
:-)
The value of Z(n) is the length of the vector given by it's
real and imaginary parts. To calculate the length of a vector, we use the
formula
Length = Square-root of the value |a|2 + the value
|bi|2, or simply Length = SQRT(a2 + b2) (Note:
We can use the real value 'b' and not the imaginary value 'bi' here. We are just
interested in the value, not if it is real or imaginary)
So, when is the
length infinite ?
The bad news: You can't test if it is infinite..
The
good news: Whenever the length exceeds 2, you know that it (some day) -will- be
infinite !
To improve our 'program':
FOR EACH pixel:
REPEAT
CALCULATE Z(n) = Z(n-1)^2 + C
Length = Z(n).real^2 + Z(n).imaginary^2
iterations = iterations + 1
UNTIL Length > 4 OR iterations > max_iterations
SET COLOR = iterations
You might see that I test if the length exceeds 4, not 2, and
that I don't take the squareroot when calculating the length. As you all might
know, calculating the squareroot takes quite a lot of time, and when
SQRT('length') > 2, why not just test if 'length' > 4 ?!?
FUNCTION CALC_PIXEL(CA,CBi:REAL):INTEGER; {CA = real value, CBi = imaginary}
CONST MAX_ITERATION=128; {higher value -> better quality}
VAR
OLD_A :REAL; {just a variable to keep 'a' from being destroyed}
ITERATION :INTEGER; {the iteration-counter}
A,Bi :REAL; {function Z divided in real and imaginary parts}
LENGTH_Z :REAL; {length of Z, sqrt(length_z)>2 => Z->infinity}
BEGIN
A:=0; {initialize Z(0) = 0}
Bi:=0;
ITERATION:=0; {initialize iteration}
REPEAT
OLD_A:=A; {saves the 'a' (Will be destroyed in next line}
A:= A*A - B*B + CA;
B:= 2*OLD_A*B + CBi;
ITERATION := ITERATION + 1;
length_z:= a*a + b*b; {note: We do not perform the squareroot here}
UNTIL (length_z > 4) OR (iteration > max_iteration);
Calc_Pixel:=iteration;
END;
FOR y:= -1.25 TO 1.25 DO
FOR x:= -2 TO 1.25 DO
color:=CALC_PIXEL(x,y);
This 'program' would calculate the whole set, but you wouldn't be able to plot the Mandelbrot-set on the screen. That's why we use screen-coordinates, and calculate the C-value for each pixel: (assumes 640*480 VGA)
FOR y:= 0 TO 480-1 DO
FOR x:= 0 TO 640-1 DO
BEGIN
color:=CALC_PIXEL(real(x),imaginary(y));
PUTPIXEL(x,y,color);
END;
This 'program' would be able to plot the set, but it has to
compute the real and imaginary value for each pixel. How do we do that ???
PROGRAM Mandelbrot;
CONST MinX = -2;
MaxX = 1.25;
MinY = -1.25;
MaxY = 1.25;
[rest of program..]
When the upper left corner is supposed to be (MinX, MinY) , and the lower right corner is supposed to be (MaxX, MaxY), we get this formula:
real = MinX + x*(MaxX-MinX)/screenwidth; maginary = MinY + y*(MaxY-MinY)/screenheight;
Or, to save a lot of divisions (wich takes a lot of time..) :
dx = (MaxX-MinX)/screenwidth; {only needed to be done once !}
dy = (MaxY-MinY)/screenheight; {----------- "" --------------}
real = MinX + x*dx;
imaginary = MinY + y*dy;
Now we should be able to make a 'almost working' program
:-)
PROGRAM Mandelbrot;
CONST MinX = -2;
MaxX = 1.25;
MinY = -1.25;
MaxY = 1.25;
VAR dx, dy:REAL; {Don't confuse with 'real' numbers. This is the
Pascal Datatype REAL}
x, y :INTEGERS;
BEGIN
dx = (MaxX-MinX)/640;
dy = (Maxy-MinY)/480;
FOR y:=0 TO 480-1 DO
FOR x:=0 TO 640-1 DO
BEGIN
color:=CALC_PIXEL(MinX+x*dx, MinY+y*dy);
PUTPIXEL(x,y,color);
END;
END.
Because of the difference in initializing and using graphics on
different platforms, I can give you the complete Pascal source or complete C source for
IBM-Compatible machines with VGA-Cards, and people with UNIX-machines or those
lovely Amiga's have to make their own graphics-routines..
 The whole Mandelbrot-Set
The whole Mandelbrot-Set Figure 2
Figure 2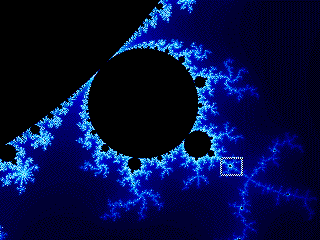 Figure 3
Figure 3 Figure 4
Figure 4